九年级(初三)数学下学期下册试题
下列两个变量x、y不是反比例的关系是( )
A . 书的单价为12元,售价y(元)与书的本数x(本)
B . xy=7
C . 当k=﹣1时,式子 中的y与x
D . 小亮上学用的时间x(分钟)与速度y(米/分钟)
中的y与x
D . 小亮上学用的时间x(分钟)与速度y(米/分钟)
 中的y与x
D . 小亮上学用的时间x(分钟)与速度y(米/分钟)
中的y与x
D . 小亮上学用的时间x(分钟)与速度y(米/分钟)
汽车超速行驶是交通安全的重大隐患,为了有效降低交通事故的发生,许多道路在事故易发路段设置了区间测速.如图,学校附近有一条笔直的公路  ,其间设有区间测速,所有车辆限速40千米/小时.数学实践活动小组设计了如下活动:在
,其间设有区间测速,所有车辆限速40千米/小时.数学实践活动小组设计了如下活动:在  上确定
上确定  两点,并在
两点,并在  路段进行区间测速,在
路段进行区间测速,在  外取一点P , 作
外取一点P , 作  ,垂足为点C.测得
,垂足为点C.测得  米,
米,  .
.
 ,其间设有区间测速,所有车辆限速40千米/小时.数学实践活动小组设计了如下活动:在
,其间设有区间测速,所有车辆限速40千米/小时.数学实践活动小组设计了如下活动:在  上确定
上确定  两点,并在
两点,并在  路段进行区间测速,在
路段进行区间测速,在  外取一点P , 作
外取一点P , 作  ,垂足为点C.测得
,垂足为点C.测得  米,
米,  .
. 
(参考数据:  )
)
-
(1) 求
 的长度;
的长度;
-
(2) 若测得一汽车从点A到点B用时6秒,请你用所学的数学知识说明该车是否超速.
如图,若△ABC内有一点P满足∠PAC=∠PCB,则点P为△ABC的布洛卡点,三角形的布洛卡点是法国数学教育家克洛尔于1816年首次发现,但他的发现并未被当时的人们所注意。1875年,布洛卡点被一个数学爱好者法国军官布洛卡重新发现,并用他的名字命名。问题:在等腰Rt△DEF中,∠EDF=90º,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ的值为( )

A . 5
B . 4
C . 3+  D . 2+
D . 2+ 
 D . 2+
D . 2+ 
如图是一个正方体的表面展开图,则原正方体中,与“安”字所在面相对的面上标的字是( )

A . 重
B . 泰
C . 山
D . 于
已知y与x-1成反比,并且当x=3时,y=4,则y与x之间的函数关系是( )
A . y=12(x-1)
B . y= C . y=12x
D . y=
C . y=12x
D . y=
 C . y=12x
D . y=
C . y=12x
D . y=
如图,已知,在锐角△ABC中,CE⊥AB于点E,点D在边AC上,联结BD交CE于点F,且EF·FC=FB·DF.

-
(1) 求证:BD⊥AC;
-
(2) 联结AF,求证:AF·BE=BC·EF.
如图,在平面直角坐标系中,已知点B的坐标为(﹣2,0),且OA=OC=4OB,抛物线y=ax2+bx+c(a≠0)图象经过A,B,C三点.

-
(1) 求A,C两点的坐标;
-
(2) 求抛物线的解析式;
-
(3) 若点P是直线AC下方的抛物线上的一个动点,作PD⊥AC于点D,当PD的值最大时,求此时点P的坐标及PD的最大值.
在Rt△ABC中,∠C=90°,AB=2,BC=  ,则sin
,则sin  =.
=.
 ,则sin
,则sin  =.
=.
如图是一个正方体的平面展开图,把展开图折叠成正方体后,“红”字的面的对面上的字是( )

A . 传
B . 因  C . 承
D . 基
C . 承
D . 基
 C . 承
D . 基
C . 承
D . 基
一个长方体的三视图如图,若其俯视图为正方形,则这个长方体的表面积为( )

A . 66
B . 48
C . 48 +36
D . 57
+36
D . 57
 +36
D . 57
+36
D . 57
如图1,一辆汽车从  地出发去往
地出发去往  地,
地,  ,
,  两地相距
两地相距  .由于
.由于  ,
,  之间某路段正在修路.驾驶员临时改变路线,先由
之间某路段正在修路.驾驶员临时改变路线,先由  地开往
地开往  地,再由
地,再由  地开往
地开往  地,如图2是从该场景中抽象出来的示意图,已知
地,如图2是从该场景中抽象出来的示意图,已知  ,
,  ,则这样的行驶路程比原来路程
,则这样的行驶路程比原来路程  远了多少?(结果精确到
远了多少?(结果精确到  ,参考数据:
,参考数据:  ,
, 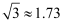 )
)
 地出发去往
地出发去往  地,
地,  ,
,  两地相距
两地相距  .由于
.由于  ,
,  之间某路段正在修路.驾驶员临时改变路线,先由
之间某路段正在修路.驾驶员临时改变路线,先由  地开往
地开往  地,再由
地,再由  地开往
地开往  地,如图2是从该场景中抽象出来的示意图,已知
地,如图2是从该场景中抽象出来的示意图,已知  ,
,  ,则这样的行驶路程比原来路程
,则这样的行驶路程比原来路程  远了多少?(结果精确到
远了多少?(结果精确到  ,参考数据:
,参考数据:  ,
, 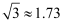 )
) 
如图1,⊙O的直径为BC,点A在⊙O上,∠BAC的平分线AD与BC交于点E,与⊙O交于点D, ,
,  .
.
 ,
,  .
. 
-
(1) 求
 .
.
-
(2) 求证:
 .
.
-
(3) 如图2,点F是AB延长线上一点,且
 . 求证:DF是⊙O的切线,并求线段DF的长.
. 求证:DF是⊙O的切线,并求线段DF的长.
如图,在  中,
中,  ,
,  ,
, 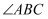 的平分线
的平分线  交
交  于点E,若
于点E,若  ,
,  ,则
,则  .
.
 中,
中,  ,
,  ,
, 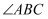 的平分线
的平分线  交
交  于点E,若
于点E,若  ,
,  ,则
,则  .
. 
计算:|3|+20180+4 sin45°- 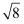
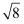
如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )

A .  =
=  B .
B .  =
=  C .
C .  =
=  D .
D .  =
= 
 =
=  B .
B .  =
=  C .
C .  =
=  D .
D .  =
= 
如图,P(12,a)在反比例函数  图象上,PH⊥x轴于H,则tan∠POH的值为.
图象上,PH⊥x轴于H,则tan∠POH的值为.
 图象上,PH⊥x轴于H,则tan∠POH的值为.
图象上,PH⊥x轴于H,则tan∠POH的值为.
-
(1) 计算:|-
 |-3tan60°+(2019-π)0
|-3tan60°+(2019-π)0
-
(2) 化简:(n-3)2+n(8-n)
已知点M (-2,3 )在双曲线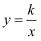 上,则下列各点一定在该双曲线上的是( )
上,则下列各点一定在该双曲线上的是( )
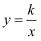 上,则下列各点一定在该双曲线上的是( )
上,则下列各点一定在该双曲线上的是( )
A . (3,-2 )
B . (-2,-3 )
C . (2,3)
D . (3,2)
下面四个图形每个均由六个相同的小正方形组成,折叠后能围成正方体的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,已知△PAB的三个顶点落在格点上.(注:每个小正方形的边长均为1).

-
(1) △PAB的面积为;
-
(2) 在图①中,仅用直尺画出一个以A为位似中心,与△PAB相似比为1:2的三角形;
-
(3) 在图①中,画一个以AB为边且面积为6的格点三角形ABC,符合条件的点C共个;
-
(4) 在图②中,只借助无刻度的直尺,在图中画出一个以AB为一边且面积为12的矩形ABMN.
最近更新
- 某一化石采集队,在甲、乙、丙三个不同的地层里挖掘到许多化石,记录如下:甲地层(恐龙蛋、始祖鸟、龟),乙地层(马、象牙、犀
- 16.人的胰岛素和胰蛋白酶的主要成分都是蛋白质,但合成这两种蛋白质的细胞的功能却完全不同,其根本原因是() A.不同细胞
- 下列各句中,加点成语的使用不恰当的一项是 ( ) A.哥本哈根联合国气候变
- 通过政府网站向群众开放政府的“红头文件”查阅,有利于( ) ①公民积极参与民主决策
- He seized me by the hand and _____ let me go. A. does no
- X、Y各代表一种物质,常温下,有某反应X+酸→盐+Y,其中X、Y的物质类别不可能是 A. 单质、单质 B. 盐、酸 C
- 阅读下面文章,完成以下题目 秋光里的黄金树 这里就正是秋天。 它辉煌的告别仪式正在山野间 河谷里轰轰烈烈地展开
- 为了进行Ⅰ项实验,请从Ⅱ项中选出一种试剂,从Ⅲ项中选出一种合适的实验操作方法,将标号填在后面的答案栏内。 Ⅰ实验Ⅱ试剂Ⅲ
- 你认为贫血的人体内有可能缺乏的无机盐是( ) A.镁 B.锌 C.铁 D.钙
- 体育课上,同学们分成两组进行足球比赛。球技高超的明扬却被两个组同时“拒之门外”,原因是在以往的比赛中,他总是训斥别人,嫌
- 读地球表面某区域的经纬网示意图,回答11-12题。11.M和N两点的实际距离约是 A.4444千米 B
- 体积为1.2×10-3 cm3的油滴在静止的水面上扩散为4 m2的单分子油膜,假设分子之间是紧密排列的,则可以估算出这种
- 下列能正确表示DNA片段的示意图是 (D)
- (08年昆明市适应考试文) 下列函数在为减函数的是(A) (B) (C) (D)
- 分解因式x3-6x2+9x=__________.
- 在探究功与速度变化的关系的实验中,下列说法中正确的是 (). A.长木板要适当倾斜,以平衡小车运动中受到的阻力 B.重复
- After a car accident put me into the hospital,I felt angry a
- 将下列词语依次填入各句横线处,最恰当的一组是 ①这些由园艺工人 培育的花卉,一定能把奥
- 已知:点O(0,0),A(1,2),B(4,5)及=+λ,试问:(1)λ为何值时,P在x轴上?在y轴上?在第二象限?
- 下列各组实验,不能达到实验目的的是 A.研究温度对化学反应的影响 B.研究CO2能否溶于水



