九年级(初三)数学下学期下册试题
放缩尺是一种绘图工具,它能把图形放大或缩小.

制作:把钻有若干等距小孔的四根直尺用螺栓分别在点A,B,C,D处连接起来,使得直尺可以绕着这些点转动,O为固定点, ,
,  , 在点A,E处分别装上画笔.
, 在点A,E处分别装上画笔.
画图:现有一图形M,画图时固定点O,控制点A处的笔尖沿图形M的轮廓线移动,此时点E处的画笔便画出了将图形M放大后的图形N.
原理:
连接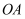 ,
,  , 可证得以下结论:
, 可证得以下结论:
① 和
和 为等腰三角形,则
为等腰三角形,则 ,
,  (180°-∠ ▲ );
(180°-∠ ▲ );
②四边形 为平行四边形(理由是 ▲ );
为平行四边形(理由是 ▲ );
③ , 于是可得O,A,E三点在一条直线上;
, 于是可得O,A,E三点在一条直线上;
④当 时,图形N是以点O为位似中心,把图形M放大为原来的 ▲ 倍得到的.
时,图形N是以点O为位似中心,把图形M放大为原来的 ▲ 倍得到的.
如图,在平面直角坐标系中,抛物线y=ax2+x的对称轴为x=2,顶点为A.点P为抛物线的对称轴上一点,连接OA、OP.当OA⊥OP时,点P的坐标为.

如图,某停车场人口的栏杆,从水平位置AB绕点O旋转到A'B′的位置已知AO=4m , 若栏杆的旋转角∠AOA′=50°时,栏杆A端升高的高度是( )

A .  B . 4sin50°
C .
B . 4sin50°
C .  D . 4cos50°
D . 4cos50°
 B . 4sin50°
C .
B . 4sin50°
C .  D . 4cos50°
D . 4cos50°
如图,已知点A在反比例函数y=  的图象上,点B在反比例函数y=
的图象上,点B在反比例函数y=  (k≠0)的图象上,AB∥x轴,分别过点A、B向x轴作垂线,垂足分别为C、D,若OC=
(k≠0)的图象上,AB∥x轴,分别过点A、B向x轴作垂线,垂足分别为C、D,若OC=  OD,则k的值为( )
OD,则k的值为( )
 的图象上,点B在反比例函数y=
的图象上,点B在反比例函数y=  (k≠0)的图象上,AB∥x轴,分别过点A、B向x轴作垂线,垂足分别为C、D,若OC=
(k≠0)的图象上,AB∥x轴,分别过点A、B向x轴作垂线,垂足分别为C、D,若OC=  OD,则k的值为( )
OD,则k的值为( ) 
A . 10
B . 12
C . 14
D . 16
已知点A(﹣2,y1),B(﹣1,y2)和C(3,y3)都在反比例函数y= 的图象上,则y1 , y2 , y3的大小关系为 . (用“<”连接)
的图象上,则y1 , y2 , y3的大小关系为 . (用“<”连接)
 的图象上,则y1 , y2 , y3的大小关系为 . (用“<”连接)
的图象上,则y1 , y2 , y3的大小关系为 . (用“<”连接)
反比例函数 的图象在( )
的图象在( )
 的图象在( )
的图象在( )
A . 第一、二象限
B . 第二、四象限
C . 第一、三象限
D . 第三、四象限
在我国古代数学名著《九章算术》中,将底面为矩形、一条侧棱垂直于底面的四棱锥称之为“阳马”(如图).“阳马”的俯视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,点 A 在双曲线y= 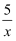 上,点 B 在双曲线y=
上,点 B 在双曲线y=  上,且AB∥x轴,则△OAB 的面积等于.
上,且AB∥x轴,则△OAB 的面积等于.
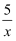 上,点 B 在双曲线y=
上,点 B 在双曲线y=  上,且AB∥x轴,则△OAB 的面积等于.
上,且AB∥x轴,则△OAB 的面积等于. 
如图,A、P、B、C是圆上的四点,∠APC =∠CPB = 60°, AP与CB的延长线相交于点D.

-
(1) 求证:△ABC是等边三角形;
-
(2) 若∠PAC= 90°,AB=
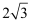 ,求PD的长.
,求PD的长.
如图,在平面直角坐标系中,直线y=  x+1与抛物线y=ax2+bx﹣3交于A,B两点,点A在x轴上,点B的纵坐标为3.点P是直线AB下方的抛物线上一动点(不与A,B重合),过点P作x轴的垂线交直线AB与点C,作PD⊥AB于点D
x+1与抛物线y=ax2+bx﹣3交于A,B两点,点A在x轴上,点B的纵坐标为3.点P是直线AB下方的抛物线上一动点(不与A,B重合),过点P作x轴的垂线交直线AB与点C,作PD⊥AB于点D

-
(1) ①求抛物线的解析式;②求sin∠ACP的值
-
(2) 设点P的横坐标为m
①用含m的代数式表示线段PD的长,并求出线段PD长的最大值;
②连接PB,线段PC把△PDB分成两个三角形,求出当这两个三角形面积之比为9:10时的m值;
③是否存在适合的m值,使△PCD与△PBD相似?若存在,直接写出m值;若不存在,说明理由.
1m长的标杆直立在水平地面上,它在阳光下的影子长度为0.8m,同一时刻,某电视塔的影子长度为100m,则该电视塔的高度为( )
A . 150m
B . 125m
C . 120m
D . 80m
如图,AB∥EF∥CD,AB=2,CD=8,AE:ED=1:5,则EF的长度为.

计算:2sin60°+| ﹣2|+
﹣2|+ .
.
 ﹣2|+
﹣2|+ .
.
如图所示,△ABC∽△ACD,且AB=10cm,AC=8cm,则AD的长是( )

A . 6.4cm
B . 6cm
C . 2cm
D . 4cm
如图,在5×4的正方形网格中,每个小正方形的边长均是1,△ABC的顶点均在小正方形的顶点上,则tanA的值为( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
风筝起源于中国,最早的风筝是由古代哲学家墨翟制造的,中国风筝问世后,很快被用于传递信息,飞跃险阻等军事需要,唐宋以后传入民间,成为人们休闲娱乐的玩具.上周末,小伟和爸爸一起去野外放风筝,不慎,两个风筝在空中P处缠绕在一起,如图,小伟在地面上的A处测得点P的仰角为30°,爸爸在距地面2米高的C处(即  米)测得点P的仰角为60°,已知A、B、D在一条直线上,
米)测得点P的仰角为60°,已知A、B、D在一条直线上,  ,
,  ,
,  米,求此时风筝P处距地面的高度PD.(结果保留根号)
米,求此时风筝P处距地面的高度PD.(结果保留根号)
 米)测得点P的仰角为60°,已知A、B、D在一条直线上,
米)测得点P的仰角为60°,已知A、B、D在一条直线上,  ,
,  ,
,  米,求此时风筝P处距地面的高度PD.(结果保留根号)
米,求此时风筝P处距地面的高度PD.(结果保留根号)

如图,晚上小亮在路灯下散步,在小亮由A处径直走到B处这一过程中,他在地上的影子( )

A . 逐渐变短
B . 先变短后变长
C . 先变长后变短
D . 逐渐变长
如图1,  中,
中,  ,
, 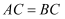 ,
,  为
为  的中线BD上的一点,将线段AE以E点为中心逆时针旋转90°得到线段EF , 恰EF经过点C .
的中线BD上的一点,将线段AE以E点为中心逆时针旋转90°得到线段EF , 恰EF经过点C .
 中,
中,  ,
, 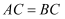 ,
,  为
为  的中线BD上的一点,将线段AE以E点为中心逆时针旋转90°得到线段EF , 恰EF经过点C .
的中线BD上的一点,将线段AE以E点为中心逆时针旋转90°得到线段EF , 恰EF经过点C . 
-
(1) 若
 ,则
,则  (用
(用  的代数式表示).
的代数式表示).
-
(2) 过点C作
 交AF于点H , 连接BH交EF于点G .
交AF于点H , 连接BH交EF于点G . ①求证:
 ;
;②若
 ,求EG的长.
,求EG的长.
下列几何体的主视图、左视图、俯视图都相同的是( )
A .  B .
B . 
C .
C .  D .
D . 
 B .
B . 
C .
C .  D .
D . 
如图,是某几何体的三视图,则该几何体的名称是( )

A . 圆柱
B . 圆锥
C . 棱柱
D . 长方体
最近更新
- Poorer children would be offered the chance to attend lesson
- 学校要围一个矩形花圃,花圃的一边利用足够长的墙,另三边用总长为36米的篱笆恰好围成(如图所示).设矩形的一边AB的长为x
- 电热饮水机是生活常用电器,小丽同学从说明书上了解到饮水机有加热和保温两种功能,可由机内温控开关S0进行自动控制,并给我们
- 阿长与《山海经》 我很愿意看看这样的图画,但不好意思力逼他去寻找,他是很疏懒的。问别人呢,谁也不肯真实地回答我。压岁钱还
- .下列事件中,必然事件是 A.抛掷1个均匀的骰子,出现6点向上 B.两直线被第三条直线所截,同位角 C.366人中至少有
- (1)水的电离平衡曲线如图所示,若A点表示25 ℃时水的电离达平衡时的离子浓度,B点表示100 ℃时水的电离达平衡时的
- Harryis ___________ my neighbour. He is a good friend of min
- 已知定义在R上的函数具有下列性质: ①;② (1)当n为定值时,记的表达式(k=0,1,2,…,n) (2)
- 海中两个灯塔A、B,其中B位于A的正东方向上,渔船跟踪鱼群由西向东航行,在点C处测得灯塔A在西北方向上,灯塔B在北偏东3
- 为切实保障受灾困难群众冬春期间基本生活,近期中央财政共安排2014—2015年冬春生活救助资金71亿元,第一批资金56.
- 从4名男生和3名女生中选出4人参加某个座谈会,若这4人中必须既有男生又有女生,则不同的选法种数共有______.(用数字
- 2011年5月,我国长江中下游部分地区遭遇大范围持续干旱。人民团结一致,共同抗旱。 (1)有些村庄打深井取用地下水。检验
- 依次填入下面一段文字横线处的语句,衔接最恰当的一组是(3分) “宰”一般人都知道, 其义为屠杀牲畜、家禽。那么“宰相”怎
- 材料一 有“军事奇才”、“常胜将军”之誉的刘伯承元帅,晚年拒看电视屏幕上的战争场景。他多次感慨道:“我们牺牲一位战士,
- 如图,在菱形中,点分别从点出发以同样的速度沿边,向点运动.给出以下四个结论:①;②;③当点分别为边的中点时,;④当点分别
- 根据图片信息,下列各项最符合20世纪50—70年代日本经济发展特征的是A.经济持续、高速增长B.20世纪70年代成为世界
- 基因敲除是应用DNA重组原理发展起来的一门新兴技术。通常意义上的基因敲除主要是应用DNA重组原理,用设计好的DNA片段替
- 2.下列各句中,没有语病的一句是()(3分) A.最新宣传片《大美开封》以全新的视角、唯美大气的制作风格,再现了古都昔日
- So long as teachers fail to distinguish between teaching and
- 下列项目中,在化学反应前后一定不改变的是 A.分子种类 B.原子数目 C.分子数目



