九年级(初三)数学下学期下册试题
计算:|3﹣π|﹣ 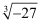 +
+  ×cos45°.
×cos45°.
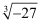 +
+  ×cos45°.
×cos45°.
如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且BC是⊙O的切线.

-
(1) 判断△CBP的形状,并说明理由;
-
(2) 若OA=6,OP=2,求CB的长;
-
(3) 设△AOP的面积是S1 , △BCP的面积是S2 , 且
 , 若⊙O的半径为6,BP=4
, 若⊙O的半径为6,BP=4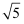 , 求tan∠APO.
, 求tan∠APO.
目前,我市正在积极创建文明城市,交通部门一再提醒司机:为了安全,请勿超速,并再进一步完善各类监测系统,如图,在某公路直线路段MN内限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据:  =1.41,
=1.41,  =1.73)
=1.73)
 =1.41,
=1.41,  =1.73)
=1.73) 
如图,数学活动小组为了测量学校旗杆AB的高度,使用长为2m的竹竿CD作为测量工具.移动竹竿,使竹竿顶端的影子与旗杆顶端的影子在地面O处重合,测得OD=4m , BD=14m , 则旗杆AB的高为m .

如图,在平面直角坐标系网格中,将△ABC进行位似变换得到△A1B1C1 .

-
(1) △A1B1C1与△ABC的位似比是;
-
(2) 画出△A1B1C1关于y轴对称的△A2B2C2;
-
(3) 设点P(a,b)为△ABC内一点,则依上述两次变换后,点P在△A2B2C2内的对应点P2的坐标是.
如图,则x=,y=.

如图1,直线l:  与x轴、y轴分别交于点A,B,点C
与x轴、y轴分别交于点A,B,点C  在直线l上,点P的坐标为(0,2),以点P为圆心,PC长为半径画⊙P.
在直线l上,点P的坐标为(0,2),以点P为圆心,PC长为半径画⊙P.

-
(1) 求直线l的解析式
-
(2) 求∠BAO的度数
-
(3) 判断直线l与⊙P的位置关系,并证明你的结论
-
(4) 如图2,点M(m,0),N(n,0)是x轴上的两个动点(点M在点N的左侧),且
 ,直线CM,CN与⊙P分别交于D,E,直线DE与x轴交于点Q,试探索∠DQM的大小是否变化,请说明理由。
,直线CM,CN与⊙P分别交于D,E,直线DE与x轴交于点Q,试探索∠DQM的大小是否变化,请说明理由。 
如图,四边形ABCD中, 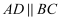 ,AC平分
,AC平分  ,BD平分
,BD平分 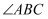 .
.
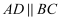 ,AC平分
,AC平分  ,BD平分
,BD平分 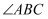 .
. 
-
(1) 如下图,求证:四边形ABCD是菱形;
-
(2) 如下图,点
 为四边形
为四边形  外一点,连接
外一点,连接  、
、 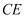 、
、  ,
,  交
交  于点
于点  ,
,  ,求证:
,求证:  ;
;
-
(3) 如下图,在(2)的条件下,
 ,点
,点  为
为  上一点,连接
上一点,连接  ,点
,点  为
为  延长线上一点,
延长线上一点,  ,连接
,连接  ,
,  为
为  上一点,连接
上一点,连接  ,若
,若  ,求
,求  的值.
的值.
花园小区有一朝向为正南方向的居民楼(如图),该居民楼的一楼是高4米的小区商场,商场以上是居民住房.在该楼的前面16米处要盖一栋高18米的办公楼.当冬季正午的阳光与水平线的夹角为 时,问:
时,问:
 时,问:
时,问:
-
(1) 商场以上的居民住房采光是否有影响,为什么?
-
(2) 若要使商场采光不受影响,两楼应相距多少 米?(结果保留一位小数)
(参考数据:
 ,
,  ,
,  )
)
如图,在△ABC中,点D、E分AB、AC边上,DE∥BC,若AD:AB=3:4,AE=6,则AC等于( )


A . 3
B . 4
C . 6
D . 8
在  中,
中,  ,
,  ,则( )
,则( )
 中,
中,  ,
,  ,则( )
,则( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,直线y=x+2与双曲线y= 相交于点A,点A的纵坐标为3,k的值为( ).
相交于点A,点A的纵坐标为3,k的值为( ).

A . 1
B . 2
C . 3
D . 4
如图,已知△ABC的外接圆⊙O的半径为3,AC=4,则sinB的值是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在一次户外综合实践活动中,九年级数学兴趣小组用无人机航拍测量公园内一条笔直的骑行步道AB的长度.由于无人机控制距离有限,为了安全,不能直接测量,他们采用如下方法:如图,在起点A的正上方点C处测得终点B的俯角α=17.1°;接着无人机往终点B方向水平飞行0.9km到达点D处, 此时测得终点B的俯角β=45°.求骑行步道AB的长度.(结果精确到0.1km,参考数据:sin17.1°≈0.29,cos17.1°≈0.96,tan17.1°≈0.31, )
)
 )
) 
“新中梁山隧道”于2017年11月21日开放通行,原中梁山隧道将封闭升级,扩容改造工程预计2018年3月全部完工,届时将实现双向8车道通行,隧道通行能力将增加一倍,沿线交通拥堵状况将有所缓解.图中线段AB表示该工程的部分隧道.无人勘测机从隧道侧的A点出发时,测得C点正上方的E点的仰角为45°,无人机飞行到E点后,沿着坡度i=1:3的路线EB飞行,飞行到D点正上方的F点时,测得A点的俯角为12°,其中EC=100米,A,B,C,D,E,F在同一平面内,则隧道AD段的长度约为( )米,(参考数据:tan12°≈0.2,cosl2°≈0.98)

A . 200
B . 250
C . 300
D . 540
如图,平行四边形ABCD,E是BC上一点,BE:EC=2:3,AE交BD于F,则BF:FD等于( )

A . 2:5
B . 3:5
C . 2:3
D . 5:7
如图,C是圆O被直径AB分成的半圆上一点,过点C的圆O的切线交AB的延长线于点P,连接CA,CO,CB.

-
(1) 求证:∠ACO=∠BCP;
-
(2) 若∠ABC=2∠BCP,求∠P的度数;
-
(3) 在(2)的条件下,若AB=4,求图中阴影部分的面积(结果保留π和根号).
如图,反比例函数  的图象大致是( )
的图象大致是( )
 的图象大致是( )
的图象大致是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知反比例函数  的图象位于第一、三象限,则
的图象位于第一、三象限,则  的取值范围是.
的取值范围是.
 的图象位于第一、三象限,则
的图象位于第一、三象限,则  的取值范围是.
的取值范围是.
在△ABC中,点D、E分别在边BA、CA的延长线上,下列比例式中能判定DE∥BC的为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
最近更新
- 如图是油路管道的一部分,延伸外围的支路恰好构成一个直角三角形,两直角边分别为3m和4m.。按照输油中心O到三条支路的距离
- . 设函数,且,,则下列结论中不正确的k*s#5^u是 A. C. D.
- 右图是KNO3和NaCl的溶解度曲线。下列说法中正确的是:( ) A.NaCl的溶解度不受温度的影响 B
- 已知双曲线C:-=1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为( ) A.-=1 B.-=
- 孔子曰:三人行,必有我师焉,择其善者而从之,择其不善者而改之。孔子对知识的态度体现的哲理是 ①一分为二
- 如图甲所示,建立Oxy坐标系。两平行极板P、Q垂直于y轴且关于x轴对称,极板长度和板间距均为l。在第一、四象限有磁感应强
- Every artist knows in his heart that he is saying something
- 北京时间2010年10月1日长征三号丙火箭在位于中国四川的西昌卫星发射中心发发射,把嫦娥二号探月卫星成功送入太空。“嫦娥
- 2009年世界环境日主题是“地球需要你:团结起来应对气候变化”。 (1)有人认为,天然气作燃料可避免温室效应的发生。你
- 下列关于声音的说法正确的是( ) A、只要物体振动就可以听到声音 B、只要听到声音物体一
- 阅读下面语段,按要求回答问题: 对别人文章的理解必须全面,( ),很可能歪曲本意。 A. 生吞活剥 B. 寻章摘句 C.
- 为解决当前稀土等矿产勘查开采中存在的突出问题,国土资源部决定在2010年6月至11月开展稀土等矿产开发秩序专项整治行动,
- 已知. (1)求函数的定义域; (2)判断函数的奇偶性; (3)求的值.
- 直升机悬停在空中向地面投放装有救灾物资的箱子,如图所示.设投放初速度为零,箱子所受的空气阻力与箱子下落速度的平方成正比,
- By working hard and never giving up,you are_________to be s
- 春秋战国时期,以家庭为单位的个体小农经济得以初步发展的主要条件包括 ( ) ①铁
- 已知常温下的醋酸铵溶液呈中性,下列叙述正确的是A.醋酸铵溶液中水的电离程度与纯水相同B.由醋酸铵溶液呈中性可推知NH4H
- 完成下列小题(14分) (1)右图是某有机物结构简式, 按系统命名法,该有机物的名称是 。 (2)主链含5个
- 对于反应 3 Cu+ 8 HNO3 = 3 Cu(NO3)2 + 2NO↑+ 4H2O,以下叙述正确的是( ) A.氧化
- 化学就在我们身边。通过一年的学习,让我们共同分享同学们的收获。 (1)写出一种你最熟悉的元素① ,它属于 ②(填“金属”



