九年级(初三)数学下学期下册试题
一个圆锥的底面半径为  ,母线长为
,母线长为  ,这个圆锥的侧面积为( )
,这个圆锥的侧面积为( )
 ,母线长为
,母线长为  ,这个圆锥的侧面积为( )
,这个圆锥的侧面积为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图所示的几何体的俯视图可能是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在四边形ABCD中, , 对角线AC、BD相交于点E,
, 对角线AC、BD相交于点E, ,
,  , 若
, 若 , 则
, 则 的长为.
的长为.
 , 对角线AC、BD相交于点E,
, 对角线AC、BD相交于点E, ,
,  , 若
, 若 , 则
, 则 的长为.
的长为.
已知:如图,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB,AC相交于D点,双曲线y=  (x>0)经过D点,交BC的延长线于E点,且OB•AC=160,有下列四个结论:①双曲线的解析式为y=
(x>0)经过D点,交BC的延长线于E点,且OB•AC=160,有下列四个结论:①双曲线的解析式为y=  (x>0);②E点的坐标是(4,8);③sin∠COA=
(x>0);②E点的坐标是(4,8);③sin∠COA=  ;④AC+OB=12
;④AC+OB=12  ,其中正确的结论有( )
,其中正确的结论有( )
 (x>0)经过D点,交BC的延长线于E点,且OB•AC=160,有下列四个结论:①双曲线的解析式为y=
(x>0)经过D点,交BC的延长线于E点,且OB•AC=160,有下列四个结论:①双曲线的解析式为y=  (x>0);②E点的坐标是(4,8);③sin∠COA=
(x>0);②E点的坐标是(4,8);③sin∠COA=  ;④AC+OB=12
;④AC+OB=12  ,其中正确的结论有( )
,其中正确的结论有( )

A . 1个
B . 2个
C . 3个
D . 4个
如图,将边长为  的正方形ABCD绕点A逆时针方向旋转30o后得到正方形
的正方形ABCD绕点A逆时针方向旋转30o后得到正方形  ,则图中阴影部分的面积为 平方单位.
,则图中阴影部分的面积为 平方单位.
 的正方形ABCD绕点A逆时针方向旋转30o后得到正方形
的正方形ABCD绕点A逆时针方向旋转30o后得到正方形  ,则图中阴影部分的面积为 平方单位.
,则图中阴影部分的面积为 平方单位. 
如图所示,已知在三角形纸片ABC中,BC=3,AB=6,∠BCA=90°.在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( )
A . 6
B . 3
C . 2
 D .
D . 

 D .
D . 
如图,已知P是射线OB上的任意一点,PM⊥OA于M,且 ,则cosα的值等于( )
,则cosα的值等于( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在平面直角坐标系xOy中,直线AB与x轴、y轴分别交于点A,B,与反比例函数y= (k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若
(k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若 (m为大于1的常数).记△CEF的面积为S1 , △OEF的面积为S2 , 求
(m为大于1的常数).记△CEF的面积为S1 , △OEF的面积为S2 , 求 的值. (用含m的代数式表示)
的值. (用含m的代数式表示)

如图,在平面直角坐标系中,函数  (x>0,常数k>0)的图象经过点A(1,2)、B(m,n)(m>1).过点B作y轴的垂线,垂足为C若△ABC的面积为2,则点B的坐标为.
(x>0,常数k>0)的图象经过点A(1,2)、B(m,n)(m>1).过点B作y轴的垂线,垂足为C若△ABC的面积为2,则点B的坐标为.
 (x>0,常数k>0)的图象经过点A(1,2)、B(m,n)(m>1).过点B作y轴的垂线,垂足为C若△ABC的面积为2,则点B的坐标为.
(x>0,常数k>0)的图象经过点A(1,2)、B(m,n)(m>1).过点B作y轴的垂线,垂足为C若△ABC的面积为2,则点B的坐标为.
在我们学习过的数学教科书中,有一个数学活动,若身旁没有量角器或三角尺,又需要作  等大小的角,可以采用如下方法:
等大小的角,可以采用如下方法:
 等大小的角,可以采用如下方法:
等大小的角,可以采用如下方法:

操作感知:
第一步:对折矩形纸片  ,使
,使  与
与  重合,得到折痕
重合,得到折痕  ,把纸片展开(如图13-1).
,把纸片展开(如图13-1).
第二步:再一次折叠纸片,使点  落在
落在  上,并使折痕经过点
上,并使折痕经过点  ,得到折痕
,得到折痕  ,同时得到线段
,同时得到线段  (如图13-2).
(如图13-2).
-
(1) 猜想论证:
若延长 交
交  于点
于点  ,如图13-3所示,试判定
,如图13-3所示,试判定  的形状,并证明你的结论.
的形状,并证明你的结论.
-
(2) 拓展探究:
在图13-3中,若 ,当
,当  满足什么关系时,才能在矩形纸片
满足什么关系时,才能在矩形纸片  中剪出符(1)中的等边三角形
中剪出符(1)中的等边三角形  ?
?
如图是三角尺在灯泡O的照射下在墙上形成的影子.现测得  ,
,  ,则这个三角尺的周长与它在墙上形成的影子的周长之比是.
,则这个三角尺的周长与它在墙上形成的影子的周长之比是.
 ,
,  ,则这个三角尺的周长与它在墙上形成的影子的周长之比是.
,则这个三角尺的周长与它在墙上形成的影子的周长之比是.
如图是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据求得这个几何体的侧面积是cm2.

如图,某海滨浴场岸边可近似地看成直线,位于岸边A处的救生员发现海中B处有人求救,1号救生员以6m/秒的速度从A处跑300米到距离B最近的D处,然后游向B处.他在海中游进的速度为2m/秒,∠BAD=45°.
(1)根据以上条件分析1号救伤员的选择是否有道理,并说明理由.
(2)若2号救生员跑到C处,再游向B处,且∠BCD=65°,问:哪名救生员先赶到B处救人?(参考数据:sin65°≈0.9,cos65°≈0.4,tan65°≈2.1, ≈1.4,且为计算方便,计算过程中均保留1位小数)
≈1.4,且为计算方便,计算过程中均保留1位小数)

如图、在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(4,1),B(2,3),C(1,2).

⑴画出与△ABC关于y轴对称的△A1B1C1;
⑵以原点O为位似中心,在第三象限内画一个△A2B2C2 , 使它与△ABC的相似比为 , 并写出点B2的坐标.
, 并写出点B2的坐标.
如图,是由若干个相同的小正方形搭成的一个几何体的主视图和左视图,则组成这个几何体的小正方形的个数不可能是( )

A . 3
B . 4
C . 5
D . 6
已知点(m﹣1,y1),(m﹣3,y2)是反比例函数y=  (m<0)图象上的两点,则y1y2(填“>”或“=”或“<”)
(m<0)图象上的两点,则y1y2(填“>”或“=”或“<”)
 (m<0)图象上的两点,则y1y2(填“>”或“=”或“<”)
(m<0)图象上的两点,则y1y2(填“>”或“=”或“<”)
某几何体的三视图如图所示,则该几何体是( )

A . 正方体
B . 长方体
C . 三棱柱
D . 三棱锥
如图,一艘船从A港沿东南方向航行到C港,然后沿南偏西30°方向航行到B港,此时A港恰好在B港的正北方向,且距离A港30nmile.求B,C两港之间的距离.(结果保留整数,参考数据  )
)
 )
) 
如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且BC是⊙O的切线,

-
(1) 求证:CE=CB;
-
(2) 连接AF,BF,求tan∠ABF;
-
(3) 如果CD=15,BE=10,sinA=
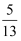 ,求⊙O的半径.
,求⊙O的半径.
-
(1) 计算:2﹣1+2cos30°+(π﹣3.14)0﹣
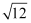 .
.
-
(2) 先化简,再求值:
 ﹣
﹣  ,其中x=﹣2.
,其中x=﹣2.
最近更新
- 纸币是由国家发行的强制使用的,这就是说( ) ①在一定时期内发行多少纸币是由国家决定 ②纸币的面额(如1元.10元.
- 下列选项中,属于动植物细胞共有的糖类的是( ) A.葡萄糖、淀粉、果糖 B.葡萄糖、核
- 同温同压下,在四支相同体积的试管中分别充有等体积混合的两种气体,它们是①NO和NO2 ②NO2和O2 ③NH3和N2
- 如图所示,在一固定的竖直光滑圆弧轨道内部的最低点,静止有一个可视为质点的小球,已知地球表面的重力加速度为g, 圆弧轨道的
- 写出下列反应的化学方程式: ⑴氢氧化钠溶液与硫酸铜溶液反应______________________________;
- 点P从(1,0)出发,沿单位圆x2+y2=1按逆时针方向运动弧长到达Q点,则Q的坐标为( )A.(-,)
- 第三节 Find Yourself Sometimes taking a step back from yourdai
- 2008年春节前,中国十几个省份遭受了50年不遇的冰雪灾害。假如 你是李华,你的国外朋友Steve发来电子邮件向你了解受
- 二战后初期,美国总统杜鲁门提出公平施政的政策纲领,其主要举措有:扩大社会保险范围,提高最低工资限额;提倡国民健康保险;建
- — Excuse me. ________did you say you'd like to do, Miss Kilp
- (每空2分,共10分) 四川汶川盛产品质优良的甜樱桃。甜樱桃中含有一种羟基酸(用A表示)。A的碳链结构无支链,化学式
- 下列地区,地形具有“山河相间、纵列分布”特点的是( ) A.中南半岛 B.日本群岛
- 根据句子所给单词的首字母或中文意思,在答题纸上按题号写出各词正确的形式。 1.His excellent work i_
- 如图所示的四条纸带,是某同学练习使用打点计时器得到的纸带(纸带的右端后通过打点计时器).从点痕的分布情况可以断定,纸带
- 物质之间发生化学反应时,一定发生变化的是( ) A.颜色 B.状态
- ________ it is good for us to surf the Internet depends on _
- 2009年是我国改革开放31周年。改革开放以来,我国农民有三个伟大创造:一是实行家庭承包责任制;二是乡镇企业异军突起;三
- 某地区有一口150米深的矿井,采矿工人发现在井底每年能见到两次阳光,此井最有可能位于
- 人感知声音的基本过程是这样的:外界传来的声音引起______振动,这种振动经过__________及其他组织传给____
- 下列关于酶的叙述,正确的是() ①酶是活细胞产生的 ②酶都有消化功能 ③蛋白质都是酶 ④酶具有多样性 ⑤酶可促进反应,与



