九年级(初三)数学下学期下册试题
对于钝角α,定义它的三角函数数值如下:
sinα=sin(180°﹣α),cosα=﹣cos(180°﹣α).
-
(1) 求sin135°,cos150°的值;
-
(2) 若一个三角形的三个内角的比为1:1:4,A,B是这个三角形的两个顶点,且∠A≤∠B,sinA,cosB是方程4x2﹣mx﹣1=0的两个不相等的实数根,求m值及∠A,∠B的大小.
如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB、CD分别表示一楼、二楼地面的水平线,电梯坡面BC的坡度i=1:  ,则电梯坡面BC的坡角α为( )
,则电梯坡面BC的坡角α为( )
 ,则电梯坡面BC的坡角α为( )
,则电梯坡面BC的坡角α为( ) 
A . 15°
B . 30°
C . 45°
D . 60°
计算:tan260°﹣2cos60°﹣  sin45°+6cos30°-
sin45°+6cos30°- 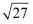 +
+ 
 sin45°+6cos30°-
sin45°+6cos30°- 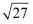 +
+ 
如图,小明在学校门口的点C处测得树的顶端A仰角为α,同时测得  ,则树的高度
,则树的高度  为( )
为( )
 ,则树的高度
,则树的高度  为( )
为( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
点P(1,3)在反比例函数y=  (k≠﹣1)图象上,则k=.
(k≠﹣1)图象上,则k=.
 (k≠﹣1)图象上,则k=.
(k≠﹣1)图象上,则k=.
下列图形中,是圆锥的侧面展开图的为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,已知A(3,0),B(2,3),将△OAB以点O为位似中心,相似比为2:1,放大得到△OA′B′,则顶点B的对应点B′的坐标为.

某公司计划投资300万元引进一条汽车配件流水生产线,经过调研知道该流水生产线的年产量为1040件,每件总成本为0.6万元,每件出厂价0.65万元;流水生产线投产后,从第1年到第n年的维修、保养费用累计y(万元)如下表:
|
第 | | | | | | | ··· |
| 维修、保养费用累计 | | | | | | | ··· |
若上表中第n年的维修、保养费用累计y(万元)与n的数量关系符合我们已经学过的一次函数、二次函数、反比例函数中某一个.
-
(1) 求出y关于n的函数解析式;
-
(2) 投产第几年该公司可收回
 万元的投资?
万元的投资?
-
(3) 投产多少年后,该流水线要报废(规定当年的盈利不大于维修、保养费用累计即报费)?
下列四条线段不成比例的是( )
A . a=3,b=6,c=2,d=4
B . a=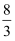 ,b=8,c=5,d=15
C . a=
,b=8,c=5,d=15
C . a= ,b=2,c=3,d=
,b=2,c=3,d= D . a=1,b=
D . a=1,b= ,c=
,c= ,d=
,d=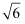
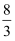 ,b=8,c=5,d=15
C . a=
,b=8,c=5,d=15
C . a= ,b=2,c=3,d=
,b=2,c=3,d= D . a=1,b=
D . a=1,b= ,c=
,c= ,d=
,d=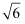
如图,射线PO与⊙O交于A、B两点,PC、PD分别与⊙O相切于点C、D.

-
(1) 请写出两个正确结论;
-
(2) 若PD=6,∠CPO=30°,求⊙O的半径.
如图,在Rt△ABC中,∠C=90°,AB=6,cosB=  ,则BC的长为.
,则BC的长为.
 ,则BC的长为.
,则BC的长为. 
计算: 

如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为i=1:0.75、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)( )

A . 21.7米
B . 22.4米
C . 27.4米
D . 28.8米
已知点(﹣2,y1),(﹣1,y2),(1,y3)都在反比例函数y= 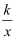 (k<0)的图象上,那么y1 , y2与y3的大小关系是( )
(k<0)的图象上,那么y1 , y2与y3的大小关系是( )
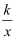 (k<0)的图象上,那么y1 , y2与y3的大小关系是( )
(k<0)的图象上,那么y1 , y2与y3的大小关系是( )
A . y3<y1<y2
B . y3<y2<y1
C . y1<y2<y3
D . y1<y3<y2
下列关系式中,哪个等式表示 是
是 的反比例函数( )
的反比例函数( )
 是
是 的反比例函数( )
的反比例函数( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在△ABC中,DE∥BC,若AD=1,DB=2,则 的值为.
的值为.
 的值为.
的值为.
如图,小明从左面看在水平讲台上放置的圆柱形水杯和长方体形粉笔盒看到的是 




A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D .
已知点A(a,y1),B(a+1,y2)在反比例函数y (m是常数)的图象上,且y1>y2 , 则a的取值范围是.
(m是常数)的图象上,且y1>y2 , 则a的取值范围是.
 (m是常数)的图象上,且y1>y2 , 则a的取值范围是.
(m是常数)的图象上,且y1>y2 , 则a的取值范围是.
图甲,乙都是由小立方体组成的几何体,则图甲、图乙的视图一样的是( )
A . 主视图、左视图
B . 主视图、俯视图
C . 左视图、俯视图
D . 以上都不对
如图是一个正方体的平面展开图,正方体中相对的面上的数字或代数式互为相反数,则2x+3y的值为.

最近更新
- The people of New Orleans need to know they are not ____, an
- 饮食结构不合理又可能引起维生素缺乏症。如果某成年人的体内长期缺乏维生素A和维生素D,那么此人就会患( ) A.角膜炎,
- Allen goes everywhere with Brigitta Anderson, a54 year-old s
- 爸爸奖 (1)书架高处,放着一只纸箱。每当我伏案写作,就能看到它,箱子里是些私人收藏,
- 在生命系统的各个层次中,能完整地表现各种生命活动最微小的层次是A.原子 B.分子
- 第二次世界大战后,战时的合作也不再持续,世界进入了以美国和苏联为首的两极格局,冷战开始的标志是 () A.丘吉尔发表“铁
- (本题满分12分) 已知函数,其中为大于零的常数.(1)若函数在上单调递增,求的取值范围;(2)求函数在区间上的最小值;
- 下面是关于-1.5这个数在数轴上的位置的描述,其中正确的是 ( ) A.在-左边 B.在+0.1的右边
- 植物生长素的化学成分是( ) A.吲哚乙酸 B.丙酮酸 C.氨基酸 D
- 马克思说:“在美国历史上和人类历史上,林肯必将与华盛顿齐名。”马克思如此高度评价林肯,是因为林肯政府 A.巩固了北方工业
- —Could you tell me hecame here? —He drove here him
- 依次填人下面一段文字横线处的语句,衔接最恰当的一组是 驱车从五家渠市出发,沿着古尔班通古特沙漠南缘一路向东,经吉木萨尔和
- ________ that I was puzzled. A.So difficult a question did h
- 质量为4千克的物体只受两个共点力的作用,其中一个力的方向可以任意改变,这两个力的大小分别为5牛和7牛(不受其它力)。那么
- 下图是同学们经常使用的铅笔示意图。(1)在组成铅笔的各种材料中,能导电的是 ,含有有机物的是
- 孔子提出“畏天命”的观点,说“获罪于天,无所祷也”。这是属于( ) A.机械唯物主义观点
- 通式为CnH2n-2的一种气态烃完全燃烧后生成CO2和H2O的物质的量之比为4∶3,这种烃的链状同分异构体有( )
- 如图所示,在光滑绝缘水平面上,有一铝球以一定的初速度通过有界匀强磁场,则从球开始进入磁场到完全穿出磁场过程中(磁场宽度大
- 唐代诗人白居易说过:“天育物有时,地生财有限,而人之欲无极。以有时有限奉无极之欲,而法制不生期间,则必物暴殄而财乏用矣。
- 食品安全与健康密切相关。下列做法不会危及人体健康的是A.用甲醛溶液浸泡水产品延长保存期B.在酱油中加入铁强化剂以补充铁元
 年
年