九年级(初三)数学下学期下册试题
如图是一个正方体的表面展开图,则原正方体中与“建”字所在面的相对面上标的字是( )

A . 美
B . 丽
C . 镇
D . 海
如图是一个立体图形的三视图,请根据视图写出该立体图形的名称,并计算该立体图形的体积(结果保留π).

如图,将边长为6的等边△ABC放置在平面直角坐标系中,则A点坐标为.

小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,这样就可以求出67.5°角的正切值是( )
A .  +1
B .
+1
B .  +1
C . 2.5
D .
+1
C . 2.5
D . 
 +1
B .
+1
B .  +1
C . 2.5
D .
+1
C . 2.5
D . 
如图,直线AC与反比例函数y= (k>0)的图像相交于A、C两点,与x轴交于点D,过点D作DE⊥x轴交反比例函y=
(k>0)的图像相交于A、C两点,与x轴交于点D,过点D作DE⊥x轴交反比例函y= (k>0)的图像于点E,连结CE,点B为y轴上一点,满足AB=AC,且BC恰好平行于x轴.若S△DCE=1,则k的值为.
(k>0)的图像于点E,连结CE,点B为y轴上一点,满足AB=AC,且BC恰好平行于x轴.若S△DCE=1,则k的值为.
 (k>0)的图像相交于A、C两点,与x轴交于点D,过点D作DE⊥x轴交反比例函y=
(k>0)的图像相交于A、C两点,与x轴交于点D,过点D作DE⊥x轴交反比例函y= (k>0)的图像于点E,连结CE,点B为y轴上一点,满足AB=AC,且BC恰好平行于x轴.若S△DCE=1,则k的值为.
(k>0)的图像于点E,连结CE,点B为y轴上一点,满足AB=AC,且BC恰好平行于x轴.若S△DCE=1,则k的值为.

筒车是我国古代利用水力驱动的灌溉工具,车轮缚以竹简,旋转时低则舀水,高则泻水.如图,水力驱动筒车按逆时针方向转动,竹筒把水引至A处,水沿射线 方向泻至水渠
方向泻至水渠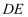 , 水渠
, 水渠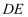 所在直线与水面
所在直线与水面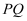 平行;设筒车为
平行;设筒车为 ,
,  与直线
与直线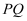 交于P,Q两点,与直线
交于P,Q两点,与直线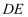 交于B,C两点,恰有
交于B,C两点,恰有 , 连接
, 连接 .
.
 方向泻至水渠
方向泻至水渠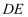 , 水渠
, 水渠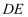 所在直线与水面
所在直线与水面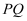 平行;设筒车为
平行;设筒车为 ,
,  与直线
与直线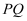 交于P,Q两点,与直线
交于P,Q两点,与直线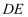 交于B,C两点,恰有
交于B,C两点,恰有 , 连接
, 连接 .
. 

-
(1) 求证:
 为
为 的切线;
的切线;
-
(2) 筒车的半径为
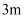 ,
,  . 当水面上升,A,O,Q三点恰好共线时,求筒车在水面下的最大深度(精确到
. 当水面上升,A,O,Q三点恰好共线时,求筒车在水面下的最大深度(精确到 , 参考值:
, 参考值: ).
).
如图,在正方形ABCD中,AB=4,P是BC边上一动点(不含B,C两点),将△ABP沿直线AP翻折,点B落在点E处,在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.

-
(1) 发现:
△CMP和△BPA是否相似,若相似给出证明,若不相似说明理由;
-
(2) 思考:
线段AM是否存在最小值?若存在求出这个最小值,若不存在,说明理由;
-
(3) 探究:
当△ABP≌△ADN时,求BP的值是多少?
如图是一个用于防震的L形的包装用泡沫塑料,当俯视它时看到的图形形状是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,  ,点
,点  分别在
分别在  上,如果
上,如果  ,那么
,那么  的长为.
的长为.
 ,点
,点  分别在
分别在  上,如果
上,如果  ,那么
,那么  的长为.
的长为. 
如图,在平面直角坐标系中,点A在一次函数  位于第一象限的图象上运动,点B在x轴正半轴上运动,在AB右侧以它为边作矩形ABCD , 且
位于第一象限的图象上运动,点B在x轴正半轴上运动,在AB右侧以它为边作矩形ABCD , 且  ,
,  ,则OD的最大值是.
,则OD的最大值是.
 位于第一象限的图象上运动,点B在x轴正半轴上运动,在AB右侧以它为边作矩形ABCD , 且
位于第一象限的图象上运动,点B在x轴正半轴上运动,在AB右侧以它为边作矩形ABCD , 且  ,
,  ,则OD的最大值是.
,则OD的最大值是. 
两个相似三角形的面积比是9:16,则这两个三角形的相似比是( )
A . 9︰16
B . 3︰4
C . 9︰4
D . 3︰16
如图,为了测量山脚到塔顶的高度(即  的长),某同学在山脚A处用测角仪测得塔顶D的仰角为
的长),某同学在山脚A处用测角仪测得塔顶D的仰角为  ,再沿坡度为
,再沿坡度为  的小山坡前进400米到达点B,在B处测得塔顶D的仰角为
的小山坡前进400米到达点B,在B处测得塔顶D的仰角为  .
.
 的长),某同学在山脚A处用测角仪测得塔顶D的仰角为
的长),某同学在山脚A处用测角仪测得塔顶D的仰角为  ,再沿坡度为
,再沿坡度为  的小山坡前进400米到达点B,在B处测得塔顶D的仰角为
的小山坡前进400米到达点B,在B处测得塔顶D的仰角为  .
. 
-
(1) 求坡面
 的铅垂高度(即
的铅垂高度(即  的长);
的长);
-
(2) 求
 的长.(结果保留根号,测角仪的高度忽略不计).
的长.(结果保留根号,测角仪的高度忽略不计).
如图,原点  是
是  和
和  的位似中心,点
的位似中心,点  与点
与点  是对应点,
是对应点,  的面积是
的面积是  ,则
,则  的面积是.
的面积是.
 是
是  和
和  的位似中心,点
的位似中心,点  与点
与点  是对应点,
是对应点,  的面积是
的面积是  ,则
,则  的面积是.
的面积是.
如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,D,E,F分别是OA,OB,OC的中点,则△DEF与△ABC的面积比是( )
A . 1∶6
B . 1∶5
C . 1∶4
D . 1∶2
已知函数y= ,当x≥-1时,y的取值范围是( )
,当x≥-1时,y的取值范围是( )
 ,当x≥-1时,y的取值范围是( )
,当x≥-1时,y的取值范围是( )
A . y<-1
B . y≤-1
C . y≤-1或y>0
D . y<-1或y≥0
如图,在△ABC中,  ,动点P在射线EF上,BP交CE于点D , ∠CBP的平分线交CE于点Q , 当CQ=
,动点P在射线EF上,BP交CE于点D , ∠CBP的平分线交CE于点Q , 当CQ=  CE时,EP+BP=20,则BC的长为.
CE时,EP+BP=20,则BC的长为.
 ,动点P在射线EF上,BP交CE于点D , ∠CBP的平分线交CE于点Q , 当CQ=
,动点P在射线EF上,BP交CE于点D , ∠CBP的平分线交CE于点Q , 当CQ=  CE时,EP+BP=20,则BC的长为.
CE时,EP+BP=20,则BC的长为. 
如图为反比例函数y= 的图象,则k等于( )
的图象,则k等于( )
A . 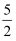 B .
B . 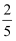 C . 10
D . -10
C . 10
D . -10
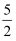 B .
B . 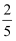 C . 10
D . -10
C . 10
D . -10
反比例函数  在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数
在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数  的图象于点M , △AOM的面积为3.
的图象于点M , △AOM的面积为3.

-
(1) 求反比例函数的解析式;
-
(2)
设点B的坐标为(t , 0),其中t>1.若以AB为一边的正方形有一个顶点在反比例函数
 的图象上,求t的值.
的图象上,求t的值.
若 ,则锐角
,则锐角 等于( )
等于( )
 ,则锐角
,则锐角 等于( )
等于( )
A . 15°
B . 30°
C . 45°
D . 60°
如图,△ABC.的三个顶点分别为A(1,2),B(5,2),C(5,5).若反比例函数  在第一象限内的图象与△ABC有交点,则k的取值范围是( )
在第一象限内的图象与△ABC有交点,则k的取值范围是( )
 在第一象限内的图象与△ABC有交点,则k的取值范围是( )
在第一象限内的图象与△ABC有交点,则k的取值范围是( )
A . 2≤k≤25
B . 2≤k≤10
C . 1≤k≤5
D . 10≤k≤25
最近更新
- Giving small children some money as a gift during the Spring
- (8分) 一元二次方程的二根()是抛物线与轴的两个交点的横坐标,且此抛物线过点.【小题1】(1)求此二次函数的解析式.【
- 已知下列四个命题:①铺得很平的一张白纸是一个平面;②一个平面的面积可以等于6 m2;③平面是矩形或平行四边形形状;④两个
- 关于神经递质的叙述,错误的是( ) A.突触前神经元具有合成递质的能力 B.突触前神经元在静息时能释放神经递质 C.
- 2011年3月5日, 温家宝总理在《政府工作报告》中,首次就楼市调控、稳定房价、违法拆迁、公务用车、财政预算、三公消费、
- 玻璃棒是化学实验中常用的仪器,其作用是用于搅拌、过滤或转移液体时引流。下列有关实验过程中,一般不需要使用玻璃棒进行操作的
- Justas the clothes a person wears, the food he eats and the
- Henry can’t attend the party _____ at Tom’s house at present
- 下图表示不同的生物或成分,下列说法错误的是A.若M表示基因多样性,a~d表示四种不同的植物,则在剧烈变化的环境中最不容易
- 在△ABC中,、为直角边,为斜边,若=7,=5,则△ABC的面积是:
- 鉴别空气,氮气和氧气三种气体,最简单的方法是()A. 分别观察气体的颜色 B. 分别测量气体的密度 C. 分别伸入燃着的
- 二次函数的图象如图所示,则下列结论正确的是A.B.C.D.
- 用氮化硅(Si3N4)陶瓷代替金属制造发动机的耐热部件,能大幅度提高发动机的热效率。工业上用化学气相沉积法制备氮化硅的反
- 20世纪30年代,美国修建田纳西水利工程,苏联修建第聂伯河水电站,两大水利工程在防洪、航运、发电等方面都发挥了巨大的作用
- 依次填入文中横线上的词语,全都恰当的一项是()我们印象最________的是,恒星即使在两个旋臂之间,也像流水一样漂浮在
- One of the greatest benefits of Internet friendships is tha
- 下图描述了一种鹿的种群增长速度的变化,在1935年大约有多少只鹿在特定的环境中生存下去而不会饿死A. 12000
- 甲酸和乙酸都是弱酸,当它们的浓度为0.10mol/L时,甲酸中的约为乙酸中的3倍。现有两种浓度不等的甲酸溶液和,以及0.
- 用斐林试剂鉴定还原糖时,溶液的颜色变化过程是() A.浅蓝色→棕色→砖红色 B.无色→浅蓝色→砖红色 C
- 读明代内阁大学士籍贯分布表,该表所能反映的实质问题是( )南方 北方 南京 浙江 福建 四川 广西 江西 湖广 广



