九年级(初三)数学下学期下册试题
如图,已知△ABC,P是边AB上的一点,连结CP,以下条件中不能确定△ACP与△ABC相似的是( )
A . ∠ACP=∠B
B . ∠APC='∠ACB'
C . AC2=AP·AB
D . 

如图①是由大小相同的小正方体搭成的几何体,将上层的小正方体平移后得到图②.关于平移前后几何体的从三个方向看得图形,下列说法正确的是( )

A . 从正面看到的图相同
B . 从左面看到的图相同
C . 从上面看到的图相同
D . 从三个方向看到的图都不相同
如图所示的紫砂壶,其俯视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图.
①写出△ABC的各点坐标;
②以直角坐标系的原点O为位似中心作△ABC的位似图形△A′B′C′,使△ABC与△A′B′C′的位似比为1:2.

某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“祝”字所在面相对的面上的汉字是( )

A . 考
B . 试
C . 顺
D . 利
网上一家电子产品店,今年1﹣4月的电子产品销售总额如图1,其中一款平板电脑的销售额占当月电子产品销售总额的百分比如图2

根据图中信息,有以下四个结论,推断不合理的是( )
A . 从1月到4月,电子产品销售总额为290万元
B . 平板电脑2﹣4月的销售额占当月电子产品销售总额的百分比与1月份相比都下降了
C . 平板电脑4月份的销售额比3月份有所下降
D . 今年1﹣4月中,平板电脑售额最低的是3月
下面四个几何体中,俯视图是圆的几何体共有( )

A . 1个
B . 2个
C . 3个
D . 4个
如图,在一笔直的海岸线  上有
上有  、
、  两个观测站,
两个观测站,  在
在  的正东方向,
的正东方向,  (单位:
(单位: 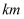 )有一艘小船在点
)有一艘小船在点  处,从
处,从  测得小船在北偏西
测得小船在北偏西  的方向,从
的方向,从  测得小船在北偏东
测得小船在北偏东  的方向.(结果保留根号)
的方向.(结果保留根号)
 上有
上有  、
、  两个观测站,
两个观测站,  在
在  的正东方向,
的正东方向,  (单位:
(单位: 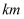 )有一艘小船在点
)有一艘小船在点  处,从
处,从  测得小船在北偏西
测得小船在北偏西  的方向,从
的方向,从  测得小船在北偏东
测得小船在北偏东  的方向.(结果保留根号)
的方向.(结果保留根号)
-
(1) 求点
 到海岸线
到海岸线  的距离;
的距离;
-
(2) 小船从点
 处沿射线
处沿射线  的方向航行一段时间后,到达点
的方向航行一段时间后,到达点  处,此时,从
处,此时,从  测得小船在北偏西
测得小船在北偏西  的方向,求点
的方向,求点  与点
与点  之间的距离.
之间的距离.
已知△ABC∽△DEF,其中AB=5,BC=6,CA=9,DE=3,那么△DEF的周长是 .
如图,一次函数  与反比例函数
与反比例函数  的图象在第一象限交于A,B两点,A点的坐标为
的图象在第一象限交于A,B两点,A点的坐标为  ,B点的坐标为
,B点的坐标为  ,连接
,连接  ,过B作
,过B作  轴,垂足为C.
轴,垂足为C.
 与反比例函数
与反比例函数  的图象在第一象限交于A,B两点,A点的坐标为
的图象在第一象限交于A,B两点,A点的坐标为  ,B点的坐标为
,B点的坐标为  ,连接
,连接  ,过B作
,过B作  轴,垂足为C.
轴,垂足为C. 
-
(1) 求一次函数和反比例函数的表达式;
-
(2) 在射线
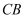 上是否存在一点D,使得
上是否存在一点D,使得  是直角三角形,求出所有可能的D点坐标.
是直角三角形,求出所有可能的D点坐标.
由两块大小不同的正方体搭成如图所示的几何体,它的主视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D .
A,B两地被大山阻隔,若要从A地到B地,只能沿着如图所示的公路先从A地到C地,再由C地到B地.现计划开凿隧道A,B两地直线贯通,经测量得:∠CAB=30°,∠CBA=45°,AC=20km,求隧道开通后与隧道开通前相比,从A地到B地的路程将缩短多少?(结果精确到0.1km,参考数据:  ≈1.414,
≈1.414,  ≈1.732)
≈1.732)
 ≈1.414,
≈1.414,  ≈1.732)
≈1.732)
如图,旗杆及升旗台的剖面和教学楼的剖面在同一平面上,旗杆与地面垂直,在教学楼底部E点处测得旗杆顶端的仰角∠AED=58°,升旗台底部到教学楼底部的距离DE=7米,升旗台坡面CD的坡度i=1:0.75,坡长CD=2米,若旗杆底部到坡面CD的水平距离BC=1米,则旗杆AB的高度约为(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.6)( )

A . 12.6米
B . 13.1米
C . 14.7米
D . 16.3米
“C919”大型客机首飞成功,激发了同学们对航空科技的兴趣,如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸,图中AB∥CD,AM∥BN∥ED,AE⊥DE,请根据图中数据,求出线段BE和CD的长.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,结果保留小数点后一位)

学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为  的小明
的小明  的影子
的影子  长是
长是  ,而小颖
,而小颖  刚好在路灯灯泡的正下方
刚好在路灯灯泡的正下方  点,并测得
点,并测得  .
.
 的小明
的小明  的影子
的影子  长是
长是  ,而小颖
,而小颖  刚好在路灯灯泡的正下方
刚好在路灯灯泡的正下方  点,并测得
点,并测得  .
.

-
(1) 请在图中画出形成影子的光线,并确定路灯灯泡所在的位置
 ;
;
-
(2) 求路灯灯泡的垂直高度
 ;
;
-
(3) 如果小明沿线段BH向小颖(点H)走去,当小明走到BH中点B1处时,请在图中画出此时小明的影长B1C1 , 并求B1C1的长;
如图所示,在  中,斜边
中,斜边 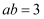 ,
, 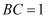 ,点D在AB上,且
,点D在AB上,且  ,则
,则  的值是( )
的值是( )
 中,斜边
中,斜边 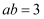 ,
, 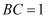 ,点D在AB上,且
,点D在AB上,且  ,则
,则  的值是( )
的值是( ) 
A .  B . 1
C .
B . 1
C .  D .
D . 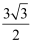
 B . 1
C .
B . 1
C .  D .
D . 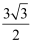
如图,在  中,
中,  ,AD:
,AD: 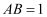 :3,
:3,  ,则DE的长是( )
,则DE的长是( )
 中,
中,  ,AD:
,AD: 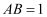 :3,
:3,  ,则DE的长是( )
,则DE的长是( ) 
A . 3
B . 4
C . 5
D . 6
已知α是锐角,sin(α+15°)=  ,则cosα=.
,则cosα=.
 ,则cosα=.
,则cosα=.
如图,在平面直角坐标系中,△ABC为等腰直角三角形,∠ABC=90°,AC∥x轴,经过点B的反比例函数y=  (k>0)交AC于点D,过点D作DE⊥x轴于点E,若AD=3CD,DE=6,则k=
(k>0)交AC于点D,过点D作DE⊥x轴于点E,若AD=3CD,DE=6,则k=
 (k>0)交AC于点D,过点D作DE⊥x轴于点E,若AD=3CD,DE=6,则k=
(k>0)交AC于点D,过点D作DE⊥x轴于点E,若AD=3CD,DE=6,则k= 
已知反比例函数y= 的图象经过点(1,2),则函数y=-kx可为( )
的图象经过点(1,2),则函数y=-kx可为( )
 的图象经过点(1,2),则函数y=-kx可为( )
的图象经过点(1,2),则函数y=-kx可为( )
A . y=-2x
B . y= x
C . y=-
x
C . y=- x
D . y=2x
x
D . y=2x
 x
C . y=-
x
C . y=- x
D . y=2x
x
D . y=2x
最近更新
- 下列图中人物的服饰,能够体现西装传入的是A B C
- 新一轮国务院机构改革方案把政府的行政职能,市场配置资源的基础作用,以及人民群众参与社会事务管理的能力作为一个整体来考虑,
- 下列各组词语中加点词的读音正确的一组是 A.夙兴夜寐(sù) 怪癖(pì
- 某企业要从其下属6个工厂中抽调8名工程技术人员组成课题攻关小组,每厂至少调1人,则这8个名额的分配方案共有( )A
- 某溶液中加入铝粉能产生氢气,在该溶液中一定能大量共存的离子组是() A.Na+、K+、Cl-、SO
- 除去下列物质中的少量杂质,所选试剂或操作方法不正确的一组是( ) 物质 所含杂质 除去杂质的试剂或方法 A NaOH
- 刘禹锡《酬乐天扬州初逢席上见赠》中蕴含人生哲理,给人以鼓舞的两句诗是:________,______________。
- 下列物质中,属于氧化物的是( ) A. SO2 B. Fe(OH)3 C. KClO3
- 2007年,我国全年外商直接投资实际使用金额747.7亿美元,对外投资额187亿美元。这表明,我国在对外开放中 A.
- 由方程确定的函数在上是( ) A.奇函数 B.偶函数 C.增函数
- 黄曲霉素(化学式为C17H12O6)广泛存在于变质的花生、玉米和谷物等农产品中,下列有关说法错误的是( ) A.黄
- 阅读下面的文言文,完成文后小题。 于敏中,字叔子,江苏金坛人。乾隆三年一甲一名进士,授翰林院修撰。以文翰受高宗知,直懋勤
- 下图为某区域经纬网示意图,图中虚线表示某日的昏线位置。读后回答图中所示时刻,甲地的昼长为A.9小时
- 某研究性学习小组以樱桃番茄为材料进行果酒、果醋发酵实验。下列相关叙述正确的是() A.酵母菌是嗜温菌,所以果酒发酵所需的
- 长江在我国众多的河流中居首位的是( ) ①流域面积 ②流程长度 ③含沙量 ④年径流量 ⑤结冰期 ⑥水能蕴藏
- 下列说法正确的是( ) ①1 molO2的质量是32 g·mol—1;②H2的摩尔质量是2 g;③1 molH+的
- 如图所示的电路,电源电压不变,开关S闭合后,当S1由断开变为闭合时,则() A.A1示数变大,A2示数不变 B.A1示
- 培养硝化细菌的碳源、氮源、能源依次是( ) A. 葡萄糖、氨、葡萄糖 B. 葡萄糖、铵盐、太阳能 C.
- 关于“比较过氧化氢在不同条件下的分解”实验,开始实验时4支试管(l号试管对照;2号试管加热;3号试管滴入FeC13溶液;
- 如图甲,在不计滑轮摩擦和绳子质量的条件下,当小车匀速向右运动时,物体A的受力情况是( )A.绳的拉力大于A的重



