九年级(初三)数学下学期下册试题
若反比例函数的图象过点(3,﹣2),则其函数表达式为.
如图,F在BD上,BC、AD相交于点E,且AB∥CD∥EF,
(1)图中有哪几对位似三角形,选其中一对加以证明;
(2)若AB=2,CD=3,求EF的长.

如图,一次函数  与反比例函数的图象交于点
与反比例函数的图象交于点  和点B,与x轴交于点C,与y轴交于点
和点B,与x轴交于点C,与y轴交于点  过点A作
过点A作  轴,垂足为点E,过点B作
轴,垂足为点E,过点B作  轴,垂足为点F,且
轴,垂足为点F,且  ,
,
 与反比例函数的图象交于点
与反比例函数的图象交于点  和点B,与x轴交于点C,与y轴交于点
和点B,与x轴交于点C,与y轴交于点  过点A作
过点A作  轴,垂足为点E,过点B作
轴,垂足为点E,过点B作  轴,垂足为点F,且
轴,垂足为点F,且  ,
, 
-
(1) 求反比例函数的解析式;
-
(2) 求四边形AEFB的面积.
如图,CD=4,∠C=90°,点B在线段CD上,  ,沿AB所在的直线折叠△ACB得到△AC′B,若△DC′B是以BC'为腰的等腰三角形,则线段CB的长为.
,沿AB所在的直线折叠△ACB得到△AC′B,若△DC′B是以BC'为腰的等腰三角形,则线段CB的长为.
 ,沿AB所在的直线折叠△ACB得到△AC′B,若△DC′B是以BC'为腰的等腰三角形,则线段CB的长为.
,沿AB所在的直线折叠△ACB得到△AC′B,若△DC′B是以BC'为腰的等腰三角形,则线段CB的长为. 
如图,⊙O经过等边△ABC的顶点A,C(圆心O在△ABC内),分别与AB,CB的延长线交于点D,E,连结DE,BF⊥EC交AE于点F.

-
(1) 求证:BD=BE;
-
(2) 当AF:EF=4:3,AC=8时,求AE的长.
-
(3) 设
 =m,tan∠DAE=n.求n关于m的函数表达式.
=m,tan∠DAE=n.求n关于m的函数表达式.
如图,正比例函数y=mx与反比例函数y= (m、n是非零常数)的图象交于A、B两点.若点A的坐标为(1,2),则点B的坐标是( )
(m、n是非零常数)的图象交于A、B两点.若点A的坐标为(1,2),则点B的坐标是( )

A . (﹣2,﹣4)
B . (﹣2,﹣1)
C . (﹣1,﹣2)
D . (﹣4,﹣2)
-
(1) 先化简,再求值:(2﹣
 )÷
)÷  ,其中x=2.
,其中x=2.
-
(2) 计算:|
 ﹣2|+2010°﹣(﹣
﹣2|+2010°﹣(﹣  )﹣1+3tan30°.
)﹣1+3tan30°.
现有一张Rt△ABC纸片,直角边BC长为l2cm,另一直角边AB长为24cm.现沿BC边依次从下往上裁剪宽度均为3cm的矩形纸条,如图.已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
A . 第4张
B . 第5张
C . 第6张
D . 第7张
定义:如果一个三角形中有两个内角  满足
满足  ,那我们称这个三角形为“近直角三角形”.
,那我们称这个三角形为“近直角三角形”.
 满足
满足  ,那我们称这个三角形为“近直角三角形”.
,那我们称这个三角形为“近直角三角形”.

-
(1) 若∆ABC是“近直角三角形”,∠B>90°,∠C=50°,则∠A=度;
-
(2) 如图1,Rt∆ABC中,∠BAC=90°,AB=3,AC=4.若BD是∠ABC的平分线,
①求证:∆BDC是“近直角三角形”;
②在边AC上是否存在点E(异于点D),使得∆BCE也是“近直角三角形”?若存在,请求出CE的长;若不存在,请说明理由.
-
(3) 如图2,在Rt∆ABC中,∠BAC=90°,点D为AC边上一点,以BD为直径的圆交BC于点E,连结AE交BD于点F,若∆BCD为“近直角三角形”,且AB=5,AF=3,求tan∠C的值.
如图,小莉用灯泡  照射一个矩形硬纸片
照射一个矩形硬纸片  ,在墙上形成矩形影子
,在墙上形成矩形影子 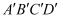 ,现测得
,现测得  ,
,  ,纸片
,纸片  的面积为
的面积为  ,则影子
,则影子 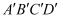 的面积为
的面积为 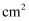 .
.
 照射一个矩形硬纸片
照射一个矩形硬纸片  ,在墙上形成矩形影子
,在墙上形成矩形影子 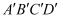 ,现测得
,现测得  ,
,  ,纸片
,纸片  的面积为
的面积为  ,则影子
,则影子 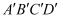 的面积为
的面积为 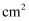 .
. 
如图,∠1=∠2,DE∥AC,则图中的相似三角形有( )

A . 2对
B . 3对
C . 4对
D . 5对
在△ABC中,D为AC上一点,且AC=kAD,E是BC上一点,BD于AE相交于点O,若∠AOB+∠BAC=180°.

-
(1) 如图1,若∠BAC=120°,AB=AC.
①找出与∠ABD相等的角,并证明;
②求
 的值.
的值. -
(2) 如图2,若BE=2CE,求
 的值.
的值.
某大桥采用H型塔型斜拉桥结构(如甲图),图乙是从图甲抽象出的平面图.测得拉索 与水平桥面的夹角是
与水平桥面的夹角是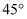 , 拉索
, 拉索 与水平桥面的夹角是
与水平桥面的夹角是 , 两拉索顶端的距离
, 两拉索顶端的距离 为2米,两拉索底端距离
为2米,两拉索底端距离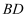 为10米,请求出立柱
为10米,请求出立柱 的长(结果精确到1米).
的长(结果精确到1米).
 与水平桥面的夹角是
与水平桥面的夹角是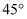 , 拉索
, 拉索 与水平桥面的夹角是
与水平桥面的夹角是 , 两拉索顶端的距离
, 两拉索顶端的距离 为2米,两拉索底端距离
为2米,两拉索底端距离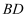 为10米,请求出立柱
为10米,请求出立柱 的长(结果精确到1米).
的长(结果精确到1米).(参考数据: ,
,  ,
,  )
)

如图,菱形ABCD的顶点A在x轴的正半轴上,边CD所在直线过点O,对角线BD∥x轴交AC于点M,双曲线y=  过点B且与AC交于点N,如果AN=3CN,S△NBC=
过点B且与AC交于点N,如果AN=3CN,S△NBC=  ,那么k的值为( )
,那么k的值为( )
 过点B且与AC交于点N,如果AN=3CN,S△NBC=
过点B且与AC交于点N,如果AN=3CN,S△NBC=  ,那么k的值为( )
,那么k的值为( ) 
A . 8
B . 9
C . 10
D . 12
复印纸型号多样,而各型号复印纸之间存在这样的关系:将其中一型号纸张(如A3纸)沿较长边中点的连线对折,就能得到下一型号(A4纸)的纸张,且对折得到的两个矩形和原来的矩形相似(即A3纸与A4纸相似),则这些型号的复印纸宽与长之比为.

如图①,AB=5,射线AM∥BN,点C在射线BN上,将△ABC沿AC所在直线翻折,点B的对应点D落在射线BN上,点P,Q分别在射线AM、BN上,PQ∥AB.设AP=x,QD=y.若y关于x的函数图象(如图②)经过点E(9,2),则cosB的值等于( )

A .  B .
B .  C .
C .  D .
D . 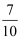
 B .
B .  C .
C .  D .
D . 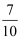
在平面直角坐标系内  点的坐标(
点的坐标(  ,
,  ),则
),则  点关于
点关于  轴对称点
轴对称点  的坐标为( )
的坐标为( )
 点的坐标(
点的坐标(  ,
,  ),则
),则  点关于
点关于  轴对称点
轴对称点  的坐标为( )
的坐标为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,  与反比例函数
与反比例函数  交于点C,D,且
交于点C,D,且  轴,
轴,  的面积为6,若AC:CB=1:3,则反比例函数的表达式为.
的面积为6,若AC:CB=1:3,则反比例函数的表达式为.
 与反比例函数
与反比例函数  交于点C,D,且
交于点C,D,且  轴,
轴,  的面积为6,若AC:CB=1:3,则反比例函数的表达式为.
的面积为6,若AC:CB=1:3,则反比例函数的表达式为.

在△ABC中,∠A,∠C都是锐角,cosA= , sinC=
, sinC= , 则∠B=.
, 则∠B=.
 , sinC=
, sinC= , 则∠B=.
, 则∠B=.
已知点A(2,  )、B(3,
)、B(3, 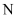 )在函数
)在函数  的图象上,则
的图象上,则  、
、  的大小关系是:
的大小关系是: 
 .(用>,<,=填空).
.(用>,<,=填空).
 )、B(3,
)、B(3, 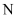 )在函数
)在函数  的图象上,则
的图象上,则  、
、  的大小关系是:
的大小关系是: 
 .(用>,<,=填空).
.(用>,<,=填空).
最近更新
- 根据下面的材料,概括我国使用普通话情况的两个特点。 国家语委近日开展的一项调查显示,民众中没上过小学的有0.36%的人会
- 下列有关环境问题都是由化学物质引起的,在下列组合中对应的化合物不正确的是 A.白色污染:废弃塑料
- 用两根绳子吊起一个重物,如图10所示,如果每根绳所能承受的最大拉力是2.0104N(sin37º=0.6,sin53º=
- 到目前为止,由化学能转变的热能或电能仍然是人类使用的最主要的能源. (1)在25℃、101kPa下,16g的甲醇(CH3
- 假定某国全年全社会商品零售价格总额为30000亿元,货币流通速度为6次,通货膨胀率为5%,当年该国发行的纸币是
- 2005年全国高考于6月7日上午9时正式开始,理科综合考试从8日下午3时开始,考试时间为2.5小时,试判断哪些是时间,哪
- 如图,等腰梯形ABCD中,AD∥BC,点E,F在BC上,且BE=FC,连接DE,AF.求证:DE=AF.
- Have you ever fancied sailingaround the world or buying a ho
- In China, all the students work hard at school _________ goi
- 南京临时政府颁布《临时约法》的目的之一是限制袁世凯的权力,体现这一目的的主要规定是 A. 主权属于国民全体 B.各民
- 下列加点字注音完全正确的一项是( )A. 藩篱( fān) 镂空(lóu) 鸣钟击
- 实验室所用的某种过氧化氢溶液中,水与过氧化氢的质量比为9:1,则该溶液中氢、氧元素的原子个数比是 A.17:1
- 下列各句中横线上填入的词语正确的一组是()①各级政府要切实解决侵害妇女儿童权益和___________妇女儿童发展的突出
- 下列变化不属于缓慢氧化的是( ) A.动植物呼吸 B.酒的酿造 C.氢气的燃烧 D.农家肥的腐熟
- (03年上海卷)某登山爱好者在攀登珠穆朗玛峰的过程中,发现他携带的手表表面玻璃发生了爆裂。这种手表是密封的,出厂时给出的
- (07全国卷二)根据相关资料回成下列问题。考古材料证明,玉米最早是在美洲培育出的。哥伦布将这种“奇异的谷物”带回欧洲后,
- 图1是某生物的一个初级精母细胞,图2是该生物的五个精细胞。根据图中的染色体类型和数目,判断最可能来自同一个次级精母细胞的
- 四棱锥中,平面,,底面为直角梯形分别是的中点(Ⅰ)求证:// 平面; (Ⅱ)求截面与底面所成二面角的大小; (Ⅲ)求点到
- 从哲学角度分析,“神舟”一号到六号飞船发射成功说明了①认识和实践的辩证统一关系 ②只要发挥主观能动性,就能认识和利用规律
- 阅读下面的文字,完成下列小题。归去来兮,田园将芜胡不归?既自以心为形役,奚惆怅而独悲?悟已往之不谏,知来者之可追。实迷途



