九年级(初三)数学下学期下册试题
正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫格点三角形.在图中正方形网格(每个小正方形边长为1)中有一格点△ABC和一线段DE
(1)以DE为一边做格点△DEF与△ABC相似;
(2)直接写出△DEF的面积.

如图,在常见的几何体圆锥、圆柱、球、长方体中,主视图与它的左视图一定完全相同的几何体有.(填编号)

如图,一辆轿车在一个十字路口遇到红灯刹车停下,轿车里的驾驶员看地面的斑马线前后两端的视角分别是  和
和  ,如果斑马线的宽度
,如果斑马线的宽度 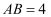 米,驾驶员与车头的距离是1.8米,这时轿车车头与斑马线的距离
米,驾驶员与车头的距离是1.8米,这时轿车车头与斑马线的距离  约是多少米?(参考数据:
约是多少米?(参考数据:  ,
,  ,
,  ,
, 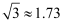 ,结果精确到0.1米)
,结果精确到0.1米)
 和
和  ,如果斑马线的宽度
,如果斑马线的宽度 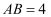 米,驾驶员与车头的距离是1.8米,这时轿车车头与斑马线的距离
米,驾驶员与车头的距离是1.8米,这时轿车车头与斑马线的距离  约是多少米?(参考数据:
约是多少米?(参考数据:  ,
,  ,
,  ,
, 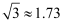 ,结果精确到0.1米)
,结果精确到0.1米) 
如图,已知O是坐标原点,B,C两点的坐标分别为(3,-1),(2,1).

-
(1) 以O点为位似中心,在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形;
-
(2) 如果△OBC内部一点M的坐标为(x,y),写出B,C,M的对应点B′,C′,M′的坐标.
如图,在  中,
中,  ,点
,点  在
在  边上,
边上,  ,点
,点  在AC上,
在AC上,  ,垂足为
,垂足为  ,若
,若  ,
,  ,则线段
,则线段  的长为.
的长为.
 中,
中,  ,点
,点  在
在  边上,
边上,  ,点
,点  在AC上,
在AC上,  ,垂足为
,垂足为  ,若
,若  ,
,  ,则线段
,则线段  的长为.
的长为. 
已知一个圆锥的底面半径为3cm,母线长为10cm,则这个圆锥的侧面积为( )
A . 15πcm2
B . 30πcm2
C . 60πcm2
D . 3 cm2
cm2
 cm2
cm2
如图,在△ABC中,D、E为边AB、AC的中点,已知△ADE的面积为4,那么△ABC的面积是.

如图1所示,在等边三角形ABC中,线段AD为其内角平分线,过点D的直线B1C1⊥AC于点C1 , 交AB的延长线于点B1 .

-
(1) 请你探究:
 是否都成立?请说明理由.
是否都成立?请说明理由.
-
(2) 请你继续探究:若
 ABC为任意三角形,线段AD为其内角平分线,
ABC为任意三角形,线段AD为其内角平分线,  一定成立吗?并证明你的判断.
一定成立吗?并证明你的判断.
-
(3) 如图2所示,在Rt
 ABC中,∠ACB=90°,AC=8,AB=
ABC中,∠ACB=90°,AC=8,AB=  ,E为AB上一点且AE=5,CE交内角平分线AD于点F,试求
,E为AB上一点且AE=5,CE交内角平分线AD于点F,试求  的值.
的值.
一个圆柱的轴截面平行于投影面,圆柱的正投影是邻边长分别为4cm,3cm的矩形,求圆柱的表面积和体积.
如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,BC=  ,AC=3,则sin∠ACD=( )
,AC=3,则sin∠ACD=( )
 ,AC=3,则sin∠ACD=( )
,AC=3,则sin∠ACD=( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.

-
(1) 求证:△ADE∽△ABC;
-
(2) 若AD=3,AB=5,求
 的值.
的值.
如图,已知 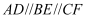 ,那么下列结论正确的是( )
,那么下列结论正确的是( )
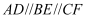 ,那么下列结论正确的是( )
,那么下列结论正确的是( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,从观察点A处发现北偏东45°方向,距离为9海里的B处有一走私船。这时一艘缉私艇位于A点的北偏西53°方向的C处,且C点恰好在B点的正西方向。此时走私船正以每小时50海里的速度从B处向北偏东30°方向逃窜,缉私艇奉命立即以每小时50 海里的速度向走私船追去。

-
(1) 点B和点C相距多少海里?
-
(2) 缉私艇沿什么方向行驶,才能在最短时间内追上走私船?并求出所需时间.(参考数据:sin53º≈0.8,cos53º≈0.6,
 )
)
45°的正弦值为( )
A . 1
B .  C .
C .  D .
D . 
 C .
C .  D .
D . 
已知二次函数  .
.
 .
. 
-
(1) 当该二次函数的图象经过点
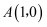 时,求该二次函数的表达式;
时,求该二次函数的表达式;
-
(2) 在(1) 的条件下,二次函数图象与x轴的另一个交点为点B , 与y轴的交点为点C , 点P从点A出发在线段AB上以每秒2个单位长度的速度向点B运动,同时点Q从点B出发,在线段BC上以每秒1个单位长度的速度向点C运动,直到其中一点到达终点时,两点停止运动,求△BPQ面积的最大值;
-
(3) 若对满足
 的任意实数x , 都使得
的任意实数x , 都使得 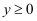 成立,求实数b的取值范围.
成立,求实数b的取值范围.
△OAB是⊙O的内接三角形,∠AOB=120°,过O作OE⊥AB于点E,交⊙O于点C,延长OB至点D,使OB=BD,连CD.

-
(1) 求证: CD是⊙O切线;
-
(2) 若F为OE上一点,BF的延长线交⊙O于G,连OG,
 ,CD=6
,CD=6  ,求S△GOB .
,求S△GOB .
一个物体如图所示,它的俯视图是( )

A .  B .
B .  C .
C .  D .
D . 
 C .
C .  D .
D .
如图是一个正方体纸盒的展开图,如果这个正方体纸盒相对两个面上的代数式相等,求x,y,z的值.

已知反比例函数y= 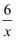 ,当1<x<3时,y的取值范围是( )
,当1<x<3时,y的取值范围是( )
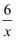 ,当1<x<3时,y的取值范围是( )
,当1<x<3时,y的取值范围是( )
A . 0<y<l
B . 1<y<2
C . y>6
D . 2<y<6
在△ABC中,sinA=  ,AB=8,BC=6,则AC=.
,AB=8,BC=6,则AC=.
 ,AB=8,BC=6,则AC=.
,AB=8,BC=6,则AC=.
最近更新
- 利用研究弹力和弹簧伸长关系的实验,测定弹簧的劲度系数。用一测力计水平拉一端固定的弹簧,测出的几组弹力F与弹簧长度L对应的
- Itwas so dark that the little boy _______. A. didn't dare
- 现有5种短周期元素X、Y、Z、Q、W,原子序数依次增大,在周期表中X原子半径最小;X和W同主族;Y元素原子核外电子总数是
- 在(1+2x)n展开式中含x2的项的系数等于含x的项的系数的8倍,则n等于A.11
- 导致我国南、北方耕作制度产生很大差异的最主要因素是( ) A.地形 B.水源 C.土
- 读图,完成问题。岩石化学风化最强烈的是( ) A.M B
- 经国务院、中央军委批准建设的海南航天发射场,2009年9月14日在海南文昌市动工建设,预计将于2013年完工并投入使用。
- 阅读下列材料: 材料一 仲弓问仁。子曰:“出门如见大宾,使民如承大祭。己所不欲,勿施于人。在邦无怨,在家无怨。”仲弓曰
- 完成或配平下列化学方程式 (1)写出有水生成的化合反应,分解反应,置换反应各一个化学方程式 (2)配平下列化学方程式
- 走进水果批发市场,我们偶尔闻到一阵酒的味道,水果储藏时间久了产生酒味的原因是( ) A.细菌的分解作用
- 一定条件下,将SO2和O2充入一密闭容器中,发生如下反应:2SO2(g)+O2(g) 2SO3(g) ΔH<0,反
- 检疫工作人员发现,一种新型的使鸡、鸭等禽类患病死亡的微生物没有细胞结构,你推测这 种病原体属于( ) A.细菌 B
- 下图是新鲜绿叶的四种光合色素在滤纸上分离的情况,以下说法正确的是
- 日常生活中的下列做法,不能用化学变化做出解释的是() A.食盐做调味品和防腐剂 B.苹果催熟香蕉,柿子等水果 C.汽油洗
- 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点. (Ⅰ)求证:AB1⊥A1D; (Ⅱ)求点C到平面A
- 椭圆的半焦距为,若直线与椭圆的一个交点的横坐标恰为,则椭圆的离心率_________________.
- 如图表示人体内氧元素随化合物代谢转移过程,下列分析合理的是() A. ①过程发生在核糖体中,水中的H只来自于一NH2 B
- 如果f(x)=a且f(x)=a,那么就说当x趋向于无穷大时,函数f(x)的极限为____________,记作f(x)=
- 这是西周分封略图,西周初年实行分封制是为了:A、巩固对周边的统治 B、镇压奴隶和平民的反抗
- 材料一:马克思主义是发展的理论,它随着社会实践的发展而发展。马克思主义在中国传播和发展的过程就是马克思主义中国化的过程,



