九年级(初三)数学下学期下册试题
已知:如图,在  中,D是AC上一点,E是AB上一点,且∠AED=∠C.
中,D是AC上一点,E是AB上一点,且∠AED=∠C.
 中,D是AC上一点,E是AB上一点,且∠AED=∠C.
中,D是AC上一点,E是AB上一点,且∠AED=∠C.
-
(1) 求证:△AED∽△ACB;
-
(2) 若AB=6,AD=4,AC=5,求AE的长。
由六个相同的立方体拼成的几何体如图所示,则它的主视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,A、B是双曲线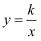
 上的点,A、B两点的横坐标分别是a、3a,线段AB的延长线交x轴于点C,若S△AOC=6,则k的值为( )
上的点,A、B两点的横坐标分别是a、3a,线段AB的延长线交x轴于点C,若S△AOC=6,则k的值为( )
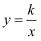
 上的点,A、B两点的横坐标分别是a、3a,线段AB的延长线交x轴于点C,若S△AOC=6,则k的值为( )
上的点,A、B两点的横坐标分别是a、3a,线段AB的延长线交x轴于点C,若S△AOC=6,则k的值为( )
A . 2
B . 3
C . 4
D . 6
在△ABC中,  ,则△ABC为( )
,则△ABC为( )
 ,则△ABC为( )
,则△ABC为( )
A . 直角三角形
B . 等边三角形
C . 含60°的任意三角形
D . 是顶角为钝角的等腰三角形
已知如图,在  中,点
中,点  、点
、点  分别在
分别在  、
、  边上,且
边上,且  ,
,  ,
,  ,
,  的面积为4,则
的面积为4,则  的面积为( )
的面积为( )
 中,点
中,点  、点
、点  分别在
分别在  、
、  边上,且
边上,且  ,
,  ,
,  ,
,  的面积为4,则
的面积为4,则  的面积为( )
的面积为( ) 
A . 5
B . 6
C . 8
D . 9
已知如图为一几何体的三视图.

(1)写出这个几何体的名称.
(2)在虚线框中画出它的一种表面展开图.
(3)若主视图中长方形的长为8cm,俯视图中三角形的边长为3cm,求这个几何体的侧面积.
如图,点O为直线AB外一定点,点P线段AB上一动点,在直线OP右侧作Rt△OPQ,使得∠OPQ=  ,已知AB=3,当点P从点A运动到点B时,点Q运动的路径长是.
,已知AB=3,当点P从点A运动到点B时,点Q运动的路径长是.
 ,已知AB=3,当点P从点A运动到点B时,点Q运动的路径长是.
,已知AB=3,当点P从点A运动到点B时,点Q运动的路径长是. 
在正方形ABCD中,对角线AC,BD交于点O,点P在线段BC上(不含点B),∠BPE=  ∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
 ∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
-
(1) 当点P与点C重合时(如图1).求证:△BOG≌△POE;
-
(2) 通过观察、测量、猜想:求
 的值,并结合图2证明你的猜想;
的值,并结合图2证明你的猜想;
-
(3) 把正方形ABCD改为菱形,其他条件不变(如图3),若∠ACB=α,求
 的值.(用含α的式子表示)
的值.(用含α的式子表示)
BD为等腰△ABC的腰AC上的高,BD=1,tan∠ABD=  ,则CD的长为.
,则CD的长为.
 ,则CD的长为.
,则CD的长为.
下列函数中,图象经过原点的是( )
A .  B .
B .  C .
C . 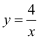 D .
D . 
 B .
B .  C .
C . 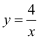 D .
D . 
如图是一个用硬纸板制作的长方体包装盒展开图,已知它的底面形状是正方形,高为12cm.

-
(1) 制作这样的包装盒需要多少平方厘米的硬纸板?
-
(2) 若1平方米硬纸板价格为5元,则制作10个这的包装盒需花费多少钱?(不考虑边角损耗)
下列说法:①所有等腰三角形都相似;②有一个底角相等的两个等腰三角形相似;③有一个角相等的等腰三角形相似;④有一个角为60°的两个直角三角形相似,其中正确的说法是( ).
A . ②④
B . ①③
C . ①②④
D . ②③④
若反比例函数y=(m+1) 的图象在第二、四象限,m的值为
的图象在第二、四象限,m的值为
 的图象在第二、四象限,m的值为
的图象在第二、四象限,m的值为
如图,已知∠1=∠2,那么添加一个条件后,仍不能判定△ABC与△ADE相似的是( )

A . ∠C=∠AED
B . ∠B=∠D
C .  D .
D . 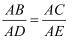
 D .
D . 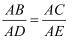
已知A(x1 , y1),B(x2 , y2)是反比例函数y=﹣  图象上的两点,且x1>x2>0,则y1y2(填“>”或“<”).
图象上的两点,且x1>x2>0,则y1y2(填“>”或“<”).
 图象上的两点,且x1>x2>0,则y1y2(填“>”或“<”).
图象上的两点,且x1>x2>0,则y1y2(填“>”或“<”).
如图,A、B两个码头分别在一条河的两岸AC、BD上,河岸AC、BD均为东西走向,一艘客轮以每小时30千米的速度由A码头出发沿北偏东50°的方向航行至B码头,用时1.2小时,求该河的宽度(结果精确到1千米)
【参考数据:sin50°=0.77,cos50°=0.64,tan50°=1.20】

如图

-
(1) 如图1所示,在Rt△ABC中,∠ACB=90°,AC=BC,点D在斜边AB上,点E在直角边BC上,若∠CDE=45°,求证:△ACD∽△BDE.
-
(2) 如图2所示,在矩形ABCD中,AB=4cm,BC=10cm,点E在BC上,连接AE,过点E作EF⊥AE交CD(或CD的延长线)于点F.
①若BE:EC=1:9,求CF的长;
②若点F恰好与点D重合,请在备用图上画出图形,并求BE的长.
如图,过反比例函数  (
(  )的图象上一点
)的图象上一点  作
作  轴于点B,连接
轴于点B,连接 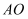 ,若
,若  ,则反比例函数的表达式为.
,则反比例函数的表达式为.
 (
(  )的图象上一点
)的图象上一点  作
作  轴于点B,连接
轴于点B,连接 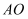 ,若
,若  ,则反比例函数的表达式为.
,则反比例函数的表达式为. 
若点A(x1 , ﹣3)、B(x2 , ﹣2)、C(x3 , 1)在反比例函数  的图象上,则x1、x2、x3的大小关系是( )
的图象上,则x1、x2、x3的大小关系是( )
 的图象上,则x1、x2、x3的大小关系是( )
的图象上,则x1、x2、x3的大小关系是( )
A . x1<x2<x3
B . x3<x1<x2
C . x2<x1<x3
D . x3<x2<x1
将油箱注满k升油后,轿车可行驶的总路程S(单位:千米)与平均耗油量a(单位:升/千米)之间是反比例函数关系  (k是常数,k≠0).已知某轿车油箱注满油后,以平均耗油量为每千米耗油0.1升的速度行驶,可行驶700千米.
(k是常数,k≠0).已知某轿车油箱注满油后,以平均耗油量为每千米耗油0.1升的速度行驶,可行驶700千米.
 (k是常数,k≠0).已知某轿车油箱注满油后,以平均耗油量为每千米耗油0.1升的速度行驶,可行驶700千米.
(k是常数,k≠0).已知某轿车油箱注满油后,以平均耗油量为每千米耗油0.1升的速度行驶,可行驶700千米.
-
(1) 求该轿车可行驶的总路程S与平均耗油量a之间的函数解析式;
-
(2) 当平均耗油量少于0.07升/千米时,该轿车至少可以行驶多少千米?
最近更新
- (本小题满分10分) 中,为边上的一点,,,,求. 【命题意图】本试题主要考查同角三角函数关系、两角和差公式和正弦定理在
- 2009年3月,十一届人大二次会议在人民大会堂举行。据报道,十一届人大二次会议秘书处议案组收到的提案不但议题广泛,而且形
- .“电动葫芦”普遍使用的起重设备(如图),它通过电动机和一个动滑轮将物体提高,如图“电动葫芦”将0.9t的钢材匀速吊起1
- 附加题 一天的工作结束了,加莉亚把记下来的东西念给保尔听,她发现保尔全
- 广东省委省政府2009年4月公布的《关于实施珠三角地区改革发展规划纲要的决定》中有这样三句口号:“先干不评论,先试不议论
- 一位同学实验获得几组数据以后,采用图像分析实验数据。将相应的力F和加速度a,在F—a图中描点并拟合成一条直线,如图所示。
- It seems that living green is ______ easy and affordable. A
- 某有机化合物的结构简式如图所示,下列说法正确的是()A.不能发生银镜发应 B.1mol 该物质最多可与2molBr2反应
- 在横线处写出诗文原句。(限选其中4道题)(8分) ①《曹刿论战》中对战争场面的描写,作者只用了“齐人三鼓”、“ ”和“
- 下列词语中加点汉字的读音,全都不相同的一组是() A.蝉联 禅让 殚精竭虑 箪食壶浆 B.
- 如图在三棱柱ABC-中,已知底面ABC是底角等于,底边AC=的等腰三角形,且,面与面ABC成,与交于点E。1)
- 下列各项中最适合填在横线上的一项是 从这个意义上讲,我们希望孔了是灰色的。或者说,我们愿意把他看作是灰色的。但是,没有
- 已知圆锥的底面直径和母线长都是 (1)求该圆锥的外接球的表面积; (2)正方体的一面在该圆锥的底面上,其余四个顶点在圆锥
- It was a Sundayafternoon and Sophie was searching her toy bo
- (1)已知函数f(x)=lg(x2+2x+a),若其定义域为R,求a的取值范围;(2)已知函数f(x)=lg(x2+2x
- 阅读下面的文字,完成1~3题。 秦朝的“铁路” 近来在河南南阳的山区里发现了古代的“铁路”。经碳14测定,系22
- 一根长0.1m的细线,一端系着一个质量是0.18kg的小球,拉住线的另一端,使球在光滑的水平桌面上做匀速圆周运动,当小球
- People do not analyse every problem they meet. Sometimes the
- 将如图形状的纸片折成一个立方体,数字在与数字2所在平面相对的平面上.
- 下列对有关实验现象的描述错误的是()A. 铁丝在氧气中燃烧时,火星四射,有黑色物质生成 B. 硫在氧气中燃烧,发出明亮的



