九年级(初三)数学下学期下册试题
如图,已知  中,
中,  为边
为边  上一点,
上一点,  为边
为边  上一点,
上一点,  ,
,  ,
, 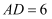 ,当
,当  的长度为______时,
的长度为______时,  和
和  相似.( )
相似.( )
 中,
中,  为边
为边  上一点,
上一点,  为边
为边  上一点,
上一点,  ,
,  ,
, 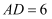 ,当
,当  的长度为______时,
的长度为______时,  和
和  相似.( )
相似.( ) 
A . 9
B . 6
C . 4或9
D . 6或9
小明想用一个圆心角为120°,半径为6cm的扇形做一个圆锥的侧面(接缝处忽略不计),则做成的圆锥底面半径为( )
A . 1 cm
B . 2 cm
C . 3 cm
D . 4cm
有一种落地晾衣架如图1所示,其原理是通过改变两根支撑杆夹角a的度数来调整晾杆的高度,图2是晾衣架的侧面的平面示意图,AB和CD分别是两根长度不等的支撑杆,夹角∠BOD=a,AO=70cm,BO=DO=80cm,CO=40cm。

-
(1) 若a=56°,求点A离地面的高度AE;
(参考值:sin62°=cos28°≈0.88,sin28°=cos62°≈0.47,tan62°≈1.88,tan28°≈0.53)
-
(2) 调节a的大小,使A离地面高度AE=125cm时,求此时C点离地面的高度CF。
已知:如图,△ABC中,AD⊥BC于D,AD=200,∠B=30°,∠C=45°.求BC的长.

如图,某教学兴趣小组想测量某建筑物的高度,他们在A点测得屋顶C的仰角为30°,然后沿AD方向前进10米,到达B点,在B点测得屋顶C的仰角为60°,已知测量仪AE的高度为1米,请你根据他们的测量数据计算建筑物CF的高度(结果保留根号).

图1是某长征主题公园的雕塑,将其抽象成如图2所示的示意图,已知 , A,D,H,G四点在同一直线上,测得
, A,D,H,G四点在同一直线上,测得 . (结果保留小数点后一位)
. (结果保留小数点后一位)
 , A,D,H,G四点在同一直线上,测得
, A,D,H,G四点在同一直线上,测得 . (结果保留小数点后一位)
. (结果保留小数点后一位)
-
(1) 求证:四边形
 为平行四边形;
为平行四边形;
-
(2) 求雕塑的高(即点G到
 的距离).
的距离).(参考数据:
 )
)
如图,在正方形网格中,每个小正方形的边长都是1,  是
是  的外接圆,点A , B , O在网格线的交点上,则
的外接圆,点A , B , O在网格线的交点上,则  的值是.
的值是.
 是
是  的外接圆,点A , B , O在网格线的交点上,则
的外接圆,点A , B , O在网格线的交点上,则  的值是.
的值是. 
如图,电线杆CD的高度为h,两根拉线AC与BC相互垂直,∠CAB=a,则拉线BC的长度为(A,D,B在同一条直线上)( )

A .  B .
B .  C .
C .  D . h·cosa
D . h·cosa
 B .
B .  C .
C .  D . h·cosa
D . h·cosa
下面4个图均由6个小正方形组成,若以每个小正方形为面,则可以折叠成正方体的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 

-
(1) 【问题再现】苏科版《数学》八年级下册第94页有这样一题:
如图1,在正方形ABCD中,E,F,G分别是BC,CD,AD上的点,
 , 垂足为M,那么GEBF(填“<”、“=”或“>”).
, 垂足为M,那么GEBF(填“<”、“=”或“>”). -
(2)
【迁移尝试】如图2,在5×6的正方形网格中,点A,B,C,D为格点,AB交CD于点M.求 的度数;
的度数;
-
(3) 【拓展应用】如图3,点P是线段AB上的动点,分别以AP,BP为边在AB的同侧作正方形APCD与正方形PBEF,连接DE分别交线段BC,PC于点M,N.
①求 的度数;
的度数;
②连接AC交DE于点H,直接写出 的值为______.
的值为______.
如图,在△ABC中,DE//BC,AD∶DB=1∶2, 若DE=3,则BC=.

如图,在正方形ABCD中,E,F分别为BC,CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长于点Q,下列结论正确的有( )个.

①AE⊥BF; ②QB=QF; ③  ; ④SECPG=3S△BGE
; ④SECPG=3S△BGE
A . 1
B . 4
C . 3
D . 2
小李要外出参加“建国70周年”庆祝活动,需网购一个拉杆箱,图①,②分别是她上网时看到的某种型号拉杆箱的实物图与示意图,并获得了如下信息:滑杆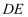 , 箱长
, 箱长 , 拉杆
, 拉杆 的长度都相等,
的长度都相等, 在
在 上,
上, 在
在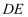 上,支杆
上,支杆
 , 请根据以上信息,解决下列向题.
, 请根据以上信息,解决下列向题.
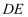 , 箱长
, 箱长 , 拉杆
, 拉杆 的长度都相等,
的长度都相等, 在
在 上,
上, 在
在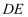 上,支杆
上,支杆
 , 请根据以上信息,解决下列向题.
, 请根据以上信息,解决下列向题.

-
(1) 求
 的长度(结果保留根号);
的长度(结果保留根号);
-
(2) 求拉杆端点
 到水平滑杆
到水平滑杆 的距离(结果保留根号).
的距离(结果保留根号).
现在各地房产开发商,为了获取更大利益,缩短楼间距,以增加住宅楼栋数。合肥市某小区正在兴建的若干幢20层住宅楼,国家规定普通住宅层高宜为2.80米.如果楼间距过小,将影响其他住户的采光(如图所示,窗户高1.3米)。
(1)合肥的太阳高度角(即正午太阳光线与水平面的夹角):夏至日为81.4度,冬至日为34.88度。为了不影响各住户的采光,两栋住宅楼的楼间距至少为多少米?
(2)有关规定:平行布置住宅楼,其建筑间距应不小于南侧建筑高度的1.2倍;按照此规定,是否影响北侧住宅楼住户的全年的采光?若有影响,试求哪些楼层的住户受到影响?
(本题参考值:sin81.4º="0.99," cos81.4º="0.15," tan81.4º="6.61;" sin34.88º="0.57," cos34.88º="0.82," tan34.88º=0.70)
如图,是一个正方体骰子的表面展开图,将其折叠成正方体骰子(点数朝外),如果1点在上面,3点在左面,在前面的点数为( )

A . 2
B . 4
C . 5
D . 6
已知反比例函数y= 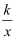 的图象过点A(1,﹣2),则k的值为( )
的图象过点A(1,﹣2),则k的值为( )
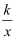 的图象过点A(1,﹣2),则k的值为( )
的图象过点A(1,﹣2),则k的值为( )
A . 1
B . 2
C . ﹣2
D . ﹣1
如图,在△ABC中,AB≠AC.D、E分别为边AB、AC上的点.AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件:,可以使得△FDB与△ADE相似.(只需写出一个)

如图所示几何体的左视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,是一个半径为6cm , 面积为12πcm2的扇形纸片,现需要一个半径为R的圆形纸片,使两张纸片刚好能组合成圆锥体,则R等于cm .

如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(﹣1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.已知点B′的坐标是(3,﹣1),则点B的坐标是.

最近更新
- 设集合,集合,则( ) A.中有3个元素B.中有1个元素C.中有2个元素 D.
- I work as a postal letter carrier in Charlotte. One day seve
- “6”字形图中,FM是大⊙O的直径,BC与大⊙O相切于B, OB与小⊙O相交于点A,AD∥BC,CD∥BH∥FM,
- 端午节吃粽子是中华民族的传统习俗,五月初五早上,奶奶为小明准备了四只粽子:一 只肉馅,一只香肠馅,两只红枣馅,四
- 煤、石油、天然气是重要的化石燃料,下列关于化石燃料的叙述错误的是()A. 石油是一种化工产品 B. 将石油分馏可得到多种
- Ⅰ.2017年08月08日21时19分46秒在四川阿坝州九寨沟县发生7级地震。地震后,为防止疫病流行,全国各地向灾区运
- 发射火箭推进器中盛有液态肼(X)和双氧水(H2O2),当它们混合反应时,放出大量的热量。关反应的化学方程式为:X + 2
- 阅读下列材料,回答问题:(12分) 材料一:(晁错)说上曰:“昔高祖初定天下,昆弟少,诸子弱,大封同姓。……今削之亦反,
- 将一定质量的金属锌投入63.7g稀硫酸中,恰好完全反应,放出气体的质量与反应时间的关系如图所示.试求(计算结果精确到0.
- 雨后的夜晚,当你迎着月光行走在有积水的路上,为了避让水洼,应走“较暗”的地面.这是因为光在()A.地面大发生镜面发射 B
- 如图,其中含有三个正方形,图中有几种全等三角形?请分别写出来.
- 金属是一种重要的材料,人类的生活和生产都离不开金属,全世界每年因生锈损失的钢铁,约占世界年产量的十分之一. (1)兴趣小
- 隋朝末年,家住涿郡的一位商人要沿着新开通的大运河乘船去洛阳,他必须经过 ( ) A.永济渠 B
- 下列说法中,正确的是( )A. 满足不等式的的最大负整数是B. 若点、、在双曲线上,则C. 将双曲线绕原点旋转
- Thenew secretary is a quick, ______ worker, and the boss is
- 右图为咱们百色凌云县茶山“金字塔”景区,一年一度的凌云茶文化 节常常在此举行。高度浓缩了凌云近千年的茶文化,吸引众多中外
- “我带了几双眼下中国还不能生产的尼龙袜子送给父亲,还带了一脑袋关于原子弹的知识献给祖国”,这是邓稼先归国时的一段话,这段
- 根据要求作文。前段时间,舟山连续的阴雨天让我们每一个舟山人又一次真切地感受到了阳光的可贵,是啊!自然万物因为拥有了阳光而
- 甲、乙、丙、丁分别是Ba(NO3)2、NaOH、H2SO4、K2CO3四种无色溶液中的一种,现将其两两混合,现象如下表所
- 同一状态下, 20mL A2气体与30mL B2气体恰好完全反应生成20mL 某气体X, 则X的化学式为 A.A2 B3



