九年级(初三)数学下学期下册试题
如图,P是反比例函数图象上第二象限内一点,若矩形PEOF的面积为3,则反比例函数的解析式是( )

A . y=  B . y=﹣
B . y=﹣ 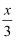 C . y=
C . y= 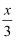 D . y=
D . y= 
 B . y=﹣
B . y=﹣ 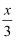 C . y=
C . y= 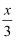 D . y=
D . y= 
如图,在△ABC中,DE∥BC,AB=2BD,则  =.
=.
 =.
=. 
如图所示,反比例函数y=  的图象与一次函数y=kx﹣3的图象在第一象限内相交于点A(4,m).
的图象与一次函数y=kx﹣3的图象在第一象限内相交于点A(4,m).

-
(1) 求m的值及一次函数的解析式;
-
(2) 若直线x=2与反比例和一次函数的图象分别交于点B、C,求线段BC的长.
下图是小红在某天四个时刻看到一根木棒及其影子的情况,那么她看到的先后顺序是 .

如图是正方体的表面展开图,请问展开前与“我”字相对的面上的字是( )

A . 是
B . 好
C . 朋
D . 友
我国古代数学著作《九章算术》中记载了一个问题:“今有邑方不知大小,各开中门,出北门三十步有木,出西门七百五十步见木,问:邑方几何?” .其大意是:如图,一座正方形城池,A为北门中点,从点A往正北方向走30步到B出有一树木,C为西门中点,从点C往正西方向走750步到D处正好看到B处的树木,求正方形城池的边长.

先化简,再求值:  ,其中m=tan60°-
,其中m=tan60°-  .
.
 ,其中m=tan60°-
,其中m=tan60°-  .
.
如图,放映幻灯时,通过光源,把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为cm.

如图所示,在数轴上点A所表示的数x的范围是( )
A .  sin30°<x<sin60°
B . cos30°<x<
sin30°<x<sin60°
B . cos30°<x< cos45°
C .
cos45°
C .  tan30°<x<tan45
D .
tan30°<x<tan45
D .  cot45°<x<cot30°
cot45°<x<cot30°
 sin30°<x<sin60°
B . cos30°<x<
sin30°<x<sin60°
B . cos30°<x< cos45°
C .
cos45°
C .  tan30°<x<tan45
D .
tan30°<x<tan45
D .  cot45°<x<cot30°
cot45°<x<cot30°
如图,在正方形  中,
中,  、
、  分别是边
分别是边  、
、  上的点,
上的点,  ,
,  ,连接
,连接  并延长交
并延长交  的延长线于点
的延长线于点  .
.
 中,
中,  、
、  分别是边
分别是边  、
、  上的点,
上的点,  ,
,  ,连接
,连接  并延长交
并延长交  的延长线于点
的延长线于点  .
. 
-
(1) 求证:
 ∽
∽  ;
;
-
(2) 若正方形的边长为4,求
 的长.
的长.
如图,  的顶点都在方格纸的格点上,则
的顶点都在方格纸的格点上,则  .
.
 的顶点都在方格纸的格点上,则
的顶点都在方格纸的格点上,则  .
. 
反比例函数 的图象在( )
的图象在( )
 的图象在( )
的图象在( )
A . 第一、三象限
B . 第二、四象限
C . 第一、二象限
D . 第三、四象限
长方体的主视图与左视图如图所示(单位:cm),则其俯视图的面积是( )

A . 12cm2
B . 8cm2
C . 6cm2
D . 4cm2
如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是()

A . ∠ABP=∠C
B . ∠APB=∠ABC
C .  =
=  D .
D . 
 =
=  D .
D . 
如图,在边长为10的菱形ABCD中,AC为对角线,∠ABC=60°,M、N分别是边BC , CD上的点,BM=CN , 连接MN交AC于P点,当MN最短时,PC长度为.

如图,在平面直角坐标系中,过原点O及A(8,0)、C(0,6)作矩形OABC,连接AC,一个直角三角形PDE的直角顶点P始终在对角线AC上运动(不与A、C重合),且保持一边PD始终经过矩形顶点B,PE交x轴于点Q

-
(1)
 =;
=;
-
(2) 在点P从点C运动到点A的过程中,
 的值是否发生变化?如果变化,请求出其变化范围,如果不变,请说明理由,并求出其值;
的值是否发生变化?如果变化,请求出其变化范围,如果不变,请说明理由,并求出其值;
-
(3) 若将△QAB沿直线BQ折叠后,点A与点P重合,则PC的长为.
如图,几何体的俯视图是( )

A .  B .
B .  C .
C .  D .
D . 
如图是某个几何体的三视图,该几何体是( )
A . 正方体
B . 圆柱
C . 圆锥
D . 球
如图所示的几何体是由四个完全相同的正方体组成的,这个几何体的俯视图是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知三条线段的长分别是 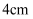 ,
,  和
和  ,则再加一条
,则再加一条  的线段,才能使之四条线段成比例.
的线段,才能使之四条线段成比例.
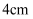 ,
,  和
和  ,则再加一条
,则再加一条  的线段,才能使之四条线段成比例.
的线段,才能使之四条线段成比例.
最近更新
- The teacher went into the classroom, ________the boy________
- 14、阅读下面这首唐诗,然后回答问题。(8分) 寻南溪常山道人隐居 刘长卿 一路经行处,莓苔见履痕。白云依静渚,春草
- 补写出下列名句名篇中的空缺部分。 (1)________________,除却巫山不是云。(元稹《离思》) (2)多情自
- 乙型肝炎病毒不能用动物细胞培养,无法用细胞培养的方法制造疫苗。自1979 年对乙型肝炎病毒基因组DNA测序完成后,已知病
- I won’t havea trip to Mount Huang unless Amy ____, either.
- 目前世界上能制造的芯片最小工艺水平是5纳米,而我国能制造芯片的最小工艺水平是16纳米,已知1纳米=米,用科学记数法将16
- 在热传递过程中,传递的多少叫做热量,热量单位是;热传递可以改变物体的,物体吸收热量,能增加.
- 有一个摆钟,它是依靠钟摆的摆动带动指针转动计时的。这个摆钟在地球上走得很准。现在将它带到某行星上,此行星的半径是地球半径
- 二战后,西方资本主义国家普遍进行政策调整,建立起包括医疗保健、养老、住房、失业保险和教育在内的“福利国家”制度。其主要目
- 已知函数f(x)=ax3+bx2-3x在x=±1处取得极值.(1)求函数f(x)的解析式;(2)求证:对于区间[-1,1
- 明朝统治者废除丞相、权分六部,设置厂卫特务机构,反映了 ( )①君主专制统治空前加强 ②对国家的行政管理更加有
- 下列各表述正确的是()A.图①表示在恒容容器中MgSO4(s) + CO(g)MgO(s) + CO2(g) + SO2
- 汶川大地震造成数万人死亡。在这场特大自然灾害面前灾区人民与全国人民一道众志成城,全力抗震救灾。请结合下图回答问题(8分)
- 下列词语中,没有错别字的一组是( ) A. 袒露 金榜提名 轻歌曼舞 文武之道,一张一弛 B.低俗
- 下列各组的电极材料和电解质溶液中,不能组成原电池的是 A.铜片,石墨棒,稀硫酸 B.铜片,石墨棒,硝酸
- 2013年5月27日,我国启动雪豹保护优先行动计划。为挽救濒危物种,保护生物多样性,一般不采用的措施是() A.建立自然
- 以前,我国东部经济快速发展引发了大规模的“移民潮”,未来我国中西部经济的发展将 使产业资本替代劳动力成为流动的主体,由“
- 新任深圳市副市长,代理市长职务的王荣,上任时表示:“堂堂正正、清清白白做人,扎扎实实、兢兢业业做事。一定自觉接受市委常委
- 近期一本财经图书《货币战争》名列畅销书榜首,但其中部分观点备受争议。该书作者把1929—1933年经济危机的爆发归结为国
- 无色的混合气体甲,可能含有NO、CO2、NO2、NH3、N2中的几种,将100 mL甲气体经过如图实验的处理,结果得到酸



