九年级(初三)数学下学期下册试题
已知平行四边形ABCD中,点E是边BC的中点,DE与AC相交于点F,设  =
=  ,
,  =
=  ,那么
,那么  =(用
=(用  ,
,  的式子表示)
的式子表示)
 =
=  ,
,  =
=  ,那么
,那么  =(用
=(用  ,
,  的式子表示)
的式子表示) 
如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于 .

如图,在四边形ABCD中,AD∥BC,∠A=∠BDC.

-
(1) 求证:△ABD∽△DCB;
-
(2) 若AB=12,AD=8,CD=15,求DB的长.
如图所示的几何体是由一些正方体组合而成的立体图形,则这个几何体的俯视图是
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在阳光下,身高1.6m的小强的影长是0.8m,同一时刻,一棵在树的影长为4.8m,则树的高度为( )
A . 4.8m
B . 6.4m
C . 9.6m
D . 10m
如图,在  中,
中,  ,
,  于点D,如果
于点D,如果  ,
,  ,那么
,那么  .
.
 中,
中,  ,
,  于点D,如果
于点D,如果  ,
,  ,那么
,那么  .
. 
已知反比例函数y= , 当x=2时,y=﹣
, 当x=2时,y=﹣ , 那么k等于( )
, 那么k等于( )
 , 当x=2时,y=﹣
, 当x=2时,y=﹣ , 那么k等于( )
, 那么k等于( )
A . 1
B . -1
C . -4
D . ﹣

于反比例函数 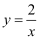 的图象,下列说法中,正确的是( )
的图象,下列说法中,正确的是( )
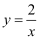 的图象,下列说法中,正确的是( )
的图象,下列说法中,正确的是( )
A . 图象的两个分支分别位于第二、第四象限
B . 图象的两个分支关于y轴对称
C . 图象经过点  D . 当
D . 当  时,y随x增大而减小
时,y随x增大而减小
 D . 当
D . 当  时,y随x增大而减小
时,y随x增大而减小
如图1是一副创意卡通圆规,图2是其平面示意图,OA是支撑臂,OB是旋转臂,使用时,以点A为支撑点,铅笔芯端点B可绕点A旋转作出圆.已知OA=OB=10cm.当∠AOB=18°.求所作圆的半径(结果精确到0.01 cm).
(参考数据:sin9°≈0.1564,cos9°≈0.9877,sin18°≈0.3090,cos18°≈0.9511)

如图,点A在双曲线y= (x>0)上,点B在双曲线y=
(x>0)上,点B在双曲线y= (x>0)上,
(x>0)上, 轴,分别过点A、B向x轴作垂线,垂足分别为D、C,若矩形ABCD的面积是15,则k的值为( )
轴,分别过点A、B向x轴作垂线,垂足分别为D、C,若矩形ABCD的面积是15,则k的值为( )
 (x>0)上,点B在双曲线y=
(x>0)上,点B在双曲线y= (x>0)上,
(x>0)上, 轴,分别过点A、B向x轴作垂线,垂足分别为D、C,若矩形ABCD的面积是15,则k的值为( )
轴,分别过点A、B向x轴作垂线,垂足分别为D、C,若矩形ABCD的面积是15,则k的值为( )
A . 21
B . 18
C . 15
D . 9
如图为一个正方体的表面展开图,则该正方体的六个表面中,与“善”字相对的面上的字是( )

A . 敬
B . 业
C . 诚
D . 信
正方体的截面不可能是( )
A . 四边形
B . 五边形
C . 六边形
D . 七边形
由6个相同的立方体搭成的几何体如图所示,则它的主视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在正方形网格中,cos∠ACB=.

如图,平面直角坐标系中,点A是x轴上任意一点,BC平行于x轴,分别交y=  (x>0)、y=
(x>0)、y=  (x<0)的图象于B、C两点,若△ABC的面积为2,则k的值为.
(x<0)的图象于B、C两点,若△ABC的面积为2,则k的值为.
 (x>0)、y=
(x>0)、y=  (x<0)的图象于B、C两点,若△ABC的面积为2,则k的值为.
(x<0)的图象于B、C两点,若△ABC的面积为2,则k的值为.

用计算器求下列各式的值:
-
(1) sin47°;
-
(2) sin12°30′;
-
(3) cos25°18′;
-
(4) tan44°59′59″;
-
(5) sin18°+cos55°﹣tan59°.
钓鱼岛自古就是中国的!2017年5月18日,中国海警2305,2308,2166,33115舰船队在中国的钓鱼岛领海内巡航,如图,我军以30km/h的速度在钓鱼岛A附近进行合法巡逻,当巡逻舰行驶到B处时,战士发现A在他的东北方向,巡逻舰继续向北航行40分钟后到达点C,发现A在他的东偏北15°方向,求此时巡逻舰与钓鱼岛的距离(  ≈1.414,结果精确到0.01)
≈1.414,结果精确到0.01)
 ≈1.414,结果精确到0.01)
≈1.414,结果精确到0.01)
如图,小华在晚上由路灯A走向路灯B.当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部;当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部.已知小华的身高是1.6m,两个路灯的高度都是9.6m,且AP=QB.

-
(1) 求两个路灯之间的距离;
-
(2) 当小华走到路灯B的底部时,他在路灯A下的影长是多少?
如图,某测量人员的眼睛A与标杆顶端F、电视塔顶端E在同一条直线上,已知此人的眼睛到地面的距离AB=1.6m,标杆FC=2.2m,且BC=1m,CD=5m,标杆FC、ED垂直于地面.求电视塔的高ED.

计算:  .
.
 .
.
最近更新
- 如图,矩形OABC的长OA为2,宽AB为1,则该矩形绕点O逆时 针旋90O后,B点的坐标为
- x﹣2[y+2x﹣(3x﹣y)].
- 已知Co2O3在酸性溶液中易被还原成Co2+,Co2O3、Cl2、FeCl3、I2的氧化性依次减弱。下列反应在水溶液中不
- ----- Would you like to have a taxi? ----- No, I _____ walk.
- 16.在下面一段文字横线处补写恰当的语句,每处不超过10个字。(5分) 礼是对人的社会行为的规范,是文明社会的重要
- 某人在乎直公路上骑自行车,见到前方较远处红色交通信号灯亮起,他便停止蹬车,此后的一段时间内,自行车前轮和后轮受到地面的摩
- 某反应2AB(g)C(g)+3D(g)在高温时能自发进行,其逆反应在低温下能自发进行,则该反应的正反应的△H、△S应为
- 某混合气体可能有CO、CO2、NH3、HCl、H2和水蒸气中的一种或几种,当依次通过澄清石灰水(无浑浊现象)、氢氧化钡溶
- cos的值为() A.- B. C. D.-
- 下列各句中没有语病的一句是A、科学分析表明,茶叶的含钾量特别高,夏天运动后,多喝茶可及时补充钾。B、香港国际电影节自成立
- 下列关于细胞增殖表述正确的是 ①二倍体动物体细胞有丝分裂后期,细胞每一极均含有同源染色体 ②二倍体
- 用2,3,4三个数字排成一个三位数,则排出的数是偶数的概率为
- 某“帆板”集训队在一海滨区域进行集训,该海滨区域的海浪高度(米)随着时间而周期性变化,每天各时刻的浪高数据的平均值如下表
- 下列句子中,标点符号使用正确的一句是( ) A.中国坚持把节约资源、保护环境作为基本国策,着力建设资源节约型、环
- 下列句子标点符号使用,完全正确的一项是 A、在语法方面, 古今也有不少差别。例如“我孰与城北徐公美?”就是古代特有的句法
- 1986年,人们成功的用如下反应制得了氟: ①2KMnO4+2KF+10HF+3H2O2=2K2MnF6+8H2O+3O
- 下列四项中哪个等级的生物共同特征最多?( ) A.门 B.属
- 计算: =_____
- 如图电路中,R为定值电阻,闭合开关后,当滑片P在某两点之间滑动时,电流表示数变化范围是0.5A~1.5A,电压表示数变化
- BUSSERVICE New York City — Brennan, New Jersey(Trip time:30



