九年级(初三)数学下学期下册试题
如图1,是全国最大的瓷碗造型建筑,座落于江西景德镇,整体造型概念来自“宋代影青斗笠碗”,造型庄重典雅,象征“万瓷之母”.小敏为了计算该建筑物横断面(瓷碗橫断面ABCD为等腰梯形)的高度,如图2,她站在与瓷碗底部AB位于同一水平面的点P处测得瓷碗顶部点D的仰角为45°,而后沿着一段坡度为0.44(坡面与水平线夹角的正切值)的小坡PQ步行到点Q(此过程中AD,AP,PQ始终处于同一平面)后测得点D的仰角减少了5°.已知坡面PQ的水平距离为20米,小敏身高忽略不计,试计算该瓷碗建筑物的高度.(参考数据:sin 40°≈0.64,tan 40°≈0.84)

已知点A(1,-3)关于x轴的对称点A'在反比例函数  的图像上,则实数k的值为( )
的图像上,则实数k的值为( )
 的图像上,则实数k的值为( )
的图像上,则实数k的值为( )
A . 3
B .  C . -3
D .
C . -3
D . 
 C . -3
D .
C . -3
D . 
如图,A、B两点在河的两岸,要测量这两点之间的距离,测量者在与A同侧的河岸边选定一点C,测出AC=a米,∠A=90°,∠C=40°,则AB等于( )米.

A . asin40°
B . acos40°
C . atan40°
D . 

某新农村乐园设置了一个秋千场所,如图所示,秋千拉绳OB的长为3m,静止时,踏板到地面距离BD的长为0.6m(踏板厚度忽略不计).为安全起见,乐园管理处规定:儿童的“安全高度”为hm,成人的“安全高度”为2m(计算结果精确到0.1m)

-
(1) 当摆绳OA与OB成45°夹角时,恰为儿童的安全高度,则h=m
-
(2) 某成人在玩秋千时,摆绳OC与OB的最大夹角为55°,问此人是否安全?(参考数据:
 ≈1.41,sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
≈1.41,sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
如图,△ABC中,BD和CE是两条高,如果∠A=45°,则  =.
=.
 =.
=. 
如图,直立在点  处的标杆
处的标杆  长
长  ,站立在点
,站立在点  处的观察者从点
处的观察者从点  处看到标杆顶
处看到标杆顶  、旗杆顶
、旗杆顶  在一条直线上.已知
在一条直线上.已知  ,
,  ,
,  ,求旗杆高
,求旗杆高  .
.
 处的标杆
处的标杆  长
长  ,站立在点
,站立在点  处的观察者从点
处的观察者从点  处看到标杆顶
处看到标杆顶  、旗杆顶
、旗杆顶  在一条直线上.已知
在一条直线上.已知  ,
,  ,
,  ,求旗杆高
,求旗杆高  .
. 
如果二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=bx+c和反比例函数y= 在同一坐标系中的图象大致是( )
在同一坐标系中的图象大致是( )

A . 
B .
B .  C .
C . 
D .
D . 

B .
B .  C .
C . 
D .
D . 
若点  都在反比例函数
都在反比例函数  的图象上,则
的图象上,则  的大小关系是( )
的大小关系是( )
 都在反比例函数
都在反比例函数  的图象上,则
的图象上,则  的大小关系是( )
的大小关系是( )
A .  B .
B .  C .
C .  D .
D . 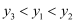
 B .
B .  C .
C .  D .
D . 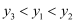
计算:

周末小明和同学们去“绿博园”的枫湖坐船,观赏风景;如图,小明正在A处的小船上,B处小船上的游客发现点A在点B的正西方向上,C处小船上的游客发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距120米.

-
(1) 求出此时点A到点C的距离;
-
(2) 若小明从A处沿AC方向向C驶去,当到达点A′时,测得点B在A′的南偏东75°的方向上,求此时小明所乘坐的小船走的距离.(注:结果保留根号)
如图,P是△ABC的重心,过点P作PE∥AB交BC于点E,PF∥AC交BC于点F,若△PEF的周长是6,则△ABC的周长为.

如图,  的直径
的直径  垂直于弦
垂直于弦  ,垂足为
,垂足为  ,
,  ,
,  ,则
,则  的长为( )
的长为( )
 的直径
的直径  垂直于弦
垂直于弦  ,垂足为
,垂足为  ,
,  ,
,  ,则
,则  的长为( )
的长为( ) 
A . 2.5
B . 4
C . 5
D . 10
如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10米,∠B=36°,则中柱AD(D为底边中点)的长是( )

A . 5sin36°米
B . 5cos36°米
C . 5tan36°米
D . 10tan36°米
如图,点B、D、C、F在一条直线上,且  ,
,  ,求证:
,求证:  .
.
 ,
,  ,求证:
,求证:  .
. 
如图,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且BD=  BA,则
BA,则  的值为( )
的值为( )
 BA,则
BA,则  的值为( )
的值为( )
A .  B .
B .  C .
C . 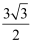 D .
D . 
 B .
B .  C .
C . 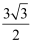 D .
D . 
若函数  的图象过点
的图象过点  ,则此函数图象位于( )
,则此函数图象位于( )
 的图象过点
的图象过点  ,则此函数图象位于( )
,则此函数图象位于( )
A . 第一、二象限
B . 第一、三象限
C . 第二、三象限
D . 第二、四象限
已知圆锥的底面半径为3cm,高为4cm,则这个圆锥的侧面积为。
如图,在下列方格纸中的四个三角形,是相似三角形的是( )

A . ①和②
B . ①和③
C . ②和③
D . ②和④
如图,某同学参加社会实践活动,站在甲、乙两栋楼中间,看甲楼顶部A的仰角为60°,看乙楼顶部C的仰角为45°,已知乙楼的高度为41.5米,该同学的的身高为1.5米.求甲楼AB的高度.(结果保留根号)

在水平的讲台上放置圆柱形水杯和长方体形粉笔盒(如图),则从正面看得到的平面图形是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B . 最近更新
- 某鸭梨产区建立恒温库储存鸭梨,为反季节销售提供了条件,也为梨农增收提供了保障,据测算,每储存1千克鸭梨可增加收入0.5元
- 下列有关“中国地理位置”的说法,正确的是( ) A. 从南、北半球看,中国位于南半球 B. 从东、西半球看,中国位于西
- 康有为说“布衣改制,事大骇人,故不如托之先王,既不惊人,又可避祸。”这句话反映的实质问题是 A.康有为认为改制代表平民利
- The most important _____ of his speech was that we should al
- How do you ________ these naughty children? A. do with B
- 填入下列一段文字中横线处的语句,与上下文衔接最恰当的一组是 不是所有的欢笑都表达了高兴,就像______________
- The other day,my friend Jane was invited to a 40th birthday
- Under good treatment, Linda is beginning to _________ and wi
- 正整数按如图的规律排列,请写出第15行,第17列的数字是()A.271 B.270 C.256 D.255
- 把太阳系各行星的轨迹近似的看作匀速圆周运动,则离太阳越远的行星() A. 周期越小
- 下列中央官制形成的先后顺序是 ①三公九卿制 ②三省六部制 ③内阁制 ( )
- 在ABC中,角A、B、C 所对的边分别为 ,cos2C+2cosC+2=0. (Ⅰ)求角C的大小; (Ⅱ)若b
- 阅读下列短文,根据短文内容完成表格中所缺信息,每空一词。Street Markets Around the WorldT
- 图4为近年来影响我国耕地减少的因素构成图。读图,完成下列各题。图中因素对农业用地造成实质性减少的有 A.①② B.②
- 在如图甲所示的电路中,L 1、L 2和L3为三个相同规格的小灯泡,这种小灯泡的伏安特性曲线如图乙所示,当开关S闭合后,电
- 图所示是王濛在2010年温哥华冬奥会500米短道速滑比赛中夺金的场景。在滑行的过程中,冰刀与冰面之间的摩擦为______
- 如图所示,实线是一个电场中的电场线,虚线是一个负检验电荷在这个电场中的轨迹,若电荷是从a处运动到b处,以下判断正确的是
- 明朝永乐帝时设立了内阁制,以内阁作为皇帝处理国政的助理机构。英国“光荣革命”之后,国王威廉三世逐渐以内阁代替枢密院,成为
- 真正的哲学是指( ) A.将一切具体科学包括在内的哲学 B.马克思主义哲学 C.正确反映时代本质要求的哲学
- 如图所示,带箭头的线段表示某一电场的电场线,在电场力作用下(不计重力)一带电粒子经过A点飞向B点,径迹如图中虚线所示,以



