九年级(初三)数学下学期下册试题
若相似△ABC与△DEF的相似比为1:3,则△ABC与△DEF的面积比为( )
A . 1:3
B . 1:9
C . 3:1
D . 1: 

如图,现有一个圆心角为90°,半径为8cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为( )

A . 4cm
B . 3cm
C . 2cm
D . 1cm
已知:如图,在Rt△ABC和Rt△BCD中,∠ABC=∠BCD=90°,BD与AC相交于点E,AB=9,cos∠BAC=  ,tan∠DBC=
,tan∠DBC= 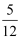 .
.
 ,tan∠DBC=
,tan∠DBC= 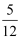 .
. 
求:
-
(1) 边CD的长;
-
(2) △BCE的面积.
右图中曲线是反比例函数  的图象的一支.
的图象的一支.

-
(1) 这个反比例函数图象的另一支位于哪个象限?常数n的取值范围是什么?
-
(2) 若一次函数
 的图象与反比例函数的图象交于点A,与x轴交于点B,△AOB的面积为2,求n的值.
的图象与反比例函数的图象交于点A,与x轴交于点B,△AOB的面积为2,求n的值.
如图分别是某款篮球架的实物图与示意图,已知  于点
于点  ,底座
,底座  的长为1米,底座
的长为1米,底座  与支架
与支架  所成的角
所成的角  ,点
,点  在支架
在支架 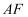 上,篮板底部支架
上,篮板底部支架  于点
于点  ,已知
,已知  长
长  米,
米,  长
长  米,
米,  长1米.
长1米.
 于点
于点  ,底座
,底座  的长为1米,底座
的长为1米,底座  与支架
与支架  所成的角
所成的角  ,点
,点  在支架
在支架 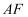 上,篮板底部支架
上,篮板底部支架  于点
于点  ,已知
,已知  长
长  米,
米,  长
长  米,
米,  长1米.
长1米. 
-
(1) 求篮板底部支架
 与
与 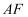 支架所成的角
支架所成的角  的度数.
的度数.
-
(2) 求篮板底部点
 到地面的距离.(结果保留根号)
到地面的距离.(结果保留根号)
如图,在△ABC中,AC=8厘米,BC=16厘米,点P从点A出发,沿着AC边向点C以1cm/s的速度运动,点Q从点C出发,沿着CB边向点B以2cm/s的速度运动,如果P与Q同时出发,经过几秒△PQC和△ABC相似?

在平面直角坐标系中,点A  点B
点B  已知
已知  满足
满足  .
.
 点B
点B  已知
已知  满足
满足  .
. 
-
(1) 点A的坐标为,点B的坐标为;
-
(2) 如图1,点E为线段OB上一点,连接AE,过A作AF⊥AE,且AF=AE,连接BF交
 轴于点D,若点D(-1,0),求点E的坐标;
轴于点D,若点D(-1,0),求点E的坐标;
-
(3) 在(2)的条件下,如图2,过E作EH⊥OB交AB于H,点M是射线EH上一点(点M不在线段EH上),连接MO,作∠MON=45°,ON交线段BA的延长线于点N,连接MN,探究线段MN与OM的关系,并说明理由。
如图,以Rt△ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E为OB的中点,连接CE并延长交⊙O于点F,点F恰好落在  的中点,连接AF并延长与CB的延长线相交于点G,连接OF.
的中点,连接AF并延长与CB的延长线相交于点G,连接OF.

-
(1) 求证:OF=
 BG;
BG;
-
(2) 若AB=4,求DC的长.
一个几何体由大小相同的小立方块搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请画出从正面和从左面看到的这个几何体的形状图。



如图,∠ADE=∠ACD=∠ABC,图中相似三角形共有( )

A . 1对
B . 2对
C . 3对
D . 4对
已知点  ,
,  在反比例函数
在反比例函数 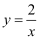 上,当
上,当  时,
时,  ,
,  的大小关系是.
的大小关系是.
 ,
,  在反比例函数
在反比例函数 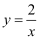 上,当
上,当  时,
时,  ,
,  的大小关系是.
的大小关系是.
如图,已知甲地在乙地的正东方向,因有大山阻隔,由甲地到乙地需要绕行丙地.已知丙地位于甲地北偏西  方向,距离甲地
方向,距离甲地  ,丙地位于乙地北偏东
,丙地位于乙地北偏东  方向,现要打通穿山隧道,建成甲乙两地直达高速公路,如果将甲、乙、丙三地当作三个点
方向,现要打通穿山隧道,建成甲乙两地直达高速公路,如果将甲、乙、丙三地当作三个点 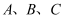 ,可抽象成右图所示的三角形,求甲乙两地之间直达高速线路的长
,可抽象成右图所示的三角形,求甲乙两地之间直达高速线路的长  (结果用含非特殊角的三角函数和根式表示即可).
(结果用含非特殊角的三角函数和根式表示即可).
 方向,距离甲地
方向,距离甲地  ,丙地位于乙地北偏东
,丙地位于乙地北偏东  方向,现要打通穿山隧道,建成甲乙两地直达高速公路,如果将甲、乙、丙三地当作三个点
方向,现要打通穿山隧道,建成甲乙两地直达高速公路,如果将甲、乙、丙三地当作三个点  ,可抽象成右图所示的三角形,求甲乙两地之间直达高速线路的长
,可抽象成右图所示的三角形,求甲乙两地之间直达高速线路的长  (结果用含非特殊角的三角函数和根式表示即可).
(结果用含非特殊角的三角函数和根式表示即可).

如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且DE∥BC,EF∥A
B.若AD=2BD,则  的值为( )
的值为( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,已知△AOB与△A1OB1是以点O为位似中心的位似图形.且相似比为1:2,点B的坐标为(﹣2,4),则点B1的坐标为( )

A . (4,﹣8)
B . (2,﹣4)
C . (﹣1,8)
D . (﹣8,4)
如图是由5个大小相同的正方体搭成的几何体,则这个几何体的主视图是( )

A .  B .
B .  C .
C .  D .
D . 
 D .
D . 
如图,在平行四边形ABCD中, , 过点B作
, 过点B作 于E,连结AE,
于E,连结AE, , F为AE上一点,且
, F为AE上一点,且 .
.
 , 过点B作
, 过点B作 于E,连结AE,
于E,连结AE, , F为AE上一点,且
, F为AE上一点,且 .
. 
-
(1) 求证:
 .
.
-
(2) BF的长为.
双曲线  、
、  在第一象限的图象如图,
在第一象限的图象如图,  ,过
,过  上的任意一点
上的任意一点  ,作
,作  轴的平行线交
轴的平行线交  于
于  ,交
,交  轴于
轴于  ,若
,若  ,则
,则  的解析式是.
的解析式是.
 、
、  在第一象限的图象如图,
在第一象限的图象如图,  ,过
,过  上的任意一点
上的任意一点  ,作
,作  轴的平行线交
轴的平行线交  于
于  ,交
,交  轴于
轴于  ,若
,若  ,则
,则  的解析式是.
的解析式是. 
如图,从点A看一山坡上的电线杆PQ,观测点P的仰角是45°,向前走6m到达B点,测得顶端点P和杆底端点Q的仰角分别是60°和30°,求该电线杆PQ的高度.

如图所示的正方体展开后的平面图形是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在△ABC中,∠C=90°,sinA= , 则sinB的值是( )
, 则sinB的值是( )
 , 则sinB的值是( )
, 则sinB的值是( )
A .  B .
B . 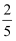 C .
C .  D .
D . 
 B .
B . 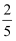 C .
C .  D .
D . 
最近更新
- 下列有关化学反应速率及限度的描述错误的是 A.催化剂能改变化学反应的速率B.一定条件下的可逆反应,反应物的转化率不可能
- 在新型飞机的研制中,将飞机模型放在风洞中固定不动,让风(高速流动的空气)迎面吹来,可以模拟飞机在空中的飞行情况.在此情境
- 5的相反数是 A. B.5
- 读我国部分地区风能密度分布图回答下列问题。(1)风能作为新能源的优点是什么? (2)分析图示地区风能密度在沿海最大的原因
- 我国宪法规定:“中华人民共和国的一切权力属于人民。人民行使国家权力的机关是全国人民代表大会和地方各级人民代表大会。”这说
- 下列实验不能达到目的的是 ( )
- 我国很早就掌握了养蚕、编织丝绸等技术。其中有一道工序是将蚕茧用热水浸泡后缫丝,此时茧内的家蚕发育成( ) A.卵
- The retired couple enjoy__________ photos.They always go out
- (09年山东猜题卷)已知是等差数列,,,则过点P (3 ,) ,Q(4 ,)的直线的斜率为 ( ) A.
- 阅读下列材料,回答问题。 材料一 现代化是人类社会的一次转型,是文明方式的一次转换,现代化用工业生产力取代农业生产力,在
- ,春风不度玉门关。
- 根据实验目的进行生物工程设计,下表中所选择的实验材料及材料特点错误的有几项()组别 实验目的 实验材料 材料特点 1 动
- 阅读下面的文字,完成下面试题目。 诗歌、神话传说和天文学(节选) 在古代的传说中,阏伯和实沈的故事是具有天文背景的一个。
- 性状分离是指() A.杂合子后代表现出相对性状的不同类型 B.染色体的分离 C.遗传因子的分离 D.以上说法都对
- 建国60年来,我国居民在不同的时代,结婚“三大件”是不断变化的。从手表、自行车、缝纫机,到冰箱、彩电、洗衣机,到如今的房
- 建国前30年,我国外交的关键词是结盟外交、斗争外交和革命外交。20世纪八十年代以来,合作外交、融入外交与和平外交成为我国
- 对于大于1的自然数m的n次幂可用奇数进行 如图所示的“分裂”,仿此,记53的“分裂”中 的最
- 多边形的一个顶点的所有对角线把多边形分成12个三角形,则这个多边形的边数是( ) A.12
- 【公民道德与伦理常识】 2009年12月7日,联合国气候变化大会在丹麦首都哥本哈根召开,会议就《京都议定书》第一
- 下图为人体体液物质交换示意图,其中正确的叙述为 ( )A. A、B、C依次为血浆、组织液、淋巴 B. A、B



