九年级(初三)数学下学期下册试题
一个圆锥的三视图如图,则此圆锥的表面积为.

如图,AB和DE是直立在地面上的两根立柱.AB=5m,某一时刻AB在阳光下的投影BC=3m,同时测量出DE在阳光下的投影长为6m.

-
(1) 请你在图中画出此时DE在阳光下的投影;
-
(2) 请你计算DE的长.
如图所示,一辆单车放在水平的地面上,车把头下方 处与坐垫下方
处与坐垫下方 处在平行于地面的同一水平线上,
处在平行于地面的同一水平线上, ,
,  之间的距离约为
之间的距离约为 , 现测得
, 现测得 ,
,  与
与 的夹角分别为
的夹角分别为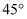 与
与 , 若点
, 若点 到地面的距离
到地面的距离 为
为 , 坐垫中轴
, 坐垫中轴 处与点
处与点 的距离
的距离 为
为 , 求点
, 求点 到地面的距离(结果保留一位小数).(参考数据:
到地面的距离(结果保留一位小数).(参考数据: ,
,  ,
,  )
)
 处与坐垫下方
处与坐垫下方 处在平行于地面的同一水平线上,
处在平行于地面的同一水平线上, ,
,  之间的距离约为
之间的距离约为 , 现测得
, 现测得 ,
,  与
与 的夹角分别为
的夹角分别为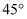 与
与 , 若点
, 若点 到地面的距离
到地面的距离 为
为 , 坐垫中轴
, 坐垫中轴 处与点
处与点 的距离
的距离 为
为 , 求点
, 求点 到地面的距离(结果保留一位小数).(参考数据:
到地面的距离(结果保留一位小数).(参考数据: ,
,  ,
,  )
)
已知点A在反比例函数  的图象上,AB⊥y轴,点C在x轴上,S△ABC=2,则反比例函数的解析式为.
的图象上,AB⊥y轴,点C在x轴上,S△ABC=2,则反比例函数的解析式为.
 的图象上,AB⊥y轴,点C在x轴上,S△ABC=2,则反比例函数的解析式为.
的图象上,AB⊥y轴,点C在x轴上,S△ABC=2,则反比例函数的解析式为.
如图,反比例函数y=  (x<0)的图象经过点P,则k的值为.
(x<0)的图象经过点P,则k的值为.
 (x<0)的图象经过点P,则k的值为.
(x<0)的图象经过点P,则k的值为. 
如图,在▱ABCD中,M、N为BD的三等分点,连接CM并延长交AB与点E,连接EN并延长交CD于点F,则DF:FC等于( ).

A . 1:2
B . 1:3
C . 2:3
D . 1:4
如图,在△ABC中,DE∥BC,  ,则下列结论中正确的是( )
,则下列结论中正确的是( )
 ,则下列结论中正确的是( )
,则下列结论中正确的是( ) 
A .  B .
B .  C .
C .  D .
D . 
如图,一次函数  的图象与反比例函数
的图象与反比例函数  的图象分别交于第二、四象限的A,B两点,点A的横坐标为
的图象分别交于第二、四象限的A,B两点,点A的横坐标为  .
.
 的图象与反比例函数
的图象与反比例函数  的图象分别交于第二、四象限的A,B两点,点A的横坐标为
的图象分别交于第二、四象限的A,B两点,点A的横坐标为  .
. 
-
(1) 求反比例函数的表达式;
-
(2) 根据图象回答:当x取何值时,
 请直接写出答案:.
请直接写出答案:.
tan30°=.
小明的身高是  米,他的影长是
米,他的影长是  米,同一时刻古塔的影长是
米,同一时刻古塔的影长是  米,则古塔的高是米.
米,则古塔的高是米.
如图,是由两个正方体组成的几何体,则该几何体的左视图为( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,过x轴上任意一点P作y轴的平行线,分别与反比例函数y=  (x>0),y=﹣
(x>0),y=﹣ 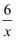 (x>0)的图象交于A点和B点,若C为y轴任意一点.连接AB、BC,则△ABC的面积为.
(x>0)的图象交于A点和B点,若C为y轴任意一点.连接AB、BC,则△ABC的面积为.
 (x>0),y=﹣
(x>0),y=﹣ 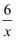 (x>0)的图象交于A点和B点,若C为y轴任意一点.连接AB、BC,则△ABC的面积为.
(x>0)的图象交于A点和B点,若C为y轴任意一点.连接AB、BC,则△ABC的面积为. 
-
(1) 计算:
 .
.
-
(2) 先化简,再求值:
 ,其中
,其中 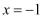 .
.
阅读下面材料:如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2=  交于A(1,3)和B(﹣3,﹣1)两点,观察图象可知:①当x=﹣3或1时,y1=y2;②当﹣3<x<0或x>1时,y1>y2;即通过观察函数的图象,可以得到不等式ax+b>
交于A(1,3)和B(﹣3,﹣1)两点,观察图象可知:①当x=﹣3或1时,y1=y2;②当﹣3<x<0或x>1时,y1>y2;即通过观察函数的图象,可以得到不等式ax+b>  的解集.
的解集.
 交于A(1,3)和B(﹣3,﹣1)两点,观察图象可知:①当x=﹣3或1时,y1=y2;②当﹣3<x<0或x>1时,y1>y2;即通过观察函数的图象,可以得到不等式ax+b>
交于A(1,3)和B(﹣3,﹣1)两点,观察图象可知:①当x=﹣3或1时,y1=y2;②当﹣3<x<0或x>1时,y1>y2;即通过观察函数的图象,可以得到不等式ax+b>  的解集.
的解集.

有这样一个问题:求不等式x3+4x2﹣x﹣4>0的解集.
艾斯柯同学类比以上知识的研究方法,用函数与方程的思想对不等式的解法进行了探究,请将他下面的②③④补充完整:
①当x=0时,原不等式不成立:当x>0时,原不等式可以转化为x2+4x﹣1>  ;当x<0时,原不等式可以转化为x2+4x﹣1<
;当x<0时,原不等式可以转化为x2+4x﹣1<  .
.
②构造函数,画出图象
设y3=x2+4x﹣1,y4=  在同一坐标系中分别画出这两个函数的图象.
在同一坐标系中分别画出这两个函数的图象.
双曲线y4=  如图2所示,请在此坐标系中直接画出抛物线y3=x2+4x﹣1(可不列表);
如图2所示,请在此坐标系中直接画出抛物线y3=x2+4x﹣1(可不列表);

③利用图象,确定交点横坐标
观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为 
④借助图象,写出解集
结合(1)的讨论结果,观察两个函数的图象可知:不等式x3+4x2﹣x﹣4>0的解集为 
综合题
-
(1) 如图1,锐角△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE交于F,连DE,求证:DF•DA=DB•DC;

-
(2) 如图2,若∠BAC=90°,AD⊥BC于D,F为线段AD上一点,在AD延长线上找一点G使AD2=DF•DG,请画出图形找出点G并加以证明;

-
(3) 如图3,在(1)的条件下,若∠ABC=45°,EF=1,EC=3,直接写出BD长.

如图,在平面直角坐标系中,直线  过点
过点  ,过点A作x轴的垂线,垂足为点B,过点A作y轴的垂线,垂足为点C.
,过点A作x轴的垂线,垂足为点B,过点A作y轴的垂线,垂足为点C. 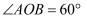 ,
,  于点D.动点P从点O出发,以每秒2个单位长度的速度向点A运动,动点Q从点A出发.以每秒
于点D.动点P从点O出发,以每秒2个单位长度的速度向点A运动,动点Q从点A出发.以每秒  个单位长度的速度向点B运动.点P,Q同时开始运动,当点P到达点A时,点P,Q同时停止运动,设运动时间为
个单位长度的速度向点B运动.点P,Q同时开始运动,当点P到达点A时,点P,Q同时停止运动,设运动时间为  ,且
,且  .
.
 过点
过点  ,过点A作x轴的垂线,垂足为点B,过点A作y轴的垂线,垂足为点C.
,过点A作x轴的垂线,垂足为点B,过点A作y轴的垂线,垂足为点C. 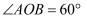 ,
,  于点D.动点P从点O出发,以每秒2个单位长度的速度向点A运动,动点Q从点A出发.以每秒
于点D.动点P从点O出发,以每秒2个单位长度的速度向点A运动,动点Q从点A出发.以每秒  个单位长度的速度向点B运动.点P,Q同时开始运动,当点P到达点A时,点P,Q同时停止运动,设运动时间为
个单位长度的速度向点B运动.点P,Q同时开始运动,当点P到达点A时,点P,Q同时停止运动,设运动时间为  ,且
,且  .
. 
-
(1) 求m与k的值;
-
(2) 当点P运动到点D时,求t的值;
-
(3) 连接DQ,点E为DQ的中点,连接PE,当
 时,请直接写出点P的坐标.
时,请直接写出点P的坐标.
知识改变世界,科技改变生活。导航设备的不断更新方便了人们的出行。如图,某校组织学生乘车到蒲江茶叶基地C地进行研学活动,车到达A地后,发现C地恰好在A地的正东方向,且距A地9.1千米,导航显示车辆应沿南偏东60°方向行驶至B地,再沿北偏东53°方向行驶一段距离才能到达C地,求B、C两地的距离(精确到个位)
(参考数据  )
)

如图,伞不论张开还是收紧,伞柄AP始终平分同一平面内两条伞架所成的角∠BAC,当伞收紧时,结点D与点M重合,且点A、E、D在同一条直线上,已知部分伞架的长度如下:单位:cm
伞架 | DE | DF | AE | AF | AB | AC |
长度 | 36 | 36 | 36 | 36 | 86 | 86 |

-
(1) 求AM的长.
-
(2) 当∠BAC=104°时,求AD的长(精确到1cm).
备用数据:sin52°=0.788,cos52°=0.6157,tan52°=1.2799.
如图是由6个大小相同的立方体组成的几何体,在这个几何体的三视图中,是中心对称图形的是( )

A . 主视图
B . 左视图
C . 俯视图
D . 主视图和左视图
几个棱长为1的正方体组成几何体的三视图如图,则这个几何体的体积是( )

A . 5
B . 6
C . 7
D . 8
最近更新
- 每年的7月11日被定位“世界人口日”,人口问题越来越受到国际社会的重视,下图表示三种可能的人口增长曲线,请回答: (1)
- 如图16-3-8所示,两个质量均为4m的小球A和B由轻弹簧连接,置于光滑水平面上.一颗质量为m子弹,以水平速度v0射入A
- 哥伦布在《哥伦布致西班牙国王和王后书》中写道“陛下可以统治此间……人们可在这里获得黄金……但我以为陛下最好不采用掳掠的方
- 下列词语中,没有错别字的一项是 A、跑酷 擎天柱 过渡政府 涸泽而鱼 B、
- 几年前,北京景山公园成立了老年合唱团。每天清晨,老人们聚在一起练习唱歌.他们演唱的大多是革命歌曲,在激昂的歌声中,老人们
- We had a really bad time about six months ago but now things
- 把平面图形上的所有点在一个平面上的射影构成的图形叫做图形在这个平面上的射影,如图,在长方体中,,,,则在平面上的射影的面
- 用显微镜观察洋葱表皮细胞时,由低倍镜换成高倍镜后发现 ( ) A.视野变暗 细胞数
- 历史上著名的“澶渊之盟”反映了北宋与少数民族政权之间的关系,这个政权属于 A.契丹族 B.突厥族 C.吐蕃族 D.党项族
- 读我国某大城市南郊1996~2006年部分土地利用变化数据表,回答下列各题。13.表中缺少的土地利用类型最可能是 A.
- Hearingthe old man’s report, the officer _______ from his se
- Plants arevery important living things. Life could not go on
- 某反应2A+B=C+3D,若25gA与10gB恰好完全反应生成5gC,那么生成6gD时参加反应的A是() A.5gB.1
- 某有机物,它的蒸气密度是相同条件下空气密度的2.56倍。11.1g该有机物充分燃烧后的产物通过浓硫酸后增重8.1g,剩余
- 就上述冲突的调解,应由下列哪个组织进行?( ) A.欧盟 B.世界贸易组织 C.联合国
- 对化学变化描述不正确的是A.有新物质生成B.分子可以分为原子C.有颜色变化 D.分子变成其它分子
- 下面是《琵琶行》中的五个名句,它们在诗中出现的先后顺序为( ) ①千呼万唤始出来,犹抱琵琶半遮面。 ②同是天涯
- 书法艺术是中华民族创造的一种独特的艺术形式,已有几千年的历史。要继承这一传统文化,发挥它的积极作用,人们应该具有的正确态
- A、B两小球同时从距地面高为h=15 m处的同一点抛出,初速度大小均为v0=10 m/s.A球竖直向下抛出,B球水平抛出
- Do youwant to be productive(富有成效的)at work or at home? Here's



