九年级(初三)数学下学期下册试题
其几何体的三视图如图所示,这个几何体是( )

A . 三棱柱
B . 四棱锥
C . 四棱柱
D . 圆锥
某移动公司为了提升网络信号,在坡度  的山坡
的山坡  上加装了信号塔
上加装了信号塔  (如图所示),信号塔底端Q到坡底A的距离为3.9米.为了提醒市民,在距离斜坡底A点5.4米的水平地面上立了一块警示牌
(如图所示),信号塔底端Q到坡底A的距离为3.9米.为了提醒市民,在距离斜坡底A点5.4米的水平地面上立了一块警示牌  ,当太阳光线与水平线所成的夹角为
,当太阳光线与水平线所成的夹角为 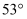 时,信号塔顶端P的影子落在警示牌上的点E处,且
时,信号塔顶端P的影子落在警示牌上的点E处,且  长为3米.
长为3米.
 的山坡
的山坡  上加装了信号塔
上加装了信号塔  (如图所示),信号塔底端Q到坡底A的距离为3.9米.为了提醒市民,在距离斜坡底A点5.4米的水平地面上立了一块警示牌
(如图所示),信号塔底端Q到坡底A的距离为3.9米.为了提醒市民,在距离斜坡底A点5.4米的水平地面上立了一块警示牌  ,当太阳光线与水平线所成的夹角为
,当太阳光线与水平线所成的夹角为 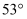 时,信号塔顶端P的影子落在警示牌上的点E处,且
时,信号塔顶端P的影子落在警示牌上的点E处,且  长为3米.
长为3米. 
-
(1) 求点Q到水平地面的铅直高度;
-
(2) 求信号塔
 的高度大约为多少米?(参考数据:
的高度大约为多少米?(参考数据:  )
)
如图,在  中,下列所给的四个条件,其中不一定能得到
中,下列所给的四个条件,其中不一定能得到  的条件是( )
的条件是( )
 中,下列所给的四个条件,其中不一定能得到
中,下列所给的四个条件,其中不一定能得到  的条件是( )
的条件是( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,Rt△ABC中,∠ACB=90°,  ,
,  ,将边
,将边  沿
沿 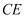 翻折,使点
翻折,使点  落在
落在  上的点
上的点  处;再将边
处;再将边  沿
沿 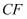 翻折,使点
翻折,使点  落在
落在  的延长线上的点
的延长线上的点 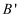 处,两条折痕与斜边
处,两条折痕与斜边  分别交于点
分别交于点  、
、  ,则线段
,则线段  的长为( )
的长为( )
 ,
,  ,将边
,将边  沿
沿 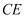 翻折,使点
翻折,使点  落在
落在  上的点
上的点  处;再将边
处;再将边  沿
沿 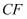 翻折,使点
翻折,使点  落在
落在  的延长线上的点
的延长线上的点 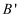 处,两条折痕与斜边
处,两条折痕与斜边  分别交于点
分别交于点  、
、  ,则线段
,则线段  的长为( )
的长为( ) 
A . 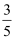 B .
B . 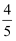 C .
C . 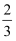 D .
D . 
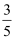 B .
B . 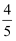 C .
C . 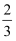 D .
D . 
小明乘车从姜堰到泰州,行车的平均速度y(km/h)和行车时间x(h)之间的函数图象是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,小伟在打网球时,击球点距离球网的水平距离是8米.已知网高是0.8米,要使球恰好能打过网,且落在离网4米的位置,则球拍击打的高度h为( )
![]()
A . 1.0
B . 1.6
C . 2.0
D . 2.4
已知一次函数 的图像如图所示,则二次函数
的图像如图所示,则二次函数 和反比例函数
和反比例函数 在同一坐标系内的图象可能是( )
在同一坐标系内的图象可能是( )
 的图像如图所示,则二次函数
的图像如图所示,则二次函数 和反比例函数
和反比例函数 在同一坐标系内的图象可能是( )
在同一坐标系内的图象可能是( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知:如图,在 中,
中, ,
, 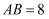 cm,
cm, cm,
cm, 为
为 边上的高,点
边上的高,点 从点
从点 出发,沿
出发,沿 方向匀速运动,速度为
方向匀速运动,速度为 cm/s;同时,点
cm/s;同时,点 从点
从点 出发,沿
出发,沿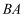 方向匀速运动,速度为
方向匀速运动,速度为 cm/s.设运动时间为
cm/s.设运动时间为 .
.
 中,
中, ,
, 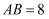 cm,
cm, cm,
cm, 为
为 边上的高,点
边上的高,点 从点
从点 出发,沿
出发,沿 方向匀速运动,速度为
方向匀速运动,速度为 cm/s;同时,点
cm/s;同时,点 从点
从点 出发,沿
出发,沿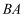 方向匀速运动,速度为
方向匀速运动,速度为 cm/s.设运动时间为
cm/s.设运动时间为 .
. 解答下列问题:

-
(1) 当
 为何值时,
为何值时, ;
;
-
(2) 当
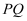 中点在
中点在 上时,求
上时,求 的值;
的值;
-
(3) 设四边形
 的面积为
的面积为 , 求
, 求 与
与 的函数关系式,并求
的函数关系式,并求 最小值;
最小值;
-
(4) 是否存在某一时刻
 , 使得
, 使得 , 若存在,求出
, 若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
如图,A,B,C三点在⊙O上,直径BD平分∠ABC,过点D作DE∥AB交弦BC于点E,过点D作⊙O的切线交BC的延长线于点F.

-
(1) 求证:EF=ED;
-
(2) 如果半径为5,cos∠ABC=
 ,求DF的长.
,求DF的长.
已知点P(﹣3,2),点Q(2,a)都在反比例函数y=  (k≠0)的图象上,过点Q分别作两坐标轴的垂线,两垂线与两坐标轴围成的矩形面积为( )
(k≠0)的图象上,过点Q分别作两坐标轴的垂线,两垂线与两坐标轴围成的矩形面积为( )
 (k≠0)的图象上,过点Q分别作两坐标轴的垂线,两垂线与两坐标轴围成的矩形面积为( )
(k≠0)的图象上,过点Q分别作两坐标轴的垂线,两垂线与两坐标轴围成的矩形面积为( )
A . 3
B . 6
C . 9
D . 12
如图,AC、BD为⊙O的直径,且AC⊥BD,P、Q分别为半径OB、OA(不与端点重合)上的动点,直线PQ交⊙O于M、N.

-
(1) 比较大小:cos∠OPQsin∠OQP;
-
(2) 请你判断
 与OP·cos∠OPQ之间的数量关系,并给出证明;
与OP·cos∠OPQ之间的数量关系,并给出证明;
-
(3) 当∠APO=60°时,设MQ=m·MP,NQ=n·NP.
①求m+n的值;
②以OD为边在OD上方构造矩形ODKS,已知OD=1,OS=
 , 在Q点的移动过程中,
, 在Q点的移动过程中, 恒为非负数,请直接写出实数c的最大值.
恒为非负数,请直接写出实数c的最大值.
如图,在Rt△ABC中,AC=8,BC=6,直线l经过C,且l∥AB,P为l上一个动点,若△ABC与△PAC相似,则PC=

小明在学校阅览室看到如图1所示的一个报刊支架, 图2为它的侧面示意图, 已知AB=BC=BD=60 cm,∠CBD=40°.

-
(1) 如图2, 挂在B处报纸的垂落长度是50 cm, 为了摆放的整齐和美观, 要求报纸与地面的距离至少为10 cm,通过计算说明该报纸挂在B点处是否合理?
-
(2) 如图3,小明站在报刊支架前的点H处观察报刊支架(点D、C、H在同一水平线上),测得CH=99 cm,小明的眼睛到地面的高度GH为160 cm,当小明的视线恰好落在点B处时,求∠G的度数.(结果精确到0.1 cm.参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364, sin40°≈ 0.643, cos40°≈0.766,tan40°≈0.839, sin49°≈0.755,cos49°≈0.656,tan49°≈1.150.)
小红将笔记本电脑水平放置在桌子上,当显示屏  与底板
与底板  所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图如图2.使用时为了散热,她在底板下垫入散热架
所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图如图2.使用时为了散热,她在底板下垫入散热架  后,电脑转到
后,电脑转到  位置(如图3),侧面示意图为图4.已知
位置(如图3),侧面示意图为图4.已知  ,
,  于点
于点  ,
,  .
.
 与底板
与底板  所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图如图2.使用时为了散热,她在底板下垫入散热架
所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图如图2.使用时为了散热,她在底板下垫入散热架  后,电脑转到
后,电脑转到  位置(如图3),侧面示意图为图4.已知
位置(如图3),侧面示意图为图4.已知  ,
,  于点
于点  ,
,  .
. 
-
(1) 求
 的度数.
的度数.
-
(2) 显示屏的顶部
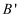 比原来的顶部
比原来的顶部  升高了多少?
升高了多少?
-
(3) 如图4,垫入散热架后,要使显示屏
 与水平线的夹角仍保持120°,则显示屏
与水平线的夹角仍保持120°,则显示屏  应绕点
应绕点  '按顺时针方向旋转多少度?并说明理由.
'按顺时针方向旋转多少度?并说明理由.
在墙角用若干个边长为1cm的小正方体摆成如图所示的几何体,则此几何体的体积为cm3 .

在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.

-
(1) 填空:∠ABC=°,△ABC的面积为.
-
(2) 判断△ABC与△DEF是否相似,并说明理由.
-
(3) 请在图中再画一个和△ABC相似但相似比不为1的格点三角形.
锐角  中,BC=6,
中,BC=6,  的面积为12,两动点M,N分别在边AB,AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与
的面积为12,两动点M,N分别在边AB,AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与  公共部分的面积为y(y>0).
公共部分的面积为y(y>0).
 中,BC=6,
中,BC=6,  的面积为12,两动点M,N分别在边AB,AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与
的面积为12,两动点M,N分别在边AB,AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与  公共部分的面积为y(y>0).
公共部分的面积为y(y>0). 
-
(1)
 中,边BC上高AD=;
中,边BC上高AD=;
-
(2) 若PQ恰好落在边BC上时如(图1),求x的值;
-
(3) 当PQ在
 外部时如(图2),求y关于x的函数关系式(写出x的范围).
外部时如(图2),求y关于x的函数关系式(写出x的范围).
如图,点O是△ABC的边AB上一点,⊙O与边AC相切于点E,与边BC,AB分别相交于点D,F,且DE=EF.

-
(1) 求证:∠C=90°;
-
(2) 当BC=3,sinA=
 时,求AF的长.
时,求AF的长.
如图,在等腰Rt△ABC中,∠ABC=90°,AB=2  ,点E为AC的中点,点D在CA的延长线上,∠BDA=30°,则CD的长是( )
,点E为AC的中点,点D在CA的延长线上,∠BDA=30°,则CD的长是( )
 ,点E为AC的中点,点D在CA的延长线上,∠BDA=30°,则CD的长是( )
,点E为AC的中点,点D在CA的延长线上,∠BDA=30°,则CD的长是( ) 
A . 2  +2
B . 4
+2
B . 4  ﹣2
C . 4
﹣2
C . 4  +2
D . 4
+2
D . 4  +4
+4
 +2
B . 4
+2
B . 4  ﹣2
C . 4
﹣2
C . 4  +2
D . 4
+2
D . 4  +4
+4
如图,有几个小正方体组成的;立体图形的主视图是( )


A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
最近更新
- 下图为南半球某地海平面等压线图,P点吹北风,则下列叙述正确的是 ①近地面气温,甲地气温低,乙地气温高②甲地可能为云
- 世界上第一次把圆周率的数值计算到小数点后第七位数字的数学家是A.张衡B.祖冲之C.蔡伦D.贾思勰
- 有关催化剂的说法错误的是( ) A.反应前后本身质量不变 B.反应前后化学性质不变C.一定加快化学反应速率
- 过⊙O内一点M的最长弦为10 cm,最短弦长为8cm,则OM的长为( ) A.9cm B.6cm
- 同志曾对一个外国来访同志说过:“……哎!1927年,老蒋够厉害啦!他把我们像鸡蛋一样地摔在地上。可他没想到,当时国外的许
- 人体血糖浓度的相对稳定受多种因素影响。现有甲、乙、丙三人,甲正常,乙的胰岛B细胞被自身免疫反应所破坏,丙的胰岛B细胞功能
- 不等式2x+3≥5的解集在数轴上表示正确的是( )
- 人体稳态的调节能力是有一定限度的。下列现象属于内环境稳态失调的是 A. 寒冷时出现寒颤
- (08年西工大附中文)设函数,其中(Ⅰ)若f(x)在x=3处取得极值,求常数a 的值;(Ⅱ)若f(x)在上为增函数,求a
- 外来物种越来越多,让人欢喜让人忧,如美国白蛾,对树木造成极大危害,试回答: (1)白蛾的幼虫喜食桑叶,与家蚕构成了___
- – Have you _____ some new idea ? -- Yeah. I’ll tell you la
- We all know that, __________, the situation will get worse.A
- 商场搬运工要把一箱苹果沿倾角为θ的光滑斜面推上水平台,如图4所示,他由斜面低端以初速度vo开始将箱推出(箱与手分离),这
- 阅读新闻,根据要求完成题目。(6分) 2014年3月1日晚9时许,云南昆明火车站发生一起严重暴力恐怖袭击事件,新疆分裂势
- 如图,双曲线y=-(x<0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴负半轴的夹角,AB∥x轴
- 化简 ▲ .的平方根为 ▲ 。
- As teenagers,you have many dreams.These dreams can be very b
- 一宇宙飞船绕地心做半径为r的匀速圆周运动,飞船舱内有一质量为m的人站在可称体重的台秤上.用R表示地球的半径,g表示地球表
- --- How do you feel about taking the job in Los Angeles? --
- 设 当时,取得最大值,则( ) A、一定是偶函数 B、一定



