九年级(初三)数学下学期下册试题
如图是由几个相同的小正方体搭成的几何体的三视图,则搭成这个几何体的小正方体的个数是( )


A . 4个
B . 5个
C . 6个
D . 7个
如图,已知点A(-1,0)和点B(1,2),在坐标轴上确定点P,使△ABP为直角三角形,则满足条件的点P共有 ( )
A . 2个
B . 3个
C . 6个
D . 7个
如图,已知△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,已知AC=3,BC=4.

-
(1) 线段AD,CD,CD,BD是不是成比例线段?写出你的理由;
-
(2) 在这个图形中,能否再找出其他成比例的四条线段?如果能,请至少写出两组.
如图1,△ABC中,∠B=30°,点D在BA的延长线上,点E在BC边上,连接DE,交AC于点F.若∠EFC=60°,DE=2AC,求  的值.某学习小组的同学经过思考,交流了自己的想法:
的值.某学习小组的同学经过思考,交流了自己的想法:
 的值.某学习小组的同学经过思考,交流了自己的想法:
的值.某学习小组的同学经过思考,交流了自己的想法: 小明:“通过观察和度量,发现∠C与∠D存在某种数量关系”;
小强:“通过构造三角形,证明三角形相似,进而可以求得  的值.
的值.
老师:如图2,将原题中“点D在BA的延长线上,点E在BC边上”改为“点D在AB边上,点E在BC的延长线上”,添加条件“BC=5  ,EC=4
,EC=4  ”,其它条件不变,可求出△BED的面积.
”,其它条件不变,可求出△BED的面积.

请回答:
-
(1) 用等式表示∠C、∠D的数量关系并证明;
-
(2) 求
 的值;
的值;
-
(3) △BDE的面积为(直接写出答案).
sin30°的值为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知在Rt△ABC中,∠C=90°, , BC=3,那么AC= .
, BC=3,那么AC= .
 , BC=3,那么AC= .
, BC=3,那么AC= .
如图是一个几何体的三种视图,则这个几何体是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .
如图是6月12日至25日期间全国新冠肺炎新增确诊病例统计图,根据图中信息,下列描述不正确的是( )

A . 13日新增确诊病例数最多
B . 21日新增确诊病例数与24日相同
C . 新增确诊病例数最少出现在12日
D . 13日后新增确诊病例数持续下降
“雪龙”号考察船在某海域进行科考活动,在点A处测得小岛C在它的东北方向上,它沿南偏东37°方向航行2海里到达点B处,又测得小岛C在它的北偏东23°方向上(如图所示),求“雪龙”号考察船在点B处与小岛C之间的距离.
(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,  ≈1.4,
≈1.4,  ≈1.7)
≈1.7)

如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.

-
(1) 求∠BPQ的度数;
-
(2) 求该电线杆PQ的高度(结果精确到1m).
备用数据:
 ,
,  .
.
如果反比例函数的图象经过点(-3,-4),那么函数的图象在第象限.
将如图所示表面带有图案的正方体沿某些棱展开后,得到的图形是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在  中,
中,  ,
,  轴,点A在反比例函数
轴,点A在反比例函数 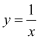 的图象上.若点B在y反比例函数
的图象上.若点B在y反比例函数  的图象上,则k的值为( )
的图象上,则k的值为( )
 中,
中,  ,
,  轴,点A在反比例函数
轴,点A在反比例函数 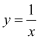 的图象上.若点B在y反比例函数
的图象上.若点B在y反比例函数  的图象上,则k的值为( )
的图象上,则k的值为( ) 
A .  B .
B .  C . 3
D . -3
C . 3
D . -3
 B .
B .  C . 3
D . -3
C . 3
D . -3
近年来,有私家车的业主越来越多,某小区为解决“停车难”问题,拟建造一个地下停车库.如图是该地下停车库坡道入口的设计示意图,其中水平线AB=10m,BD⊥AB,∠BAD=20°,点C在BD上,BC=1m.根据规定,地下停车库坡道入口上方要张贴限高标志,以提醒驾驶员所驾车辆能否安全驶入.李建认为CD的长度就是限制的高度,而孙杰认为应该以CE的长度作为限制的高度.李建和孙杰谁说的对?请你判断并计算出限制高度.(结果精确到0.1m,参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)

如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点 A 在反比例函数 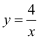 (x>0)的图象上,则经过点 B 的反比例函数解式为.
(x>0)的图象上,则经过点 B 的反比例函数解式为.
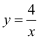 (x>0)的图象上,则经过点 B 的反比例函数解式为.
(x>0)的图象上,则经过点 B 的反比例函数解式为. 
如图放置的几何体的左视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知圆锥的底面半径为1cm,母线长为3cm,则其侧面积为( ) 

A . π
B . 2π
C . 3π
D . 4π
如图,面积为5的四边形ABCD与四边形A1B1C1D1是以坐标原点O为位似中心的位似图形,对应点A、A1的坐标分别是(2,2)、(4,4),则四边形A1B1C1D1的面积为.

如图,点A为反比例函数  的图象上一点,过A作AB⊥x轴于点B , 连接OA , 已知△ABO的面积为3,则k值为( ).
的图象上一点,过A作AB⊥x轴于点B , 连接OA , 已知△ABO的面积为3,则k值为( ).
 的图象上一点,过A作AB⊥x轴于点B , 连接OA , 已知△ABO的面积为3,则k值为( ).
的图象上一点,过A作AB⊥x轴于点B , 连接OA , 已知△ABO的面积为3,则k值为( ). 
A . -3
B . 3
C . -6
D . 6
如图,直线y= 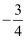 x+6与x轴交于点A,与y轴交于点B,点P在线段OA上运动(点P与点A不重合,且PA≤
x+6与x轴交于点A,与y轴交于点B,点P在线段OA上运动(点P与点A不重合,且PA≤ 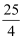 )。以P为圆心,PA为半径作⊙P交线段AB于另一点C,过点C作⊙P的切线交y轴于点D。
)。以P为圆心,PA为半径作⊙P交线段AB于另一点C,过点C作⊙P的切线交y轴于点D。
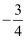 x+6与x轴交于点A,与y轴交于点B,点P在线段OA上运动(点P与点A不重合,且PA≤
x+6与x轴交于点A,与y轴交于点B,点P在线段OA上运动(点P与点A不重合,且PA≤ 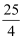 )。以P为圆心,PA为半径作⊙P交线段AB于另一点C,过点C作⊙P的切线交y轴于点D。
)。以P为圆心,PA为半径作⊙P交线段AB于另一点C,过点C作⊙P的切线交y轴于点D。 
-
(1) 求线段AB的长;
-
(2) 求证:DB=DC;
-
(3) 设点P(x,0),线段BD的长为y。
①求y关于x的函数关系式;
②当BD·AC的值最大时,求点D的坐标。
最近更新
- 如图所示某生态系统的食物网,下列有关叙述正确的是( )A.该食物网中的食物链,是通过捕食或竞争的关系形成的 B.该食
- 下列客观事实的微观解释正确的是( )选项客观事实微观解释A 品红在热水中扩散比在冷水中快水分子间存在间隙BH2O 在
- 已知:△ABC中,AB=,tanB=,sinC= 求BC的长.
- 青石棉(cricidolite)是世界卫生组织确认的一种致癌物质,是《鹿特丹公约》中受限制的46种化学品之一,青石棉的化
- 商代甲骨文中黍字出现300多次,稷字出现40次;周代《诗经》中提到谷物最多的也是黍和稷,分别达到28次和10次。由此,可
- 古代的“药金”外观与金相似,常被误以为是金子,冶炼方法如下,将碳酸锌、赤铜(Cu2O)、木炭按一定比例混合,加热到800
- 蚕妇吟 (南宋)谢枋得 子规啼彻四更时,起视蚕稠怕叶稀。 不信楼头杨柳月,玉人①歌舞未曾归。 【注】①玉人:美人
- ---Turn off the light. --- ? ---I asked you to tur
- 如图所示,两个物体A、B的质量均为1kg,各接触面之间的动摩擦因数均为0.3,同时有F=1N的两个水平力分别作用在A、B
- ......
- 阅读下面语段,完成小题。(7分)人生在世,有些事是应该在乎的,比如我们的人格、我们的尊严、做人的道德操守、人生价值取向等
- 一束光线照射到平面镜上,当反射光线与入射光线的夹角为140°°时,反射角等于 °,入射光线与镜面的夹角等于
- 《全球通史》中描述:“新皇帝废除此前的王国和诸侯,将广阔的国土划分为若干行政区,每一行政区都配备一批由中央政府任命,并向
- 下列加点词语使用不正确的一项是( )(2分) A.同学们或戏水玩沙,或放风筝,尽情享受天伦之乐。 B.如果不采取有力
- 请观察下面两幅图,回答问题下列有关旅游活动增多对环境的影响说法正确的是() ①对动植物的破坏 ②有利于背景环境的保护
- 我国最大的湖泊和最大的淡水湖分别是( ) A.鄱阳湖、洞庭湖 B.青海湖、洞庭湖 C.鄱阳湖、太湖D.青海湖、
- 下列四幅图片中,能够反映热带草原景观的是()
- 下列各项可存在等位基因的是() A.四分体 B.一个双链DNA分子 C.染色体组 D.非同源染
- .Our neighbor has ______ ours. A.as a big house as
- 物理学的发展极大地丰富了人类对物质世界的认识,推动了科学技术的创新和革命,促进了物质生产的繁荣与人类文明的进步。关于物理



