九年级(初三)数学下学期下册试题
反比例函数y=  的图象在每一象限内,y随x的增大而减小,则k的取值范围是( )
的图象在每一象限内,y随x的增大而减小,则k的取值范围是( )
 的图象在每一象限内,y随x的增大而减小,则k的取值范围是( )
的图象在每一象限内,y随x的增大而减小,则k的取值范围是( )
A . k  1
B . k
1
B . k 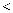 1
C . k=1
D . k≠1
1
C . k=1
D . k≠1
 1
B . k
1
B . k 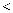 1
C . k=1
D . k≠1
1
C . k=1
D . k≠1
如图,已知△ABC,D、E分别在边AB、AC上,下列条件中,不能确定△ADE∽△ACB的是( )

A . ∠AED=∠B
B . ∠BDE+∠C=180°
C . AD•BC=AC•DE
D . AD•AB=AE•AC
如图,在平面直角坐标系中,等腰直角三角形ABC的顶点A,B分别在x轴、y轴的正半轴上,∠ABC=90°,CA⊥x轴,点C在函数y=  (x>0)的图象上,若AB=2,则k的值为( )
(x>0)的图象上,若AB=2,则k的值为( )
 (x>0)的图象上,若AB=2,则k的值为( )
(x>0)的图象上,若AB=2,则k的值为( )
A . 4
B . 2  C . 2
D .
C . 2
D . 
 C . 2
D .
C . 2
D . 
如图,已知反比例函数  (k≠0)的图象过点A(﹣3,2).
(k≠0)的图象过点A(﹣3,2).

-
(1) 求这个反比例函数的解析式;
-
(2) 若B(x1 , y1),C(x2 , y2),D(x3 , y3)是这个反比例函数图象上的三个点,若x1>x2>0>x3 , 请比较y1 , y2 , y3的大小,并说明理由.
若两个相似三角形的面积之比为1:4,则它们的周长之比为( )
A . 1:2
B . 2:1
C . 1:4
D . 4:1
如图,已知  …
…  是
是  轴上的点,且
轴上的点,且  …
…  ,分别过点
,分别过点  …
…  作
作  轴的垂线交反比例函数
轴的垂线交反比例函数  的图象于点
的图象于点  …
…  ,过点
,过点  作
作  于点
于点  ,过点
,过点  作
作  于点
于点  ……记
……记  的面积为
的面积为 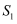 ,
,  的面积为
的面积为  ……
……  的面积为
的面积为  ,则
,则  …
…  等于.
等于.
 …
…  是
是  轴上的点,且
轴上的点,且  …
…  ,分别过点
,分别过点  …
…  作
作  轴的垂线交反比例函数
轴的垂线交反比例函数  的图象于点
的图象于点  …
…  ,过点
,过点  作
作  于点
于点  ,过点
,过点  作
作  于点
于点  ……记
……记  的面积为
的面积为 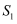 ,
,  的面积为
的面积为  ……
……  的面积为
的面积为  ,则
,则  …
…  等于.
等于. 
如图1,抛物线C1:y=x2+ax与C2:y=﹣x2+bx相交于点O、C,C1与C2分别交x轴于点B,A,且B为线段AO的中点.

-
(1) 求
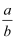 的值;
的值;
-
(2) 若OC⊥AC,求△OAC的面积;
-
(3) 抛物线C2的对称轴为l,顶点为M,在(2)的条件下:
①点P为抛物线C2对称轴l上一动点,当△PAC的周长最小时,求点P的坐标;
②如图2,点E在抛物线C2上点O与点M之间运动,四边形OBCE的面积是否存在最大值?若存在,求出面积的最大值和点E的坐标;若不存在,请说明理由.
若点A(1,-2)、B(-2,a)在同一个反比例函数的图象上,则a的值为.
如图,零件的外径为16cm, 要求它的壁厚x, 需要先求出内径AB, 现用一个交叉钳(AD与BC相等)去量,若测得OA:OD=OB:OC=3:1,CD=5cm,你能求零件的壁厚x吗?

如图,在直角坐标系中,△ABC的各顶点坐标为A(﹣1,1),B(2,3),C(0,3).现以坐标原点为位似中心,作△A′B′C′,使△A′B′C′与△ABC的位似比为 . 则点A的对应点A′的坐标为
. 则点A的对应点A′的坐标为
 . 则点A的对应点A′的坐标为
. 则点A的对应点A′的坐标为 
如图,在△ABC中,DE∥BC,DB=2AD,△ADE的面积为1,则四边形DBCE的面积为( )

A . 3
B . 5
C . 6
D . 8
如图,斜坡  长
长  米,坡度
米,坡度  ︰
︰  ,
,  ,现计划在斜坡中点
,现计划在斜坡中点  处挖去部分坡体修建一个平行于水平线
处挖去部分坡体修建一个平行于水平线  的平台
的平台  和一条新的斜坡
和一条新的斜坡  .
.
 长
长  米,坡度
米,坡度  ︰
︰  ,
,  ,现计划在斜坡中点
,现计划在斜坡中点  处挖去部分坡体修建一个平行于水平线
处挖去部分坡体修建一个平行于水平线  的平台
的平台  和一条新的斜坡
和一条新的斜坡  .
.
-
(1) 若修建的斜坡
 的坡角为
的坡角为  ,求平台
,求平台  的长;(结果保留根号)
的长;(结果保留根号)
-
(2) 斜坡
 正前方一座建筑物
正前方一座建筑物  上悬挂了一幅巨型广告
上悬挂了一幅巨型广告  ,小明在
,小明在  点测得广,
点测得广,  告顶部
告顶部  的仰角为
的仰角为  ,他沿坡面
,他沿坡面 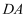 走到坡脚
走到坡脚  处,然后向大楼方向继行走
处,然后向大楼方向继行走  米来到
米来到  处,测得广告底部
处,测得广告底部  的仰角为
的仰角为 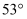 ,此时小明距大楼底端
,此时小明距大楼底端  处
处 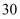 米.已知
米.已知  、
、  、
、  、
、  、
、  在同一平面内,
在同一平面内,  、
、  、
、  、
、  在同一条直线上,求广告
在同一条直线上,求广告  的长度.(参考数据:
的长度.(参考数据:  ,
,  ,
,  ,
,  ,
,  )
)
如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点O)20米的A处,则小明的影子AM长为米.

如图,吊车在水平地面上吊起货物时,吊绳BC与地面保持垂直,吊臂AB与水平线的夹角为64°,吊臂底部A距地面1.5m.(计算结果精确到0.1m,参考数据sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)

-
(1) 当吊臂底部A与货物的水平距离AC为5m时,吊臂AB的长为m.
-
(2) 如果该吊车吊臂的最大长度AD为20m,那么从地面上吊起货物的最大高度是多少?(吊钩的长度与货物的高度忽略不计)
为了解决楼房之间的采光问题,有关部门规定两幢楼房之间的最小距离要使中午12时不能遮光  如图,旧楼的一楼窗台高1m,现计划在旧楼正南方20m处建一幢新楼
如图,旧楼的一楼窗台高1m,现计划在旧楼正南方20m处建一幢新楼  已知新昌冬天中午12时太阳从正南方照射的光线与水平线的夹角最小为
已知新昌冬天中午12时太阳从正南方照射的光线与水平线的夹角最小为  ,问新楼房最高可建多少米?
,问新楼房最高可建多少米?  结果精确到
结果精确到  ,
,  .
.
 如图,旧楼的一楼窗台高1m,现计划在旧楼正南方20m处建一幢新楼
如图,旧楼的一楼窗台高1m,现计划在旧楼正南方20m处建一幢新楼  已知新昌冬天中午12时太阳从正南方照射的光线与水平线的夹角最小为
已知新昌冬天中午12时太阳从正南方照射的光线与水平线的夹角最小为  ,问新楼房最高可建多少米?
,问新楼房最高可建多少米?  结果精确到
结果精确到  ,
,  .
. 
点 ,
,  ,
,  在反比例函数
在反比例函数 的图象上,则
的图象上,则 ,
,  ,
,  的大小关系是( )
的大小关系是( )
 ,
,  ,
,  在反比例函数
在反比例函数 的图象上,则
的图象上,则 ,
,  ,
,  的大小关系是( )
的大小关系是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
小洋用一张半径为24cm的扇形纸板做一个如图所示的圆锥形小丑帽子侧面(接缝忽略不计),如果做成的圆锥形小丑帽子的底面半径为10cm,那么这张扇形纸板的面积是( )

A . 120πcm2
B . 240πcm2
C . 260πcm2
D . 480πcm2
一个圆柱的侧面展开图是长方形,这个长方形的一组邻边长分别是6和8,则这个圆柱的底面半径是( )
A . 3
B .  C .
C .  D .
D .  或
或 
 C .
C .  D .
D .  或
或 
耸立在临清市城北大运河东岸的舍利宝塔,是“运河四大名塔”之一(如图1).数学兴趣小组的小亮同学在塔上观景点P处,利用测角仪测得运河两岸上的A,B两点的俯角分别为17.9°,22°,并测得塔底点C到点B的距离为142米(A、B、C在同一直线上,如图2),求运河两岸上的A、B两点的距离(精确到1米).
(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin17.9°≈0.31,cos17.9°≈0.95,tan17.9°≈0.32) 
如图,函数y=  和y=﹣
和y=﹣  的图象分别是l1和l2 . 设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则△PAB的面积为.
的图象分别是l1和l2 . 设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则△PAB的面积为.
 和y=﹣
和y=﹣  的图象分别是l1和l2 . 设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则△PAB的面积为.
的图象分别是l1和l2 . 设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则△PAB的面积为. 
最近更新
- 如图所示,某同学在地面上拉着一个质量为m=30kg的箱子匀速前进,已知箱与地面间的动摩擦因数为μ=0.5,拉力F1与水平
- 男性主要的性器官是( )A.睾丸B.附睾C.输精管D.前列腺
- 阅读下面文字,完成文后的题目 顽童的成长 1939年,费因曼进入普林斯顿大学高等研究院深造。麻省理工是一所完全美国化的学
- 我国婚姻法规定禁止近亲结婚的理论依据是( )A、近亲婚配的家庭不稳定 B、近亲婚配其后代必患
- 如图所示,水平放置的平行金属板的B板接地,A、B两板间的电势差为+U,两板间为匀强电场,间距为d。在两板之间有一长为l的
- GIS中,不同类型的地理空间信息储存存在不同的“圈层”中,重叠不同的“圈层”要素,就形成不同主题的地图,可以分析不同要素
- 关于光电效应,下列说法中正确的是( )A.光电子的最大初动能随着入射光的强度增大而增大B.只要入射光的强度足够强,
- 2009年9月2同,国家决定在公共卫生与基层医疗卫生事业单位和其他事业单位实施绩效工资。对事业单位实施绩效工资
- 下列词语中,字形和加点字的读音全都正确的一项是 ( ) A.指摘 沤心沥血
- 质量为ag的铜丝,在空气中灼热变黑,趁热放入下列物质中,铜丝变红,质量仍为ag的是 ( )
- 冬天同学们课间要去室外换气,当步入寒冷的室外环境时,机体最可能发生的是 A.分泌甲状腺激素减少 B.皮肤
- His _____ expression suggests that the news he read just no
- 19世纪末20世纪初垄断组织出现 ① 阻碍了生产力的发展 ② 顺应了生产力的发展
- 计算(xy3)2的结果是( ▲ )A.xy6 B.x2y3
- “大义当前,不容反顾,只求于救亡主张贯彻,有济于国家,为功为罪,一听国人处置。”这表明张学良、扬虎城发动西安事变是为了
- 阅读下面一段文字,根据要求写一篇不少于800字的作文。刘翔在雅典奥运会上夺得110米栏冠军之后,人们惊喜地发现,“飞人”
- 如图9所示,空间有一垂直纸面向外的磁感应强度为0.5T的匀强磁场,一质量为0.2kg且足够长的绝缘塑料板静止在光滑水平面
- 可逆反应达到平衡的重要特征是:A.反应停止了 B.正、逆反应的速度
- “金无足赤,人无完人”对于自己的错误,正确的做法是 ①后果轻可以承担,后果严重就应考虑 ②认真承认错误,并可以找理由推卸
- 已知某种限制性内切酶在一线性DNA分子上有3个酶切位点,如图中箭头所指。如果该线性 DNA分子在3个酶切位点上都被该酶切



