九年级(初三)数学下学期下册试题
如图,在四个小正方体搭成的几何体中,每个小正方体的棱长都是1,则该几何体的三视图的面积之和是.

如图,△ADE∽△ABC,AD=3cm,AE=2cm,CE=4cm,BC=9cm

-
(1) 求BD、DE的长;
-
(2) 求△ADE与△ABC的周长比.
有五张正面分别写有数字﹣4,﹣3,0,2,3的卡片,五张卡片除了数字不同外其余全部相同,现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为n,则抽取的n既能使关于x的方程(n+3)x2+(n+1)x+  =0有实数根,又能使以x为自变量的反比例函数y=
=0有实数根,又能使以x为自变量的反比例函数y=  的图象在每个象限内y随x的增大而增大的概率为.
的图象在每个象限内y随x的增大而增大的概率为.
 =0有实数根,又能使以x为自变量的反比例函数y=
=0有实数根,又能使以x为自变量的反比例函数y=  的图象在每个象限内y随x的增大而增大的概率为.
的图象在每个象限内y随x的增大而增大的概率为.
先化简,再求代数式  的值,其中
的值,其中  =tan60°.
=tan60°.
 的值,其中
的值,其中  =tan60°.
=tan60°.
如图,在亚丁湾一海域执行护航任务的我海军某军舰由东向西行驶.在航行到B处时,发现灯塔A在我军舰的正北方向500米处;当该军舰从B处向正西方向行驶至达C处时,发现灯塔A在我军舰的北偏东60°的方向.求该军舰行驶的路程.(计算过程和结果均不取近似值)

若干盒奶粉放在桌子上,如图是一盒奶粉的实物以及这若干盒奶粉所组成的几何体从正面、左面、上面所看到的图形,则这些奶粉共有( )盒.

A . 3
B . 4
C . 5
D . 不能确定
如图所示的几何体的俯视图是 ( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  D .
D . 
计算:(3.14﹣π)0﹣ ﹣|﹣3|+4sin60°
﹣|﹣3|+4sin60°
 ﹣|﹣3|+4sin60°
﹣|﹣3|+4sin60°
燃灯佛舍利塔(简称燃灯塔)是通灯塔的高度.他先测量出燃灯塔落在地面上的影长为12米,然后在同一时刻立一根高2米的标杆,测得标杆影长为0.5米,那么燃灯塔高度为米.

网格中每个小正方形的边长都是1.

-
(1) 将图①中的格点三角形ABC平移,使点A平移至点A`,画出平移后的三角形;
-
(2) 在图②中画一个格点三角形DEF,使△DEF∽△ABC,且相似比为2∶1;
-
(3) 在图③中画一个格点三角形PQR,使△PQR∽△ABC,且相似比为
 ∶1.
∶1.
如图所示为一无盖长方体盒子的展开图(重叠部分不计),可知该无盖长方体的容积为( )

A . 4
B . 6
C . 8
D . 12
如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(1,2),B(7,2),C(5,6).

-
(1) 请以图中的格点为顶点画出一个△A1B1C , 使得△A1B1C ∽△ABC , 且△A1B1C与△ABC的周长比为1:2;(每个小正方形的顶点为格点)
-
(2) 根据你所画的图形,直接写出顶点A1和B1的坐标.
如图,已知点A在反比例函数y= (x<0)上,B,C两点在x轴上,△ABC是以AC为底边的等腰直角三角形,过点B作BD⊥AC交y轴于点E,交AC于点D,若△BCE的面积为3,则k的值为.
(x<0)上,B,C两点在x轴上,△ABC是以AC为底边的等腰直角三角形,过点B作BD⊥AC交y轴于点E,交AC于点D,若△BCE的面积为3,则k的值为.
 (x<0)上,B,C两点在x轴上,△ABC是以AC为底边的等腰直角三角形,过点B作BD⊥AC交y轴于点E,交AC于点D,若△BCE的面积为3,则k的值为.
(x<0)上,B,C两点在x轴上,△ABC是以AC为底边的等腰直角三角形,过点B作BD⊥AC交y轴于点E,交AC于点D,若△BCE的面积为3,则k的值为.
若点A(-4,y1)、B(-2,y2)、C(2,y3)都在反比例函数  的图像上,则y1、y2、y3的大小关系是( )
的图像上,则y1、y2、y3的大小关系是( )
 的图像上,则y1、y2、y3的大小关系是( )
的图像上,则y1、y2、y3的大小关系是( )
A . y1>y2>y3
B . y3>y2>y1
C . y2>y1>y3
D . y1>y3>y2
已知反比例函数  ,当自变量
,当自变量  的值从3增加到6时,函数值减少了1,则函数的表达式为( )
的值从3增加到6时,函数值减少了1,则函数的表达式为( )
 ,当自变量
,当自变量  的值从3增加到6时,函数值减少了1,则函数的表达式为( )
的值从3增加到6时,函数值减少了1,则函数的表达式为( )
A .  B .
B .  C .
C . 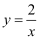 D .
D . 
 B .
B .  C .
C . 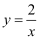 D .
D . 
2013年9月23日强台风“天兔”登录深圳,伴随着就是狂风暴雨梧桐山山坡上有一棵与水平面垂直的大树,台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示).已知山坡的坡角∠AEF=23°,量得树干的倾斜角为∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=3m.


-
(1) 求∠DAC的度数;
-
(2) 求这棵大树折断前的高度?(结果保留根号).
三角形面积是  ,底边为
,底边为  ,高是
,高是  ,则
,则  与
与  的关系式的图象位于象限.
的关系式的图象位于象限.
 ,底边为
,底边为  ,高是
,高是  ,则
,则  与
与  的关系式的图象位于象限.
的关系式的图象位于象限.
如图,在△ABC中,AB≠AC.D、E分别为边AB、AC上的点.AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件:,可以使得△FDB与△ADE相似.(只需写出一个)

如图是一个放置在水平桌面的锥形瓶,它的俯视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .
如图,已知在平面直角坐标系xOy中,抛物线y=  与y轴交于点A,顶点为B,直线l:y=-
与y轴交于点A,顶点为B,直线l:y=- 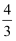 x+b经过点A,与抛物线的对称轴交于点C,点P是对称轴上的一个动点,若AP+
x+b经过点A,与抛物线的对称轴交于点C,点P是对称轴上的一个动点,若AP+ 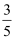 PC的值最小,则点P的坐标为( )
PC的值最小,则点P的坐标为( )
 与y轴交于点A,顶点为B,直线l:y=-
与y轴交于点A,顶点为B,直线l:y=- 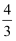 x+b经过点A,与抛物线的对称轴交于点C,点P是对称轴上的一个动点,若AP+
x+b经过点A,与抛物线的对称轴交于点C,点P是对称轴上的一个动点,若AP+ 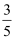 PC的值最小,则点P的坐标为( )
PC的值最小,则点P的坐标为( ) 
A . (3,1)
B . (3,  )
C . (3,
)
C . (3,  )
D . (3,
)
D . (3,  )
)
 )
C . (3,
)
C . (3,  )
D . (3,
)
D . (3,  )
)
最近更新
- 用电子式表示PH3分子与H+通过配位键形成的过程:______________________。由此可知,形成配位键的条
- 读下面两幅图,完成图后填空。(1)A、B、C三点都位于地球上五带中的____带,其中一年受太阳直射两次的是____点。
- 2008年5月12日,四川省发生8.0级地震,我校师生积极捐款,已知第一天捐款 4800元,第二天捐款6000元,第二天
- 下列有关细胞衰老和细胞凋亡的说法中,正确的是 A.衰老的生物体中,细胞都处于衰老状态 B.细胞凋亡是由细胞内的基因所决定
- 以诚待人,人人敬;以诚办事,事事成。失去了诚信,就等同于敌人毁灭了自己。播种诚信,你收获的就不仅仅是朋友的信任,还有可以
- 化学研究的核心内容是() A.物体的运动规律和光电现象 B.物质的组成、结构、性质和变化 C.生命有机体的形成及功能 D
- 诗歌承载着厚重的历史。下列诗句中,与红军长征途中发生在图3所示地点的相关历史事件是( ) A、金沙水拍云崖暖 B、大
- 8.下列有关文学常识的表述,不正确的一项是 A.韩愈,字退之,号昌黎,是唐代文学家、思想家,他和柳宗元等人发起并倡导了古
- It happened once, however, some seventy years ago, ______ th
- 如图是某森林生态系统物质和能量流向示意图,h、i、j、k表示不同用途的有机物(j是未利用部分),方框大小表示使用量。下列
- 关于细胞中的水分子的叙述,下列哪项有误 ( ) A.是以游离形式存在 B.是细胞中
- 课堂上老师做了一个实验:将液态空气倒入一只烧杯中,发现立即冒出大量气泡,把一根燃着的小木条置于烧杯口,小木条火焰熄灭;过
- 把文言文阅读材料中画横线的句子翻译成现代汉语。 (1)刘表雍容荆楚,坐观时变,自以为西伯可规。[来 (2)士之避乱荆州者
- 下列句子中成语使用不恰当的是( ) (2分)A.一到银泰百货和金华一百等商家打折的时候,商场里可谓人声鼎沸。B.洪
- 《大明律》与《秦律》相比,突出特点有
- 若分式的值为0,则x的值为 .
- 法国国旗从左自右的蓝、白、红三种颜色分别代表自由、平等、博爱。这源于 A.《权利法案》 B.《人权宣言》
- 读南亚地形分布图(图1)和该地区某城市的气候资料统计图(图2)。完成11--13题。 11.图2气候资料所示城市最可能是
- 1958年人民公社化运动具有很大的盲目性,主要是因为() A.当时我国的生产力还比较落后 B.“大跃进”运动已给国家造成
- 圆的内接正方形相对的两个顶点的坐标分别为 (I)求圆的方程 (II)若过点的直线与圆有且只有一个公共点,求直



