九年级(初三)数学下学期下册试题
计算:  .
.
 .
.
图1是一台用保护套套好的带键盘的平板电脑实物图,图2是它的示意图,忽略平板电脑的厚度,支架BE分别固定在平板电脑AD背面中点B处,桌面E处,EB可以绕点E转动,当点D在线段EF上滑动时,可调节平板电脑AD的倾斜角  ,经测量,
,经测量,  ,
,  ,支架
,支架  .(参考数据:
.(参考数据: 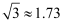 ,
,  ,
,  ,
,  ,结果保留一位小数)
,结果保留一位小数)
 ,经测量,
,经测量,  ,
,  ,支架
,支架  .(参考数据:
.(参考数据: 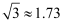 ,
,  ,
,  ,
,  ,结果保留一位小数)
,结果保留一位小数) 

-
(1) 连接AE,求证:
 ;
;
-
(2) 当
 时,求A,E两点间的距离;
时,求A,E两点间的距离;
-
(3) 当点D滑到距离F点1cm处时,视觉效果最好,求此时倾斜角
 的度数.
的度数.
已知反比例函数的图象经过点A(2,6).
-
(1) 求这个反比例函数的解析式;
-
(2) 这个函数的图象位于哪些象限?y随x的增大如何变化?
-
(3) 点B(3,4),C(5,2),D(
 ,
,  )是否在这个函数图象上?为什么?
)是否在这个函数图象上?为什么?
若反比例函数  的图像经过点
的图像经过点  ,则一次函数
,则一次函数  与
与  在同一平面直角坐标系中的大致图像是( )
在同一平面直角坐标系中的大致图像是( )
 的图像经过点
的图像经过点  ,则一次函数
,则一次函数  与
与  在同一平面直角坐标系中的大致图像是( )
在同一平面直角坐标系中的大致图像是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,原点O是△ABC和△A’B’C’的位似中心,点A(1,0)与点A’(-2,0)是对应点,△ABC的面积是  ,则△A’B’C’的面积是
,则△A’B’C’的面积是
 ,则△A’B’C’的面积是
,则△A’B’C’的面积是 
在如图所示的四个图形为两个圆或相似的正多边形,其中位似图形的个数为( )

A . 1个
B . 2个
C . 3个
D . 4个
圆锥的底面半径为5,侧面积为60π,则其侧面展开图的圆心角等于.
若反比例函数 的图象经过
的图象经过 , 则
, 则 的值是( )
的值是( )
 的图象经过
的图象经过 , 则
, 则 的值是( )
的值是( )
A . 2
B .  C . -2
D .
C . -2
D . 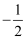
 C . -2
D .
C . -2
D . 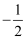
如图,线段AB两个端点的坐标分别为A(2,2)、B(3,1),以原点O为位似中心,在第一象限内将线段AB扩大为原来的2倍后得到线段CD,则端点C的坐标分别为( )

A . (4,4)
B . (3,3)
C . (3,1)
D . (4,1)
如图,抛物线  与x轴交于点A(-1,0),点B(3,0),与y轴正半轴交于点C.
与x轴交于点A(-1,0),点B(3,0),与y轴正半轴交于点C.
 与x轴交于点A(-1,0),点B(3,0),与y轴正半轴交于点C.
与x轴交于点A(-1,0),点B(3,0),与y轴正半轴交于点C.
-
(1) 抛物线的解析式为;
-
(2) P为抛物线上一点,连结AC,PC,若∠PCO=3∠ACO,点P的坐标为.
某校为检测师生体温,在校门安装了某型号测温门.如图为该测温门截面示意图,已知测温门AD的顶部A处距地面高为2.2m,为了解自己的有效测温区间.身高1.6m的小聪做了如下实验:当他在地面N处时测温门开始显示额头温度,此时在额头B处测得A的仰角为18°;在地面M处时,测温门停止显示额头温度,此时在额头C处测得A的仰角为60°求小聪在地面的有效测温区间MN的长度.(额头到地面的距离以身高计,计算精确到0.1m,sin18°≈0.31,cos18°≈0.95,tan18°≈0.32,  ≈1.73)
≈1.73)
 ≈1.73)
≈1.73)

如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=  (x<0)经过斜边OA上的点C,且OC:AC=1:2,与另一直角边交于点D,若S△OCD=12,则k=.
(x<0)经过斜边OA上的点C,且OC:AC=1:2,与另一直角边交于点D,若S△OCD=12,则k=.
 (x<0)经过斜边OA上的点C,且OC:AC=1:2,与另一直角边交于点D,若S△OCD=12,则k=.
(x<0)经过斜边OA上的点C,且OC:AC=1:2,与另一直角边交于点D,若S△OCD=12,则k=. 
计算:(﹣1)2+|  ﹣1|+2sin45°.
﹣1|+2sin45°.
 ﹣1|+2sin45°.
﹣1|+2sin45°.
已知如图:等边△ABC中,D是AB上一点,∠EDF=60o , 则tan∠AED=( )。
A . tan∠B
B . tan∠BFD
C . tan∠ADE
D . tan∠BDF
如图,五边形ABCDE是由五边形FGHMN经过位似变换得到的,点O是位似中心,F、G、H、M、N分别是OA、OB、OC、OD、OE的中点,则五边形ABCDE与五边形FGHMN的面积比是( )

A . 6:1
B . 5:1
C . 4:1
D . 2:1
如图,若要使图中的平面展开图折叠成正方形,相对面上两个数相等,则x-y=

如图,点A、B、C为正方形网格中的3个格点,则sin∠ACB=.

已知四条线段满足a=  ,将它改写成为比例式为(写出你认为正确的一个).
,将它改写成为比例式为(写出你认为正确的一个).
 ,将它改写成为比例式为(写出你认为正确的一个).
,将它改写成为比例式为(写出你认为正确的一个).
如果矩形的面积为6,那么它的长  与宽
与宽  的函数关系用图象表示为( )
的函数关系用图象表示为( )
 与宽
与宽  的函数关系用图象表示为( )
的函数关系用图象表示为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
-
(1) 计算:|﹣
 |﹣2cos60°+(1﹣
|﹣2cos60°+(1﹣  )0+(﹣1)2021.
)0+(﹣1)2021.
-
(2) 先化简,再求值:(
 )÷
)÷  ,其中x=
,其中x=  .
.
最近更新
- 按要求对下图中两极进行必要的联接并填空:(1)在A图中,使铜片上冒气泡。请加以必要联接,则联接后的装 置叫
- 函数f(x)=的零点个数为() A.0 B.1 C.2 D.3
- 设是夹角为的单位向量,若是单位向量,则的取值范围( ) A, B, C, D,
- Linda has two sisters. One is 11 and ______is 13. A.another
- 有人写诗描述19世纪八十年代初出现于上海的一种新事物:“东西遥隔语言通,此器名称德律风。沪上巨商装设广,几如面话一堂中。
- 在物理学的发展过程中,许多物理学家的科学发现推动了人类历史的进步。在对以下几位物理学家所作科学贡献的叙述中,正确的说法是
- 如图17-13所示,两个互相连接的金属环,粗环的电阻等于细环电阻的1/2,将细环套在变压器铁芯上时,A、B两点间电压为0
- 从 2008年9月1日 起,在全国统一停止征收个体工商户管理费和集市贸易市场管理费,工商部门不再直接参与市场建设。停止征
- (08浙江五校联考)韩国“首席科学家”黄禹锡曾因发表有关人类胚胎干细胞论文的造假行为,被处以最高处分――撤销教授职务。胚
- 阅读下面这首宋词,完成14-15题。 西江月① 【宋】苏轼 照野弥弥浅浪,横空隐隐层霄。障泥②未解玉骢骄,我欲醉眠芳草。
- 小敏想探究小球滚上斜面的最大高度与斜面倾角和小球质量的关系,将两个斜面AO与OB对接成如图装置,进行实验。①让质量为5克
- 在正三棱柱中,若,,则与所成角的大小为 A. 60° B. 90°
- 近代西方观察家曾将当时的一场战事称为“李鸿章一人与日本一国的战争”。其依据是A.鸦片战争后清政府对外来侵略已无力抵抗 B
- 文献纪录片《走近》中有这样一个情节:在西柏坡村的小院里,警卫员给梳头时拔下一根白发,毛打趣地说:“打了三个战役,白了一根
- 太原市公共自行车服务系统开通以来,单车日周转次数及服务半径居全国之首。市民办理租车卡后就可以在市区任意网点租用公共自行车
- A mom in Australia wastold by a doctor that her newborn son
- 氧化还原反应的实质是A.氧元素的得与失 B.化合价的升降C.电子的得失或
- 若NA表示阿伏加德罗常数的值,下列说法正确的是:( )A.在标准状况下,NA个水分子所占的体积约为22.4LB.
- 阅读材料,回答问题 材料一: 图一 攻占巴士底狱 图二 《人权宣言》 图三 处死路易十六
- (本小题满分12分) 如图,菱形的边长为,,.将菱形沿对角线折起,得到三棱锥,点是棱的中点,. (Ⅰ)求证:平面; (Ⅱ



