九年级(初三)数学下学期下册试题
在  中,
中,  ,
,  ,
,  ,点G是
,点G是  的重心,GH垂直于AB,垂足为H,则
的重心,GH垂直于AB,垂足为H,则  .
.
 中,
中,  ,
,  ,
,  ,点G是
,点G是  的重心,GH垂直于AB,垂足为H,则
的重心,GH垂直于AB,垂足为H,则  .
.
如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC,DE∥BC,那么在下列三角形中,与△EBD相似的三角形是( )

A . △ABC
B . △ADE
C . △DAB
D . △BDC
如图所示,一个几何体是由多个大小相同的小立方块搭成的,图中是从上面看到的图形,正方形中的数字表示在该位置小立方块的个数.请你画出从正面看和从左面看的这个几何体的形状图.

如图是一个由5个相同的正方体组成的立体图形,它的左视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,铜亭广场装有智能路灯,路灯设备由灯柱AC与支架BD共同组成(点C处装有安全监控,点D处装有照明灯),灯柱AC为6米,支架BD为2米,支点B到A的距离为4米,AC与地面垂直,∠CBD=60°.某一时刻,太阳光与地面的夹角为45°,求此刻路灯设备在地面上的影长为多少?

如图,在△ABC中,AB=AC=10cm,BC=16cm,DE=4cm.动线段DE(端点D从点B开始)沿BC边以1cm/s的速度向点C运动,当端点E到达点C时运动停止.过点E作EF∥AC交AB于点F(当点E与点C重合时,EF与CA重合),连接DF,设运动的时间为t秒(t≥0).

-
(1) 直接写出用含t的代数式表示线段BE、EF的长;
-
(2) 在这个运动过程中,△DEF能否为等腰三角形?若能,请求出t的值;若不能,请说明理由;
-
(3) 设M、N分别是DF、EF的中点,求整个运动过程中,MN所扫过的面积.
在比例尺为1:2000 的地图上测得 、
、 两地间的图上距离为
两地间的图上距离为 ,则
,则 两地间的实际距离为( )
两地间的实际距离为( )
 、
、 两地间的图上距离为
两地间的图上距离为 ,则
,则 两地间的实际距离为( )
两地间的实际距离为( )
A .  ;
B .
;
B .  ;
C .
;
C .  ;
D .
;
D .  .
.
 ;
B .
;
B .  ;
C .
;
C .  ;
D .
;
D .  .
.
如右图所示为我市某农村一古老的捣碎器,已知支撑柱AB的高为0.3米,踏板DE长为1.6米,支撑点A到踏脚D的距离为0.6米,现在踏脚着地,则捣头点E上升了( )米.

A . 0.6
B . 0.8
C . 1
D . 1.2
若反比例函数y= (k为常数,且k≠0)的图象过点(3,-4),则下列各点在该图象上的是 ( )
(k为常数,且k≠0)的图象过点(3,-4),则下列各点在该图象上的是 ( )
 (k为常数,且k≠0)的图象过点(3,-4),则下列各点在该图象上的是 ( )
(k为常数,且k≠0)的图象过点(3,-4),则下列各点在该图象上的是 ( )
A . (6,-8)
B . (-6,8)
C . (-3,4)
D . (-3,-4)
如图,上体育课,甲、乙两名同学分别站在C、D的位置时,乙的影子恰好在甲的影子里边,已知甲,乙同学相距1米.甲身高1.8米,乙身高1.5米,则甲的影长是多少米?

如图摆放的下列几何体中,左视图是圆的是( ).
A . 长方体  B . 圆柱体
B . 圆柱体  C . 圆锥体
C . 圆锥体  D . 球体
D . 球体 
 B . 圆柱体
B . 圆柱体  C . 圆锥体
C . 圆锥体  D . 球体
D . 球体 
小明身高为1.5m,某一时刻小明在阳光下的影子是0.5m;同一时刻同一地点,测得学校教学大楼的影长是5m,则该教学大楼的高度为( )
A . 12.5m
B . 15m
C . 20m
D . 25m
如图,强强同学为了测量学校一棵笔直的大树OE的高度,先在操场上点A处放一面平面镜,从点A处后退1m到点B处,恰好在平面镜中看到树的顶部E点的像;再将平面镜向后移动4m(即AC=4m)放在C处,从点C处向后退1.5m到点D处,恰好再次在平面镜中看到大树的顶部E点的像,测得强强的眼睛距地面的高度FB、GD为1.5m,已知点O,A,B,C,D在同一水平线上,且GD⊥OD,FB⊥OD,EO⊥OD.求大树OE的高度.(平面镜的大小忽略不计)

如图,已知直线  ,分别交直线m、n 于点 A、C、D、E、F,AB=5cm,AC=15cm,DE=3cm,则EF的长为cm.
,分别交直线m、n 于点 A、C、D、E、F,AB=5cm,AC=15cm,DE=3cm,则EF的长为cm.
 ,分别交直线m、n 于点 A、C、D、E、F,AB=5cm,AC=15cm,DE=3cm,则EF的长为cm.
,分别交直线m、n 于点 A、C、D、E、F,AB=5cm,AC=15cm,DE=3cm,则EF的长为cm.
如图1,在Rt△ABC中,∠C=90°,AC=3,BC=4,求作菱形DEFG,使点D在边AC上,点E、F在边AB上,点G在边BC上.小明发现所作的四边形DEFG是菱形,于是小明进一步探索,发现可作出的菱形的个数随着点D的位置变化而变化,当菱形的个数只有1个时CD的长的取值范围为.

如图,点A为反比例函数y=﹣  图象上一点,过A作AB⊥x轴于点B,连接OA,则△ABO的面积为( )
图象上一点,过A作AB⊥x轴于点B,连接OA,则△ABO的面积为( )
 图象上一点,过A作AB⊥x轴于点B,连接OA,则△ABO的面积为( )
图象上一点,过A作AB⊥x轴于点B,连接OA,则△ABO的面积为( ) 
A . 4
B . ﹣2
C . 2
D . 无法确定
如图是下列一个立体图形的三视图,则这个立体图形是( )
A . 圆锥
B . 球
C . 圆柱
D . 正方体
在平面直角坐标系中,点 , 直线
, 直线 轴.在矩形
轴.在矩形 中,
中, ,
,  .以点
.以点 在第一象限内直线
在第一象限内直线 上时为初始位置,将矩形
上时为初始位置,将矩形 以点
以点 为中心逆时针旋转,旋转角为
为中心逆时针旋转,旋转角为 .直线
.直线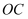 , 直线
, 直线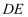 分别与直线
分别与直线 相交于点
相交于点 ,
,  .
.
 , 直线
, 直线 轴.在矩形
轴.在矩形 中,
中, ,
,  .以点
.以点 在第一象限内直线
在第一象限内直线 上时为初始位置,将矩形
上时为初始位置,将矩形 以点
以点 为中心逆时针旋转,旋转角为
为中心逆时针旋转,旋转角为 .直线
.直线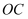 , 直线
, 直线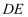 分别与直线
分别与直线 相交于点
相交于点 ,
,  .
.
-
(1) 如图1,当顶点
 落在直线
落在直线 上时(此时点
上时(此时点 与点
与点 重合).
重合).①求证:
 ;
;②求点
 的横坐标;
的横坐标; -
(2) 如图2,当顶点
 落在
落在 轴正半轴上时,请直接写出点
轴正半轴上时,请直接写出点 的横坐标;
的横坐标;
-
(3) 在矩形
 旋转过程中,当
旋转过程中,当 时,若
时,若 , 请直接写出此时点
, 请直接写出此时点 的横坐标.
的横坐标.
若点A(-2,3)在反比例函数y=  的图象上则k的值是( )
的图象上则k的值是( )
 的图象上则k的值是( )
的图象上则k的值是( )
A . -6
B . -1.5
C . 1.5
D . 6
如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,则楼房CD的高度为 m .( ≈1.7)
≈1.7)
 ≈1.7)
≈1.7)
最近更新
- 23.仿照下面的示例,自选话题,另写两个句子,要求运用比喻的修辞手法,句式与示例相同。(6分) 情意就像一座山,重要的不
- 下图反映的是中国古代哪一朝代的制度 A.秦朝 B.汉朝 C.唐朝
- 写出日常生活中常见的三种无机非金属材料________、________、__________。
- 若关于的分式方程无解,则 .
- 地球的平均半径是: ( ) A
- 以My hometown为题,写一篇80字左右的短文,要点如下:1.我的家乡是个美丽的小镇,离无锡不远。2.有许多名胜古
- 如图,已知二次函数的图像经过点A和点B.【小题1】求该二次函数的表达式【小题2】写出该抛物线的对称轴及顶点坐标;【小题3
- 将含有两对同源染色体,其DNA分子都已用32P标记的精原细胞,放在只含31P的原料中进行减数分裂。则该细胞所产生的四个精
- 若等腰梯形ABCD的上、下底之和为2,并且两条对角线所成的锐角为60°,则等腰梯形ABCD的面积为 。
- 下列属于特异性免疫的是()A. 泪液中的溶菌酶可杀死沙眼衣原体 B. 淋巴结内的吞噬细胞吞噬侵入人体的链球菌 C. 胃液
- 下列说法中正确的是 ▲ A、被活塞封闭在气缸中的一定质量的理想气体,若体积不变,压强增大,则气缸在单位面积上
- 在200米高的山顶上测得一建筑物顶部与底部的俯角分别为与,则建筑物高为 ( ) A.米
- p{font-size:10.5pt;line-height:150%;margin:0;padding:0;}td{f
- 1945年秋,在重庆将《沁园春·雪》赠与柳亚子,此次重庆之行 A.签署了《双十协定》
- 工业碳酸钠由于在生产过程中原料盐和工艺等的原因,常会含有Na2SO4 、NaCl中的一种或两种杂质。现有工业碳酸钠样品,
- 下图为某家庭农场示意图,据此回答1—2题。1.该农场最可能分布在 A.美国中西部的大平原上 B.澳大利亚大分水岭西
- Mr Brown is one of my friends. He can run very fast and like
- 唐朝和元朝,在中央机构中负责全国行政事务的官僚机构分别是 A.尚书省和门下省 B.中书省和军机处 C.门下省和枢
- 结合下列材料,回答相关问题。 材料一 下图为我国某地区等高线图(单位:m)及冬半年天气系统示意图。材料二 1
- 如果说民主是指一种与个人专制独裁统治不同的、实行“多数人的统治”的国家形式,那么,这个“多数人”指 A. 统治



