九年级(初三)数学下学期下册试题
如图所示的是一个正方体的展开图,把展开图折叠成小正方体,和“强”字一面相对面的字是( )

A . 民
B . 明
C . 文
D . 主
为缓解交通压力,市郊某地正在修建地铁站,拟同步修建地下停车库.如图是停车库坡道入口的设计图,其中MN是水平线,MN∥AD,AD⊥DE,CF⊥AB,垂足分别为D,F,坡道AB的坡度=1:3,AD=9米,点C在DE上,CD=0.5米,CD是限高标志牌的高度(标志牌上写有:限高米).如果进入该车库车辆的高度不能超过线段CF的长,则该停车库限高多少米?(结果精确到0.1米,参考数据:  ≈1.41,
≈1.41,  ≈1.73,
≈1.73, 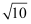 ≈3.16)
≈3.16)
 ≈1.41,
≈1.41,  ≈1.73,
≈1.73, 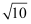 ≈3.16)
≈3.16) 
如图,不是正方体展开图的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D .
如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE.若DE:AC=3:5,则  的值为.
的值为.
 的值为.
的值为.
如图是一个食品包装盒的表面展开图.

-
(1) 请写出包装盒的几何体名称;
-
(2) 根据图中所标尺寸,用a,b表示这个几何体的全面积S(侧面积与底面积之和),并计算当a=1,b=4时,S的值.
若点P(2,6)、点Q(-3,b)都是反比例函数y=  (k≠0)图象上的点,则b=.
(k≠0)图象上的点,则b=.
 (k≠0)图象上的点,则b=.
(k≠0)图象上的点,则b=.
如图所示,大鱼与小鱼是位似图形,则小鱼上的点 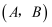 对应大鱼上的点( )
对应大鱼上的点( )
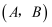 对应大鱼上的点( )
对应大鱼上的点( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
某条道路上通行车辆限速为60千米/时,在离道路50米的点P处建一个监测点,道路AB段为检测区(如图).在△ABP中,已知∠PAB=30°,∠PBA=45°,那么车辆通过AB段的时间在多少秒以内时,可认定为超速(精确到0.1秒)?(参考数据:  ≈1.41,
≈1.41,  ≈1.73,60千米/时=
≈1.73,60千米/时=  米/秒)
米/秒)
 ≈1.41,
≈1.41,  ≈1.73,60千米/时=
≈1.73,60千米/时=  米/秒)
米/秒) 
如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,则S△DOE:S△AOC的值为.

如图,在平面直角坐标系中,正方形  的对角线相交于点
的对角线相交于点  ,将正方形
,将正方形  以
以  为位似中心,
为位似中心, 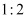 为位似比缩小,点
为位似比缩小,点  的对应点
的对应点 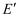 的坐标是
的坐标是
 的对角线相交于点
的对角线相交于点  ,将正方形
,将正方形  以
以  为位似中心,
为位似中心, 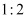 为位似比缩小,点
为位似比缩小,点  的对应点
的对应点 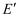 的坐标是
的坐标是 
如图,以O为圆心,AB长为直径作圆,在⊙O上取一点C,延长AB至点D,连接DC,过点A作⊙O的切线交DC的延长线于点E,且∠DCB=∠DAC.

-
(1) 求证:CD是⊙O的切线;
-
(2) 若AD=6,tan∠DCB=
 ,求CE的长.
,求CE的长.
在Rt△ABC中,∠C=90°,BC=3  ,AB=2
,AB=2  ,则∠B的度数为.
,则∠B的度数为.
 ,AB=2
,AB=2  ,则∠B的度数为.
,则∠B的度数为.
如图,已知AB是⊙O的直径,弦CD与直径AB相交于点F.点E在⊙O外,作直线AE,且∠EAC=∠D.

-
(1) 求证:直线AE是⊙O的切线.
-
(2) 若∠BAC=30°,BC=4,cos∠BAD=
 ,CF=
,CF= 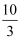 ,求BF的长.
,求BF的长.
如图,直线AD∥BE∥CF,  , DE=6,那么EF的值是 .
, DE=6,那么EF的值是 .
 , DE=6,那么EF的值是 .
, DE=6,那么EF的值是 .
如图,某酒店大门的旋转门内部由三块宽为2米,高为3米的玻璃隔板组成,三块玻璃摆放时夹角相同.若入口处两根立柱之间的距离为2米,则两立柱底端中点到中央转轴底端的距离为( )

A .  米
B . 2米
C . 2
米
B . 2米
C . 2 米
D . 3米
米
D . 3米
 米
B . 2米
C . 2
米
B . 2米
C . 2 米
D . 3米
米
D . 3米
如图是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面与“生”相对应的面上的汉字是( )

A . 活
B . 的
C . 数
D . 学
某校检测学生跳绳水平,抽样调查了部分学生的“1分钟跳绳”成绩,并制成了下面的频数分布直方图(每小组含最小值,不含最大值)和扇形图。

-
(1) D组的人数是人,补全频数分布直方图,扇形图中m=;
-
(2) 本次调查数据中的中位数落在组;
-
(3) 如果“1分钟跳绳”成绩大于或等于120次为优秀,那么该校4500名学生中“1分钟跳绳”成绩为优秀的大约有多少人?
西安世园会标志性雕塑 水龙
水龙 , 内部为钢结构,外包镜面不锈钢,既像一股水花,又似一条飞龙,既蕴含了上善若水的中国传统理念,又有巨龙腾飞的时代精神.小刚同学想利用所学知识测量该雕塑的高度AB,如图,他在距离B点48米的点C处水平放置了一个小平面镜,并沿着BC方向移动,当移动到点E处时,他刚好在小平面镜内看到雕塑的顶端A的像,此时,测得CE=2米,小刚眼晴与地面的距离DE=1.5米.已知点B、C、E在同一水平直线上,且AB⊥BE、DE⊥BE,求雕塑的高度AB.(小平面镜的大小忽略不计)
, 内部为钢结构,外包镜面不锈钢,既像一股水花,又似一条飞龙,既蕴含了上善若水的中国传统理念,又有巨龙腾飞的时代精神.小刚同学想利用所学知识测量该雕塑的高度AB,如图,他在距离B点48米的点C处水平放置了一个小平面镜,并沿着BC方向移动,当移动到点E处时,他刚好在小平面镜内看到雕塑的顶端A的像,此时,测得CE=2米,小刚眼晴与地面的距离DE=1.5米.已知点B、C、E在同一水平直线上,且AB⊥BE、DE⊥BE,求雕塑的高度AB.(小平面镜的大小忽略不计)
 水龙
水龙 , 内部为钢结构,外包镜面不锈钢,既像一股水花,又似一条飞龙,既蕴含了上善若水的中国传统理念,又有巨龙腾飞的时代精神.小刚同学想利用所学知识测量该雕塑的高度AB,如图,他在距离B点48米的点C处水平放置了一个小平面镜,并沿着BC方向移动,当移动到点E处时,他刚好在小平面镜内看到雕塑的顶端A的像,此时,测得CE=2米,小刚眼晴与地面的距离DE=1.5米.已知点B、C、E在同一水平直线上,且AB⊥BE、DE⊥BE,求雕塑的高度AB.(小平面镜的大小忽略不计)
, 内部为钢结构,外包镜面不锈钢,既像一股水花,又似一条飞龙,既蕴含了上善若水的中国传统理念,又有巨龙腾飞的时代精神.小刚同学想利用所学知识测量该雕塑的高度AB,如图,他在距离B点48米的点C处水平放置了一个小平面镜,并沿着BC方向移动,当移动到点E处时,他刚好在小平面镜内看到雕塑的顶端A的像,此时,测得CE=2米,小刚眼晴与地面的距离DE=1.5米.已知点B、C、E在同一水平直线上,且AB⊥BE、DE⊥BE,求雕塑的高度AB.(小平面镜的大小忽略不计)
在平面直角坐标系中,已知  ,
,  ,点
,点  从点
从点  开始沿
开始沿  边向点
边向点  以
以  的速度移动;点
的速度移动;点  从点
从点  开始沿
开始沿 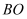 边向点
边向点  以
以  的速度移动.如果
的速度移动.如果  、
、  同时出发,用
同时出发,用  表示移动的时间
表示移动的时间  ,
,
 ,
,  ,点
,点  从点
从点  开始沿
开始沿  边向点
边向点  以
以  的速度移动;点
的速度移动;点  从点
从点  开始沿
开始沿 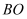 边向点
边向点  以
以  的速度移动.如果
的速度移动.如果  、
、  同时出发,用
同时出发,用  表示移动的时间
表示移动的时间  ,
, 
-
(1) 用含
 的代数式表示:线段
的代数式表示:线段  ;
;  ;
;  .
.
-
(2) 当
 与
与 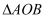 相似时,求出
相似时,求出  的值.
的值.
如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB点F,连接BE.

-
(1) 求证:AC平分∠DAB;
-
(2) 求证:PC=PF;
-
(3) 若tan∠ABC=
 ,AB=14,求线段PC的长.
,AB=14,求线段PC的长.
最近更新
- 在探究平面镜成像特点的过程中,小明把四个模型分别面对玻璃直立在桌面上,用于研究像与物左右位置的关系,其中能够达到实验目的
- 暖国的雨,向来没有变过冰冷的坚硬的灿烂的雪花。博识的人们觉得他单调,他自己也以为不幸否耶?江南的雪,可是滋润美艳之至了;
- 切取一段葡萄的枝条,插入潮湿的沙土中,不久枝条的下端长出了根,这种繁殖方法叫( ) A.扦插
- 若要在普通显微镜下观察到质壁分离、RNA和脂肪,下列四组材料中应选择的一组是( ) A.水稻胚乳和花生子叶 B.天
- 有一瓶14%的氢氧化钾溶液,加热蒸发掉100g水后,得到28%的氢氧化钾溶液80mL,所得溶液的浓度为 A.5mol/
- 下列叙述中,不正确的是 ( ) A.乙烯和甲烷可用酸性高锰酸钾溶液鉴别 B.浓硝酸沾到皮肤上
- 图4为“四个国家1960年和2011年人口数量状况分布示意图”。读图回答1-2题。1.有关四个国家人口增长特点的叙述,正
- 1991年卢瑟福依据α粒子散射实验中α粒子发生了____(选填“大”或“小”)角度散射现象,提出了原子的核式结构模型.
- 根据下面一段文字,在“设计理念”“住宅特点”下的方框内填写恰当的词语。(每空4-6个字)(4分) 设计理想住宅,应从
- 单词拼写与运用;根据句意和首字母(或汉语)提示填空,使句子内容完整1. I can't________(许诺),but
- ______ I enjoy thebook with some nice pictures, I don’t have
- 已知两圆的半径分别是一元二次方程的两个根,若这两个圆的圆心距为5,则这两个圆的位置关系是 ( ) A.相离
- 宋太祖对土地兼并的态度是 ( ) A.限制土地兼并 B.“不抑(土地)兼并” C.土地收归国有 D.制止土地买卖
- 如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,线段AB为半圆O的直径,将Rt△ABC沿射线AB方向平移,
- 用天平和量筒测定矿石的密度。把矿石放在调节好的托盘天平的左盘中,当天平衡时,右盘中的砝码以及游码在标尺上的位置如图所示。
- 据报道,1995年我国科研人员在兰州首次合成了镤元素的一种同位素镤239,并测知其原子核内有148个中子。现有A元素的一
- 如图甲所示,在粗糙水平面上静置一个截面为等腰三角形的斜劈A,其质量为M,两个底角均为300.两个完全相同的、质量均为m
- 图中A~F为初中化学常见的六种物质,其中A、B、D含相同的阴离子,C、D、E、F含有同一种元素,C、E、F是不同类别的
- 阅读下面一则材料,回答问题。 (许衡)尝暑中过河阳,渴甚,道有梨,众争取啖之,衡独危坐树下自若。或问之,曰:“非其有而取
- 下列有关命题的说法中错误的是 ( ) A.若为假命题,则、



