九年级(初三)数学下学期下册试题
如图,  中,点D,E分别在边
中,点D,E分别在边  ,
,  的反向延长线上,且
的反向延长线上,且 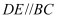 .若
.若  ,
,  ,
,  ,则
,则  为( )
为( )
 中,点D,E分别在边
中,点D,E分别在边  ,
,  的反向延长线上,且
的反向延长线上,且 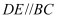 .若
.若  ,
,  ,
,  ,则
,则  为( )
为( ) 
A . 9
B . 6
C . 3
D . 

如图,学校有一旗杆AB.为了测量旗杆高度,小明采用如下方案:在点C处测得旗杆顶B的仰角为45°,从与点C相距6 m的E处测得旗杆顶B的仰角为60°.若CD=EF=1.9 m,求旗杆AB的高度(精确到0.1 m).(参考数据:  ≈1.41,
≈1.41,  ≈1.73.)
≈1.73.)
 ≈1.41,
≈1.41,  ≈1.73.)
≈1.73.)

如图,甲乙两人在游泳池A处发现游泳池中的P处有人求救,甲立即跳入池中去救人,速度为1米/秒,乙以3.5米/秒的速度沿游泳池边跑到距A不远处的B处,捡起一个游泳圈再跳入池中去救人,甲游了20秒到达P处,两秒后乙到达P处.若∠PAB与∠PBC互余,且cos∠PBC=  ,求乙的游泳速度.
,求乙的游泳速度.
 ,求乙的游泳速度.
,求乙的游泳速度. 
如图①所示的组合几何体,它的下面是一个长方体,上面是一个圆柱.

(1)图②和图③是它的两个视图,在横线上分别填写两种视图的名称(填“主”、“左”或“俯”);
(2)根据两个视图中的尺寸,计算这个组合几何体的体积.(结果保留π)
如图是一个正方体的展开图,则在原正方体中,与“青”字相对的字是( )

A . 共
B . 建
C . 绿
D . 水
计算:sin218°+cos45°•tan25°•tan65°+sin72°•cos18°.
如图:为了测量河对岸旗杆AB的高度,在点C处测得顶端A的仰角为30°,沿CB方向前进20m达到D处,在D点测得旗杆顶端A的仰角为45°,则旗杆AB的高度为m.(精确到0.1m)

如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AD=2,DB=4,则  的值为( )
的值为( )
 的值为( )
的值为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知  ,则k的值是.
,则k的值是.
 ,则k的值是.
,则k的值是.
已知y与(2x+1)成反比例,且当x=1时,y=2,那么当x=0时,y=.
如图,函数y=x的图象与函数y=  (x>0)的图象相交于点P(2,m).
(x>0)的图象相交于点P(2,m).
 (x>0)的图象相交于点P(2,m).
(x>0)的图象相交于点P(2,m). 
-
(1) 求m,k的值;
-
(2) 直线y=4与函数y=x的图象相交于点A,与函数y=
 (x>0)的图象相交于点B,求线段AB长.
(x>0)的图象相交于点B,求线段AB长.
下面几何体的表面不能展开成平面的是 ( )
A . 正方体
B . 圆柱
C . 圆锥
D . 球
计算:  +tan60°.
+tan60°.
 +tan60°.
+tan60°.
(阅读理解)如图1,在平面直角坐标系中,直线  的函数关系式
的函数关系式  ,
,  ,
,  是直线
是直线  上任意两个不同的点,过点
上任意两个不同的点,过点  、
、  分别作
分别作  轴、
轴、  轴的平行线交于点
轴的平行线交于点  ,则线段
,则线段  ,于是有
,于是有  ,即
,即  的值仅与
的值仅与  的值有关,不妨称
的值有关,不妨称  为直线
为直线  的“纵横比”.
的“纵横比”.
 的函数关系式
的函数关系式  ,
,  ,
,  是直线
是直线  上任意两个不同的点,过点
上任意两个不同的点,过点  、
、  分别作
分别作  轴、
轴、  轴的平行线交于点
轴的平行线交于点  ,则线段
,则线段  ,于是有
,于是有  ,即
,即  的值仅与
的值仅与  的值有关,不妨称
的值有关,不妨称  为直线
为直线  的“纵横比”.
的“纵横比”. 


-
(1) (直接应用)
直线
 的“纵横比”为,直线
的“纵横比”为,直线  的“纵横比”为.
的“纵横比”为. -
(2) (拓展提升)
如图2,已知直线
 与直线
与直线  互相垂直,请用“纵横比”原理以及相关的几何知识分析
互相垂直,请用“纵横比”原理以及相关的几何知识分析  与
与  的关系,并加以证明.
的关系,并加以证明. -
(3) (综合应用)
如图3,已知点
 ,
,  是
是  轴上一动点,线段
轴上一动点,线段  绕着点
绕着点  按逆时针方向旋转
按逆时针方向旋转  至线段
至线段  ,设此时点
,设此时点  的运动轨迹为直线
的运动轨迹为直线  ,若另一条直线
,若另一条直线  ,且与
,且与 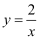 有且只有一个公共点,试确定直线
有且只有一个公共点,试确定直线  的函数关系式.
的函数关系式.
已知:四条线段成比例线段1,2,6,m,则第四比例项m的值是( )
A . 4
B . 8
C . 12
D . 9
如图,△ABC中,D为BC上一点,∠BAD=∠C,AB=6,BD=4,则CD的长为.

如图,某旅游景区为方便游客,修建了一条东西走向的木栈道AB,在景区道路CD的C处测得栈道一端A位于北偏西42°方向,另一端B位于北偏东45°方向,又测得AC为100米,求木栈道AB的长度(结果保留整数。参考数据:sin42°≈  ,cos42°≈
,cos42°≈  ,tan42°≈
,tan42°≈ 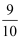 )。
)。
 ,cos42°≈
,cos42°≈  ,tan42°≈
,tan42°≈ 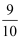 )。
)。 
如图,点A、B、C都在格点上,则∠CAB的正切值为.

如图,在边长为1的小正方形组成的网格中,给出了格点四边形ABCD(顶点为网格线的交点).

(1)画出四边形ABCD关于x轴成轴对称的四边形A1B1C1D1;
(2)以O为位似中心,在第三象限画出四边形ABCD的位似四边形A2B2C2D2 , 且位似比为1;
(3)在第一象限内找出格点P,使∠DCP=∠CDP,并写出点P的坐标(写出一个即可).
如图,  三个顶点的坐标分别为
三个顶点的坐标分别为  ,
,  ,
,  ,以原点O为位似中心,画出一个三角形,使它与
,以原点O为位似中心,画出一个三角形,使它与  的相似比为
的相似比为  .则画出的一个三角形为.
.则画出的一个三角形为.
 三个顶点的坐标分别为
三个顶点的坐标分别为  ,
,  ,
,  ,以原点O为位似中心,画出一个三角形,使它与
,以原点O为位似中心,画出一个三角形,使它与  的相似比为
的相似比为  .则画出的一个三角形为.
.则画出的一个三角形为. 
最近更新
- 1. 叶肉细胞中能同时进行多步骤的两个过程,即CO2+H2O (CH2O)+O2,请回答: (1)过程
- 下列物质中,前者属于纯净物,后者属于混合物的是() A.净化后的空气;氧化镁 B.水和冰混合;澄清石灰水 C.生锈的铁钉
- 氮氧化铝(AlON)属原子晶体,是一种超强透明材料,下列描述错误的是 A.AlON和石英的化学键类型相同 B.AlON和
- 设复数z满足i(z-4)=3+2i(i是虚数单位),则z的虚部为.
- 将足量BaCO3分别加入:① 30mL 水 ②10mL 0.2mol/LNa2CO3溶液 ③50mL 0.01mo
- --_______________________________? -- Show me the latest sca
- 已知在⊿ABC中,∠A=50°,∠B=35°,那么与∠C相邻的外角为_______度.
- 下列各句中加点的成语使用恰当的一项是( ) A.受保护的野生动物曾一度从市场上消失,但SARS过后,在广东很快又东
- 四边形内接于是的直径,.(1)如图1,求证; (2)过点D作的切线,交延长线于点P(如图2).,求的长.
- 某个婴儿不能消化乳糖,经检查发现,他的乳糖酶分子有一个氨基酸改换而导致乳糖酶失活,发生这种现象的根本原因是 ( )
- 2010年3月28日,山西王家岭煤矿发生透水事故。在救援过程中,救援人员钻了两个“生 命之孔”,及时向被困人员输送营
- 27、右图是人类遗传病系谱图,I—l是纯合子。该病的致病基因可能是( )①Y染色体上的基因 ②X染色体上的隐性基因 ③X
- 北京奥运会颁奖礼仪服装共有16款,“青花瓷”系列被认为最富有中国情调,其设计灵感取自中国青花瓷器。韵味传神的“青花瓷”礼
- 如图所示,“神舟”飞船升空后,进入近地点为B,远地点为A的椭圆轨道I上飞行。飞行数圈后变轨.在过远地点A的圆轨道Ⅱ上做匀
- 下列各句中,没有语病的一句是 ( ) A.我省在对口支援四川松潘重建中本着对历史负责、对灾区群众负责
- .已知与内切,若的半径为3cm,的半径为6cm,那么两圆的圆心距的长是 .
- 数列{an}:1,-,,-,…的一个通项公式是()
- 满足条件{2,5}S={2,3,5}的所有集合S的个数是( ) A、1 B、2 C、3
- 已知两圆的半径分别为2和3,圆心距为5,则这两圆的位置关系是 ( ) A.外离
- (2009四川卷文)如图,在半径为3的球面上有三点,=90°,, 球心O到平面的距离是,则两点的球面距离是



