九年级(初三)数学下学期下册试题
如图,在平面直角坐标系中,O为坐标原点,点A,B在函数 
 的图象上(点B的横坐标大于点A的横坐标),点A的坐示为
的图象上(点B的横坐标大于点A的横坐标),点A的坐示为  ,过点A作
,过点A作  轴于点D,过点B作
轴于点D,过点B作  轴于点C,连接
轴于点C,连接  ,
,  .
.

 的图象上(点B的横坐标大于点A的横坐标),点A的坐示为
的图象上(点B的横坐标大于点A的横坐标),点A的坐示为  ,过点A作
,过点A作  轴于点D,过点B作
轴于点D,过点B作  轴于点C,连接
轴于点C,连接  ,
,  .
. 
-
(1) 求k的值.
-
(2) 若D为
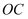 中点,求四边形
中点,求四边形 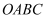 的面积.
的面积.
下面的三视图对应的物体是( )

A .  B .
B .  C .
C .  D .
D . 
 C .
C .
如图,已知双曲线 和
和 , 直线OA与双曲线
, 直线OA与双曲线 交于点A,将直线OA向下平移与双曲线
交于点A,将直线OA向下平移与双曲线 交于点B,与y轴交于点P,与双曲线
交于点B,与y轴交于点P,与双曲线 交于点C,若S△ABC=10,
交于点C,若S△ABC=10, , 则k的值为( )
, 则k的值为( )
 和
和 , 直线OA与双曲线
, 直线OA与双曲线 交于点A,将直线OA向下平移与双曲线
交于点A,将直线OA向下平移与双曲线 交于点B,与y轴交于点P,与双曲线
交于点B,与y轴交于点P,与双曲线 交于点C,若S△ABC=10,
交于点C,若S△ABC=10, , 则k的值为( )
, 则k的值为( ) 
A . -4
B . 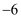 C .
C .  D .
D . 
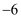 C .
C .  D .
D . 
计算题。
-
(1) 计算:
 .
.
-
(2) 先化简,再求值:
 ,其中x=
,其中x=  ﹣3.
﹣3.
已知∠A为锐角,若cosA=sin65°,则∠A的度数为.
计算:(2020﹣π)0﹣2cos30°+ 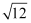 +(﹣
+(﹣  )﹣1.
)﹣1.
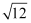 +(﹣
+(﹣  )﹣1.
)﹣1.
如图,张华同学在学校某建筑物顶楼的点C处测得正前方小山包上旗杆顶部A点的仰角为26°,旗杆底部B点的俯角为45°,若小山包底部点E到建筑物的水平距离DE=10米.(说明:CD⊥DE于点D,点A、点B、点E在同一直线上,且AE⊥DE于点E)
-
(1) 求旗杆AB的高.(结果精确到0.1米)
-
(2) 若旗杆底部点B与小山包坡底点F所形成的斜坡BF的坡比i=1:
 ,且测得DF=6米,求建筑物的高.(结果精确到0.1米,参考数据:sin26°≈0.438,cos26°≈0.899,tan26°≈0.487,
,且测得DF=6米,求建筑物的高.(结果精确到0.1米,参考数据:sin26°≈0.438,cos26°≈0.899,tan26°≈0.487,  ≈1.414)
≈1.414)
如图,在△ABC中,D、E为边AB的三等分点,EF∥DG∥AC,H为AF与DG的交点.若AC=12,则DH=.

已知△ABC∽△DEF,若△ABC与△DEF的相似比为3∶4,则△ABC与△DEF的面积比为.
如图,在A点有一个热气球,由于受西风的影响,以20米/分的速度沿与地面成  角的方向飞行,10分钟后到达C处,此时热气球上的人测得地面上的B点俯角为
角的方向飞行,10分钟后到达C处,此时热气球上的人测得地面上的B点俯角为  ,则A、B两点间的距离为米.
,则A、B两点间的距离为米.
 角的方向飞行,10分钟后到达C处,此时热气球上的人测得地面上的B点俯角为
角的方向飞行,10分钟后到达C处,此时热气球上的人测得地面上的B点俯角为  ,则A、B两点间的距离为米.
,则A、B两点间的距离为米. 
已知α是锐角且tanα= , 则sinα+cosα=
, 则sinα+cosα=
 , 则sinα+cosα=
, 则sinα+cosα=
如图,  是圆
是圆  的直径,
的直径,  与
与  交于点
交于点  .如果
.如果  ,那么
,那么  的长为.
的长为.
 是圆
是圆  的直径,
的直径,  与
与  交于点
交于点  .如果
.如果  ,那么
,那么  的长为.
的长为. 
如图.在□ABCD中,点E在边BC上,点F在边AD的延长线上,且DF=BE.EF与CD交于点G.若  ,BE=4,求BC的长.
,BE=4,求BC的长.
 ,BE=4,求BC的长.
,BE=4,求BC的长. 
下列各线段的长度成比例的是( )
A . 2、5、6、8
B . 1、2、3、4
C . 3、6、7、9
D . 3、6、9、18
已知点A(2,﹣3)在双曲线y=  上,则下列哪个点也在此双曲线上( )
上,则下列哪个点也在此双曲线上( )
 上,则下列哪个点也在此双曲线上( )
上,则下列哪个点也在此双曲线上( )
A . (1,6)
B . (﹣1,6)
C . (2,3)
D . (﹣2,﹣3)
李华为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15  .(sin15°=0.259,cos15°=0.966,tan15°=0.268,结果精确到0.1m)
.(sin15°=0.259,cos15°=0.966,tan15°=0.268,结果精确到0.1m)
 .(sin15°=0.259,cos15°=0.966,tan15°=0.268,结果精确到0.1m)
.(sin15°=0.259,cos15°=0.966,tan15°=0.268,结果精确到0.1m) 
-
(1) 求李华此时与地面的垂直距离CD的值;
-
(2) 李华的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45
 ,求楼房AB的高度.
,求楼房AB的高度.
如图为某物体简化的主视图和俯视图,猜想该物体可能是( )

A . 光盘
B . 双层蛋糕
C . 游泳圈
D . 铅笔
将如图所示的图形剪去两个小正方形,使余下的部分图形恰好能折成一个正方体,应剪去的两个小正方形可以是( )

A . ②③
B . ①⑥
C . ①⑦
D . ②⑥
如图,△  ∽△
∽△ 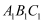 ,那么它们的相似比是;
,那么它们的相似比是;
 ∽△
∽△ 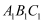 ,那么它们的相似比是;
,那么它们的相似比是;
平面直角坐标系xOy中,点P(a,b)经过某种变换后得到的对应点为P′(  a+1,
a+1,  b﹣1).已知A,B,C是不共线的三个点,它们经过这种变换后,得到的对应点分别为A′,B′,C′.若△ABC的面积为S1 , △A′B′C′的面积为S2 , 则用等式表示S1与S2的关系为( )
b﹣1).已知A,B,C是不共线的三个点,它们经过这种变换后,得到的对应点分别为A′,B′,C′.若△ABC的面积为S1 , △A′B′C′的面积为S2 , 则用等式表示S1与S2的关系为( )
 a+1,
a+1,  b﹣1).已知A,B,C是不共线的三个点,它们经过这种变换后,得到的对应点分别为A′,B′,C′.若△ABC的面积为S1 , △A′B′C′的面积为S2 , 则用等式表示S1与S2的关系为( )
b﹣1).已知A,B,C是不共线的三个点,它们经过这种变换后,得到的对应点分别为A′,B′,C′.若△ABC的面积为S1 , △A′B′C′的面积为S2 , 则用等式表示S1与S2的关系为( )
A . S1  S2
B . S1
S2
B . S1  S2
C . S1=2S2
D . S1=4S2
S2
C . S1=2S2
D . S1=4S2
 S2
B . S1
S2
B . S1  S2
C . S1=2S2
D . S1=4S2
S2
C . S1=2S2
D . S1=4S2
最近更新
- 九是中国古代最高统治者的专属数字。西周时期只有天子可用九鼎,后世只有皇帝的龙袍可绣九条金龙,明清时期只有皇宫屋檐可有九只
- 最后的黄豆 爷爷是染布的。他爱吃黄豆出了名。在镇子西头,爷爷十七岁那年刷刷地在地上架起了好几口大染锅。这吃饭的手艺是“偷
- 1919 年 12 月,胡适在 《新青年》 上发表 《“新思潮”的意义》 一文,倡导“整理国 故”运动。“就是从乱七八糟
- (24分)物理小组的同学在寒冷的冬天做了一个这样的实验:他们把一个实心的大铝球加热到某温度,然后把它放在结冰的湖面上(冰
- 某有机物A 是农药生产中的一种中间体,其结构简式如下。下列叙述中正确的是A.1 mo1 A最多能与4 mol H2发生加
- 下列各组物质中不管以何种比例混合,只要总质量一定,充分燃烧后生成的二氧化碳的量不变的是() A 乙炔和乙烯
- 已知:a、b、c分别为△ABC的三边长,a=5,且+(b-c+1)2=0,则△ABC的面积为________个平方单位.
- 对绿色植物根尖细胞某细胞器的组成成分进行分析,发现A、T、C、G、U五种碱基,则在完全在该细胞器中完成的生理活动是(
- 阅读下面这首诗,完成1—2题。 宿骆氏亭寄怀崔雍崔衮 李商隐 竹坞无尘水槛清,相思迢递隔重城。 秋阴不散霜飞晚,留得枯荷
- The goals_________ he had fought all his life no longer seem
- 最先利用扭秤实验较精确测出万有引力常量G的科学家是 ( ) (A)库仑 (B)牛顿 (C)卡文迪
- ---My god, it’s raining again. What a cold day! ---So it
- 下图为有髓神经纤维的局部,被髓鞘细胞包裹的轴突区域(b、d)钠、钾离子不能进出细胞,裸露的轴突区域(a、c、e)钠、钾离
- 请选择下列划线词语注音完全正确的一组( )(2分)A 倔强 juè 洗濯zhuó 诅咒zǔ 获益匪浅 fēi
- 读下图完成1﹣5题.1.请根据如图判断:从南北半球来看,我国位于( )半球. A.东 B.
- We can’t do it________ your help. A. with B.of C. under D
- 关于功和动能的变化,下列说法中正确的是( )A.物体在力的方向上发生了位移,该力一定对物体做了功B.只要有力对物体
- 指出句中活用的词,并说明用法和意义 臂非加长也,而见者远
- 在△ABC中,∠C=90°,,,则k的值是 A.5 B.-5 C.D.
- 如图所示的实验,可以用来说明物质的某种物理性质.图中的磁体将大头针吸起,表明磁体有_________________;图



