九年级(初三)数学下学期下册试题
如图,P是∠α的边OA上一点,且点P的横坐标为3,sinα=  ,则tanα=( )
,则tanα=( )
 ,则tanα=( )
,则tanα=( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图, 是等腰直角三角形,AD是其斜边BC上的高,点E是AD上的一点,以CE为边向上作等边
是等腰直角三角形,AD是其斜边BC上的高,点E是AD上的一点,以CE为边向上作等边 , 连接BF.
, 连接BF.
 是等腰直角三角形,AD是其斜边BC上的高,点E是AD上的一点,以CE为边向上作等边
是等腰直角三角形,AD是其斜边BC上的高,点E是AD上的一点,以CE为边向上作等边 , 连接BF.
, 连接BF.
-
(1) 如图1,求
 的度数;
的度数;
-
(2) 连接AF,如图2,若
 , BF与AC交于点G.
, BF与AC交于点G.①证明:AF2=AG
 AB;
AB;②若BC=2,求FG的长.
长方体的主视图、俯视图如图所示(单位:m),则其左视图的面积是( )

A . 4 m2
B . 12 m2
C . 1 m2
D . 3 m2
如图,在Rt△ABC中,∠ABC=90°,A(1,0),B(0,4),反比例函数y═  的图象过点C,边AC与y轴交于点D,若S△BAD:S△BCD=1:2,则k=( ).
的图象过点C,边AC与y轴交于点D,若S△BAD:S△BCD=1:2,则k=( ).
 的图象过点C,边AC与y轴交于点D,若S△BAD:S△BCD=1:2,则k=( ).
的图象过点C,边AC与y轴交于点D,若S△BAD:S△BCD=1:2,则k=( ).

A . ﹣4
B . ﹣6
C . ﹣7
D . ﹣8
下列各组线段中,不成比例的是( )
A . 4cm,10cm,6cm,8cm
B . 12cm,4cm,6cm,8cm
C . 33cm,11cm,22cm,66cm
D . 2cm,4cm,4cm,8cm
小宇想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A、B两点的距离.

如图所示的几何体的左视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
计算:  .
.
 .
.
列出下列问题中的函数关系式,并判断它们是否为反比例函数.
-
(1) 某农场的粮食总产量为1 500t,则该农场人数y(人)与平均每人占有粮食量x(t)的函数关系式;
-
(2) 在加油站,加油机显示器上显示的某一种油的单价为每升4.75元,总价从0元开始随着加油量的变化而变化,则总价y(元)与加油量x(L)的函数关系式;
-
(3) 小明完成100m赛跑时,时间t(s)与他跑步的平均速度v(m/s)之间的函数关系式.
若点  ,
,  ,
,  都在反比例函数
都在反比例函数  的图象上,则
的图象上,则  ,
,  ,
,  的大小关系是( )
的大小关系是( )
 ,
,  ,
,  都在反比例函数
都在反比例函数  的图象上,则
的图象上,则  ,
,  ,
,  的大小关系是( )
的大小关系是( )
A . 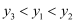 B .
B .  C .
C .  D .
D . 
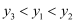 B .
B .  C .
C .  D .
D . 
如图,A,B是反比例函数  图象上的两点,过点A,B分别作x轴的平行线交y轴于点C,D,直线AB交y轴正半轴于点E.若点B的横坐标为5,
图象上的两点,过点A,B分别作x轴的平行线交y轴于点C,D,直线AB交y轴正半轴于点E.若点B的横坐标为5,  ,
,  ,则k的值为( )
,则k的值为( )
 图象上的两点,过点A,B分别作x轴的平行线交y轴于点C,D,直线AB交y轴正半轴于点E.若点B的横坐标为5,
图象上的两点,过点A,B分别作x轴的平行线交y轴于点C,D,直线AB交y轴正半轴于点E.若点B的横坐标为5,  ,
,  ,则k的值为( )
,则k的值为( ) 
A . 5
B . 4
C . 3
D . 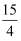
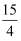
如图,以等边三角形ABC的BC边为直径画半圆,分别交AB,AC于点E,D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为( )

A . 4
B .  C . 6
D .
C . 6
D . 
 C . 6
D .
C . 6
D . 
已知反比例函数的图象经过P(-2·3).
-
(1) 求此反比例函数的解析式;
-
(2) 点A(2.-3)、B(3,2)是否在这个函数的图象上?
-
(3) 这个函数的图象位于哪些象限?函数值y随自变量x的减小如何变化?
如图,CD是Rt△ABC斜边AB上的高,CD=6,BD=4,则AB的长为( )

A . 11
B . 12
C . 13
D . 14
如图,直线 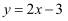 与x,y轴分别交于点B,点A,与反比例函数
与x,y轴分别交于点B,点A,与反比例函数  的图象交于点C,若
的图象交于点C,若  ,则k的值为( )
,则k的值为( )
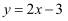 与x,y轴分别交于点B,点A,与反比例函数
与x,y轴分别交于点B,点A,与反比例函数  的图象交于点C,若
的图象交于点C,若  ,则k的值为( )
,则k的值为( ) 
A . 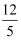 B .
B .  C .
C .  D .
D . 
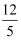 B .
B .  C .
C .  D .
D . 
如图,在平面直角坐标系中,等腰三角形ABC的顶点A在y轴上,底边AB//x轴,顶点B、C在函数  的图象上.若
的图象上.若  ,点A的纵坐标为1,则k的值为.
,点A的纵坐标为1,则k的值为.
 的图象上.若
的图象上.若  ,点A的纵坐标为1,则k的值为.
,点A的纵坐标为1,则k的值为.
如图是一个三棱柱.下列图形中,能通过折叠围成一个三棱柱的是( )
![]()
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D .
如图,阳光通过窗口照到室内,在地面上留下1.6m宽的亮区DE , 已知亮区一边到窗下的墙脚距离CE=3.6m,窗高AB=1.2m,那么窗口底边离地面的高度BC=m.

用计算器求下列锐角三角函数值:

在同一直角坐标系中,函数y=kx+1与  (k≠0)的图象大致是( )
(k≠0)的图象大致是( )
 (k≠0)的图象大致是( )
(k≠0)的图象大致是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
最近更新
- 如图所示,用单摆测重力加速度,其中L0、d、n、t分别表示实验时已测得的数据。 根据这些数据可以算出:悬线长度(m)
- 杜甫《旅夜书怀》中以雄浑阔大的景来反衬诗人孤苦渺小、孤寂无依,同时又用江流暗示岁月流逝而言人到垂暮之年身世凄凉之悲的两句
- 已知函数y=g(x)的图象与函数y=3x的图象关于直线y=x对称, 则g(2)的值为(). A.9 B.
- 下列关于化学平衡常数的说法中错误的是: A.化学平衡常数K只与温度有关,随温度的升高,K可能增大、减小或不变 B.
- 飞机以恒定的速度沿水平方向飞行,距地面的高度为H=500m,在飞行过程中释放一个炸弹,炸弹着地即刻爆炸,爆炸声向各个方向
- 热核反应是一种理想能源的原因是 ( ) A.就平均每一个核于来说,热核反应比重核裂变时释放的能量多 B.
- 离散型随机变量的标准差反映了随机变量取值偏离于 的平均程度,标准差越小,则随机变量偏离于均值的
- 病毒在结构上的特点是 ( ) A.无细胞结构 B.无细胞壁 C.无液泡和叶绿体 D.无成
- 下列离子方程式书写正确的是() A.向NaHSO4溶液加入Ba(OH)2溶液至中性:H++SO+Ba2++OH-===B
- --- I am sorry I stepped outside for a smoke. I am very tire
- 阅读下面一首诗,然后回答1-2题。 春 日 秦 观 一夕轻雷落万丝,霁光浮瓦碧参差。 有情芍药含春泪,无力蔷
- 反应A(g)+3B(g)2C(g)+2D(g),在四种不同情况下用不同物质表示的反应速率分别如下,其中反应速率最大的是
- 下列叙述中正确的是( ) A.硫燃烧需要先点燃,所以硫燃烧是吸收热量的 B.水蒸气液化放出热量,这是化学反应的放热
- 右图是春节联欢晚会上的舞蹈《飞天》剧照,七年级一班的唐杰一家在观看此节目时, 发出了以下议论,其中存在错误的是(
- 美国约翰·w·梅森在《冷战》一书中指出,如果把冷战时期重新定义为“长时期的和平”倒是颇为令人耳目一新的。文中作者对冷战重
- 下列各组物质,按混合物、化合物、单质的顺序排列的是() A.冰水、干冰、氮气 B.石油、煤、水银 C.洁净的空气、氯化钠
- 下列分子中,所有原子都处在同一平面的是A.2—溴丙烷 B.氯乙烯 C.丙炔 D.甲苯
- 京广线与长江交会于……………………………………………………( ) A、重庆 B、南京
- 科学、合理地减轻体重的方法有 A多运动 B节食、只喝水 C少吃高能量的食物 D多吃高
- 下列为某一段多肽链和控制它合成的DNA双链的一段。“-甲硫氨酸-脯氨酸-苏氨酸-甘氨酸-缬氨酸-”。密码表:甲硫氨酸 A



