九年级(初三)数学下学期下册试题
如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80m,DE=10m,求障碍物B,C两点间的距离(结果精确到0.1m)(参考数据:  ≈1.414,
≈1.414,  ≈1.732)
≈1.732)
 ≈1.414,
≈1.414,  ≈1.732)
≈1.732)
如图,G为△ABC的重心,DE过点G,且DE∥BC,交AB、AC,分别于D、E两点,若△ADE的面积为5,则四边形BDEC的面积为.

已知反比例函数y=(a﹣2)  的图象位于第二、四象限,则a的值为( )
的图象位于第二、四象限,则a的值为( )
 的图象位于第二、四象限,则a的值为( )
的图象位于第二、四象限,则a的值为( )
A . 1
B . 3
C . ﹣1
D . ﹣3
如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20m,EC=10m,CD=20m,则河的宽度AB等于( )

A . 60m
B . 40m
C . 30
D . 20m
如图,在△ABC中,AB=AC=5,  ,将△ABC绕点B逆时针旋转,得到
,将△ABC绕点B逆时针旋转,得到  ,当点
,当点  在线段CA延长线上时
在线段CA延长线上时  的面积为.
的面积为.
 ,将△ABC绕点B逆时针旋转,得到
,将△ABC绕点B逆时针旋转,得到  ,当点
,当点  在线段CA延长线上时
在线段CA延长线上时  的面积为.
的面积为. 
如图,该平面展开图按虚线折叠成正方体后,相对面上两个数之和为8,则x+y= .

如图,冬奥会滑雪场有一坡角为20°的滑雪道,滑雪道的长AC为100米,则BC的长为( )米.

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若△ABC∽△DEF,相似比为1︰2,△ABC的面积是3cm2 , 则△DEF的面积是( )
A . 3cm2
B . 6cm2
C . 12cm2
D . 2cm2
如图,在  中,点D在AB上,点E在AC上,
中,点D在AB上,点E在AC上, 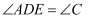 ,若
,若  ,四边形DBCE的面积是
,四边形DBCE的面积是 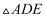 的面积的3倍,则BC的长为.
的面积的3倍,则BC的长为.
 中,点D在AB上,点E在AC上,
中,点D在AB上,点E在AC上, 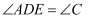 ,若
,若  ,四边形DBCE的面积是
,四边形DBCE的面积是 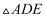 的面积的3倍,则BC的长为.
的面积的3倍,则BC的长为. 
2014年1月,国家发改委出台指导意见,要求2015年底前,所有城市原则上全面实行居民阶梯水价制度.小明为了解市政府调整水价方案的社会反响,随机访问了自己居住在小区的部分居民,就“每月每户的用水量”和“调价对用水行为改变”两个问题进行调查,并把调查结果整理成下面的图1,图2.

小明发现每月每户的用水量在5m2-35m2之间,有8户居民对用水价格调价涨幅抱无所谓,不用考虑用水方式的改变.根据小明绘制的图表和发现的信息,完成下列问题:
-
(1) n=,小明调查了户居民,并补全图1 ;
-
(2) 每月每户用水量的中位数和众数分别落在什么范围?
-
(3) 如果小明所在的小区有1800户居民,请你估计“视调价涨幅采取相应的用水方式改变”的居民户数有多少?
如图,在△ABC中,若DE∥BC, =
= , DE=4cm,则BC的长为 .
, DE=4cm,则BC的长为 .
 =
= , DE=4cm,则BC的长为 .
, DE=4cm,则BC的长为 .
圆锥侧面展开图可能是下列图中的( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
反比例函数y= 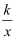 在第一象限的图象如图,请写出一个满足条件的k值,k=
在第一象限的图象如图,请写出一个满足条件的k值,k=
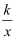 在第一象限的图象如图,请写出一个满足条件的k值,k=
在第一象限的图象如图,请写出一个满足条件的k值,k= 
已知三角函数值,可以先利用计算器求出锐角α与β,从而比较它们的大小.你能否不用计算器来比较以下的锐角α与β的大小?如果能,说说你的想法.
(1)cosα= , tanβ=
, tanβ=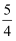 ;
;
(2)sinα=0.456 7,cosβ=0.567 8.
下列几何体中,俯视图为矩形的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  D .
D .
计算:cos230°+2sin60°﹣tan45°.
如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为3米,台阶AC的坡度为1:  (即AB:BC=1:
(即AB:BC=1:  ),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度(侧倾器的高度忽略不计).
),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度(侧倾器的高度忽略不计).

交通安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道上确定点D,使CD与垂直,测得CD的长等于21米,在上点D的同侧取点A、B,使  ,
,  .
.
 ,
,  .
. 
-
(1) 求AB的长(精确到0.1米,参考数据:
 ,
,  );
);
-
(2) 已知本路段对汽车限速为40千米/小时,若测得某辆汽车从A到B用时为2秒,这辆汽车是否超速?说明理由.
雨后初晴,一学生在运动场上玩耍,从他前面2米远一块小积水处,他看到旗杆顶端的倒影,如果旗杆底端到积水处的距离为40米,该生的眼部高度是1.5米,那么旗杆的高度是( )
A . 30米
B . 40米
C . 25米
D . 35米
如图是由一些相同的小正方体组成的几何体的三视图,则组成这个几何体的小正方体个数最多为( )

A . 7
B . 8
C . 9
D . 10
最近更新
- I have a rule for travel: Never carry a map. I prefer to ask
- (08·福建D篇) The global energy crisis isapproaching.What can w
- 小刚同学在做有关溶液性质的实验时,向溶液中滴加过量的溶液。下列图像中能正确表示其变化过程的是
- 有学者认为:“从许许多多不平等条约签订,腐败无能的、以慈禧太后为首的清政府成为列强在华的代理人。他们就像列强手中的木偶,
- 下图表示甲状腺活动调节的示意图。对这一调节的叙述,错误的是( )A.甲与乙结构分别表示下丘脑和垂体 B.a与b物质
- 根据下列事实,写出有关的化学方程式: ⑴金属镁在CO2中燃烧,生成一种白色固体和黑色固体:
- 下列各溶液中,微粒的物质的量浓度关系正确的是A.0.1mol・L-1的(NH4)2SO4溶液中:c(SO42-)>
- 仙人掌生活在缺水的沙漠中,在仙人掌的细胞中含量最多的化合物是( ) A、水 B、脂类
- ---I think Animals world is the best show. --- I don't __
- 双曲线()的左、右顶点分别是,点是双曲线上一点,直线的斜率是,直线与双曲线的一条渐近线垂直,则双曲线的离心率为(
- In the future, the US policy is likely to be strongly determ
- 下列各组词语中,没有错别字的一组是() A.肤浅浏览俯首帖耳沤心沥血 B.防范谗言以儆效尤脸色腊黄 C.宣泄娴雅嗤之以鼻
- 某地建一座桥,两端的桥墩已建好,这两墩相距米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为25
- 右图是一支架(一种小零件),支架的两个台阶的高度和宽度都是同一长度.则它的三视图是
- 一根轻质弹簧一端固定,用大小为F1的力压弹簧的另一端,平衡时长度为l1;改用大小为F2的力拉弹簧,平衡时长度为l2.弹簧
- 阅读下列材料,回答问题。(20分) 材料一 汉武帝时,分全国为十三州,每州置一刺史,监察地方。其督察内容规定六条:“第一
- 一It was really kind of you to give me a lift home. 一Oh,don
- 下列各组中的离子,都能发生水解反应的一组是() A.Na+、Cu2+、Cl-、ClO- B.Ca2+、Zn2+、、S2-
- 2017年4月22日货运飞船“天舟一号”升入太空和“天宫二号”完成第一次交会对接。高氯酸钾(KClO4)可用作火箭推进剂
- 在某条铁路列车的窗口依次可以看到:广阔的麦田、套种的棉花;摆着的红枣、花生、苹果的商亭;捕鱼捞虾、采摘桑叶的农事活动;基



