九年级(初三)数学下学期下册试题
圆锥形礼帽的底面半径为9cm,母线长为30cm,则这个圆锥形礼帽的侧面积为.
如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x(x≥0),则x的取值范围是.

如图,在Rt△ABC中,∠C=90°,点D在边AB上,线段DC绕点D逆时针旋转,端点C恰巧落在边AC上的点E处.如果 =m,
=m, =n.那么m与n满足的关系式是:m=(用含n的代数式表示m).
=n.那么m与n满足的关系式是:m=(用含n的代数式表示m).
 =m,
=m, =n.那么m与n满足的关系式是:m=(用含n的代数式表示m).
=n.那么m与n满足的关系式是:m=(用含n的代数式表示m). 
如图,平面直角坐标系中,点  分别在函数
分别在函数  与
与  的图象上,点P在x轴上.若
的图象上,点P在x轴上.若  轴,则
轴,则  的面积为.
的面积为.
 分别在函数
分别在函数  与
与  的图象上,点P在x轴上.若
的图象上,点P在x轴上.若  轴,则
轴,则  的面积为.
的面积为.

在小明住的小区有一条笔直的路,路中间有一盏路灯,一天晚上,他行走在这条路上,如图,当他从A点走到B点的过程,他在灯光照射下的影长l与所走路程s的变化关系图象大致是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在高为60米的小山上,测得山底一座楼房的顶端和底部的俯角分别为30°和60°,则这座楼房的高为.
如图,在昆明市轨道交通的修建中,规划在A、B两地修建一段地铁,点B在点A的正东方向,由于A、B之间建筑物较多,无法直接测量,现测得古树C在点A的北偏东45°方向上,在点B的北偏西60°方向上,BC=400m,请你求出这段地铁AB的长度.(结果精确到1m,参考数据:  ,
,  ≈1.732)
≈1.732)
 ,
,  ≈1.732)
≈1.732) 
圆锥底面圆的半径为3m,其侧面展开图是半圆,则圆锥母线长为 m.
已知△ABC在坐标平面内三顶点的坐标分别为A(0,2)、B(3,3)、C(2,1).以B为位似中心,画出与△ABC相似(与图形同向),且相似比是3的三角形,它的三个对应顶点的坐标分别是 .

如图,△ABC中,DE//BC,EF//A
B.求证:△ADE∽△EFC.

在一空旷场地上设计一落地为矩形ABCD的小屋,AB+BC=8m.拴住小狗的8m长的绳子一端固定在B点处,小狗在不能进入小屋内的条件下活动,其可以活动的区域面积为S(m2).

如图1,若BC=2m,则S=m2.
如图2,现考虑在(1)中的矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域,使之变成落地为五边形ABCED的小屋,其它条件不变.则在BC的变化过程中,当S取得最小值时,边BC的长为m.
一个几何体从正面、左面、上面看到的平面图形都是圆,则这个几何体是;
如图,已知第一象限内的点A在反比例函数y=  上,第二象限的点B在反比例函数y=
上,第二象限的点B在反比例函数y=  上,且OA⊥OB,tanA=
上,且OA⊥OB,tanA=  ,则k的值为.
,则k的值为.
 上,第二象限的点B在反比例函数y=
上,第二象限的点B在反比例函数y=  上,且OA⊥OB,tanA=
上,且OA⊥OB,tanA=  ,则k的值为.
,则k的值为. 
若α为锐角,且tanα= ,则有( )
,则有( )
 ,则有( )
,则有( )
A . 0°<α<30°
B . 30°<α<45°
C . 45°<α<60°
D . 60°<α<90°
下列图形中,是相似形的是( )
A . 所有平行四边形
B . 所有矩形
C . 所有菱形
D . 所有正方形
两个直角三角形按如图方式摆放,若AD=10,BE=6,∠ADE=37°,∠BCE=29°. 求CD长(精确到0.01).
(sin37°≈0.602,cos37°≈0.799,tan37°≈0.754,sin29°≈0.485,cos29°≈0.875,tan29°≈0.554)
如图,直线 l1 ∥l2 ∥l3 ,直线 AC 分别交 l1 , l2 , l3 于点 A,B,C;直线 DF 分别交 l1 , l2 , l3 于点 D,E,F,AC 与 DF 相交于点 G,且 AG=2,GB=1,BC=5,则  的值是( )
的值是( )
 的值是( )
的值是( ) 
A .  B . 2
C .
B . 2
C .  D .
D . 
 B . 2
C .
B . 2
C .  D .
D . 
如图,矩形EFGH的四个顶点分别在菱形ABCD的四条边上,BE=BF.将△AEH,△CFG分别沿边EH,FG折叠,当重叠部分为菱形且面积是菱形ABCD面积的 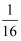 时,则
时,则  为( )
为( )
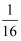 时,则
时,则  为( )
为( ) 
A . 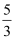 B . 2
C .
B . 2
C .  D . 4
D . 4
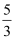 B . 2
C .
B . 2
C .  D . 4
D . 4
梅沙海滨公园沙滩的某一段可近似看成是一条直线段。救生员甲正在岸边A处巡查,发现海中B处有人求救,甲救生员并没有从A处下水去救人,而是沿着岸边从A处跑到离B处最近的D处,然后游向B处.若甲救生员在岸边奔跑的速度为6米/秒,在海水中游泳的速度是2米/秒且AD=BD=300米.(参考数据:  )
)
 )
)
-
(1) 试分析,甲救生员的选择是否正确;
-
(2) 若此时救生员乙恰好在C处巡查,∠BCD=60°.在救生员甲从A处向D处跑的同时,乙从C处游向B处,已知乙在海水中的游泳速度也是2米/秒.请比较甲、乙两名救生员谁先到达B处.
在△ABC中,AB=6,AC=5,点D在边AB上,且AD=2,点E在边AC上,当AE=时,以A,D,E为顶点的三角形与△ABC相似.
最近更新
- “战士双脚走天下,四渡赤水出奇兵。乌江天险重飞渡,兵临贵阳逼昆明……”歌曲《四渡赤水出奇兵》描绘了红军长征的壮美画卷。
- 第二节:书面表达(满分25分)你的朋友李华是高中毕业生。他对填报志愿时是首先考虑专业还是学校拿不定主意。他想了解你们学校
- 随着经济的发展,文化越来越渗透进人们的日常生活中。如吃饭讲求“饮食文化”,穿衣讲求“服饰文化”,住房讲求“建筑文化”,上
- 公共汽车上涉及到许多物理知识,其中分析正确的是 A.轮胎上有花纹——用来减小摩擦 B.使用的I
- 下图是几种元素的原子结构示意图,请根据题目要求填写下列空白 (1) 属于金属元素的是 ,其原子结构特点为
- 下列动植物①金丝猴 ②斑马 ③扬子鳄 ④朱鹮 ⑤珙桐 ⑥银杉⑦美洲狮 ⑧水葫芦 中是我国特有的是 ( ) A. ①
- 反应X(g)+3Y(g)2Z(g);ΔH<0 在不同温度、不同压强(P1>P2)下,达到平衡时,混合气体中Z的体积分数φ
- Many people like to travel by plane, but I don't like it
- 已知实系数一元二次方程的两个实根为且则的取值范围是 ( ) A. B. C
- ......
- ____ by his teachers, he felt nervous. A. Having watched
- 2010年1月25日,国家质检总局局长王勇与广西壮族自治区主席马飚签署了《关于推动北部湾经济区开放开发,促进广西经济社会
- 若双曲线的离心率为2,则等于 A. 1 B. C. D.
- 高铁开通后,杭州到上海的动车改为31趟,最快一趟运行时间约1小时18分钟。把动力装置分散安装在每节车厢上,使其既具有牵引
- 阅读下面材料,根据要求作文。 曾国藩说:“天可补,海可填,南山可移。日月既往,不可复追。” 泰戈尔说:“如果错过了太阳时
- 中国东南部与阿拉伯半岛纬度大致相当,但并未出现沙漠,其主要原因是( )。 A .地势高,气温高 B.位于季风气候区
- 某混合气体,经分析只含碳、氧两种元素,且氧元素与碳元素的质量比大于8∶3。则混合气体的组成不可能是( ) A.CO2
- They have earned lots of money,soI________believe that the b
- 精子获能所利用的化学物质可以是 A.一定浓度的肝素 B.一定浓度的ATP C.一定浓度的葡萄糖 D.一定浓度的血清
- On a cold morning, I heard someone trying to get his car out



