九年级(初三)数学下学期下册试题
点A(﹣5,y1),B(3,y2)都在双曲线y=  ,则y1 , y2的大小关系是.
,则y1 , y2的大小关系是.
 ,则y1 , y2的大小关系是.
,则y1 , y2的大小关系是.
如图,立体图形的俯视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D .
如图,在  的正方形网格中,连结两格点A,B,点C、D是线段
的正方形网格中,连结两格点A,B,点C、D是线段  与网格线的交点,则
与网格线的交点,则  为
为 

 的正方形网格中,连结两格点A,B,点C、D是线段
的正方形网格中,连结两格点A,B,点C、D是线段  与网格线的交点,则
与网格线的交点,则  为
为 


A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在反比例函数 的每一条曲线上,y都随着x的增大而减小,则k的值可以是( )
的每一条曲线上,y都随着x的增大而减小,则k的值可以是( )
 的每一条曲线上,y都随着x的增大而减小,则k的值可以是( )
的每一条曲线上,y都随着x的增大而减小,则k的值可以是( )
A . -1
B . 1
C . 2
D . 3
如图,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡顶A处的俯角为15°,山脚处B的俯角为60°,已知该山坡的坡度i=1:  ,点P、H,B,C,A在同一个平面上,点HBC在同一条直线上,且PH⊥BC,则A到BC的距离为( )
,点P、H,B,C,A在同一个平面上,点HBC在同一条直线上,且PH⊥BC,则A到BC的距离为( )
 ,点P、H,B,C,A在同一个平面上,点HBC在同一条直线上,且PH⊥BC,则A到BC的距离为( )
,点P、H,B,C,A在同一个平面上,点HBC在同一条直线上,且PH⊥BC,则A到BC的距离为( )
A . 10  米
B . 15米
C . 20
米
B . 15米
C . 20  米
D . 30米
米
D . 30米
 米
B . 15米
C . 20
米
B . 15米
C . 20  米
D . 30米
米
D . 30米
在双曲线y=  的任一支上,y都随x的增大而增大,则k的值可以是( )
的任一支上,y都随x的增大而增大,则k的值可以是( )
 的任一支上,y都随x的增大而增大,则k的值可以是( )
的任一支上,y都随x的增大而增大,则k的值可以是( )
A . 2
B . 0
C . ﹣2
D . 1
计算
-
(1) ﹣14﹣

-
(2) 6tan230°﹣cos30°•tan60°﹣2sin45°+cos60°.
如图,下列条件不能判定△ABC与△ADE相似的是( )
A .  B . ∠B=∠ADE
C .
B . ∠B=∠ADE
C .  D . ∠C=∠AED
D . ∠C=∠AED
 B . ∠B=∠ADE
C .
B . ∠B=∠ADE
C .  D . ∠C=∠AED
D . ∠C=∠AED
先化简,再求代数式  的值,其中
的值,其中  .
.
 的值,其中
的值,其中  .
.
如图,在平面直角坐标系中,已知抛物线y=ax2+bx+8与x轴相交于A,B两点,与y轴相交于点C,OA=4,OB=2,点D是抛物线上一动点,且在y轴的左侧,连接AD,BC,AC,CD.

-
(1) 求抛物线的函数表达式;
-
(2) 已知直线y=kx+8与x轴相交于点M(点M与点B不重合),若以点M,C,O为顶点的△MCO与△BCO相似,求k的值;
-
(3) 连接OD,若△DAC的面积是△ABC的面积的
 时,求△CDO的面积.
时,求△CDO的面积.
如图所给的三视图表示的几何体是( )

A . 长方体
B . 圆柱
C . 圆锥
D . 圆台
如图,n个边长为1的相邻正方形的一边均在同一直线上,点M1 , M2 , M3 , …Mn分别为边B1B2 , B2B3 , B3B4 , …,BnBn+1的中点,△B1C1M1的面积为S1 , △B2C2M2的面积为S2 , …△BnCnMn的面积为Sn , 则Sn=.(用含n的式子表示)

已知反比例函数 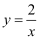 ,当
,当 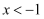 时,y的取值范围为.
时,y的取值范围为.
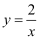 ,当
,当 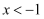 时,y的取值范围为.
时,y的取值范围为.
一段斜坡路面的截面图如图所示,BC⊥AC,其中坡面AB的坡比i1=1:2,现计划削坡放缓,新坡面的坡角为原坡面坡脚的一半,求新坡面AD的坡比i2(结果保留根号)

已知∠A是锐角,且sinA= , 那么锐角A的取值范围是( )
, 那么锐角A的取值范围是( )
 , 那么锐角A的取值范围是( )
, 那么锐角A的取值范围是( )
A . 0°<∠A<30°
B . 30°<∠A<45°
C . 45°<∠A<60°
D . 60°<∠A<90°
如图,一次函数y=k1x+b与反比例函数y=  的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
 的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5. 
-
(1) 求一次函数与反比例函数的解析式.
-
(2) 根据所给条件,请直接写出不等式k1x+b>
 的解集;
的解集;
-
(3) 若P(p,y1),Q(﹣2,y2)是函数y=
 图象上的两点,且y1≥y2 , 求实数p的取值范围.
图象上的两点,且y1≥y2 , 求实数p的取值范围.
如图,是将正方体切去一块后的几何体,则它的俯视图是( ).
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如果反比例函数y=  的图象经过点(﹣1,﹣2),则k的值是( )
的图象经过点(﹣1,﹣2),则k的值是( )
 的图象经过点(﹣1,﹣2),则k的值是( )
的图象经过点(﹣1,﹣2),则k的值是( )
A . 4
B . 0
C . ﹣3
D . ﹣4
下列水平放置的几何体中,俯视图是矩形的为( )
A . 圆柱  B . 长方体
B . 长方体  C . 三棱柱
C . 三棱柱  D . 圆锥
D . 圆锥 
 B . 长方体
B . 长方体  C . 三棱柱
C . 三棱柱  D . 圆锥
D . 圆锥 
如图所示,在山脚C处测得山项A仰角为30°,沿着水平地面向前300米到达点D,在D点测得山顶A的仰角为60°,则山高AB为米(结果保留根号).

最近更新
- One day something went wrong with a man’s bicycle chain(链条).
- 下列叙述不正确的是( )A.铅笔芯的主要成分不是铅,而是石墨B.化学创造了一个“新的自然界”C.向燃料中加入生石灰
- —What do you think ofHarry Potter and the Philosopher’s Ston
- 如图,AM‖CN,∠1=∠2,那么AB与CD平行吗?试说明理由.
- 下列反应能用离子方程式 CO32-+2H+=CO2↑+H2O表示的是 A. Na2CO3+2CH3COOH=2CH3CO
- Welcome to theElectronic Village to explore new ways of lang
- 是定义在上的函数 (1)判断函数的奇偶性; (2)利用函数单调性的定义证明:是其定义域上的增函数.
- —_____ Mr Smith ____ this week? — No. He is on holiday. A. H
- 下面的活动中,属于实践活动的是( ) A.蜜蜂酿蜜B.提高人们的思想觉悟C.人们认识世界和改造世界的能力与活动
- (三)名句默写(5分) 16.补写出下列句子中的空缺部分。(5分) ⑴韩愈在《师说》中说:从师与年纪无关,比自己年纪大的
- 如图所示,一平行金属板AB与一线圈组成一理想的LC振荡电路,E为电源,当开关K从1倒向2的同时有一电子恰从中央线飞入AB
- 我们学习过常见气体的实验室制法,知道了制取气体的一般思路和方法。 (1)实验室可用右图装置制取甲烷(CH4)气体,
- 下列电子式正确的是A.H2O2 B.CCl4C.MgCl2 D.NaOH
- 作为人体细胞的主要成分之一,约占体重的60%—70%,这种重要物质是 A. 蛋白质 B. 糖类 C
- 近代中国学习西方的“器物”到学习其制度,主要是由于( ) A.民族危机日益加深 B.国内阶级矛盾激化
- 右图是一定体积的氢气和不同体积的氧气化合成水(液态)的实验数据的关系图(横坐标表示反应前氧气的体积,纵坐标表示反应后剩余
- 下列地形区位于北美洲的是: A.巴西高原
- 直线x-2y-2k=0与2x-3y-k=0的交点在圆x2+y2=25上,则k的值是_____.
- 非诺洛芬是一种治疗类风湿性关节炎的药物,可通过以下方法合成:请回答下列问题: (1)非诺洛芬中的含氧官能团为______
- 经济全球化实质是以发达资本主义国家为主导的。广大发展中国家要参与全球化,就要遵守发达国家已制定好的“游戏规则”。这说明(



