九年级(初三)数学下学期下册试题
计算:  =.
=.
 =.
=.
已知反比例函数y= 的图象,在第一象限内y随x的增大而减小,则n的取值范围是 .
的图象,在第一象限内y随x的增大而减小,则n的取值范围是 .
 的图象,在第一象限内y随x的增大而减小,则n的取值范围是 .
的图象,在第一象限内y随x的增大而减小,则n的取值范围是 .
如图(1)是一种简易台灯,在其结构图(2)中灯座为△ABC(BC伸出部分不计),A、C、D在同一直线上.量得∠ACB=90°,∠A=60°,AB=16cm,∠ADE=150°,灯杆CD长为40cm,灯管DE长为16cm.

-
(1) 求DE与水平桌面(AB所在直线)所成的角;
-
(2) 求台灯的高(点E到桌面的距离).
如图是由几个相同的小立方体组成的左视图和俯视图,小立方块的个数最少是 .

小明尝试用自己所学的知识检测车速,如图,他将观测点设在到公路l的距离为0.1千米的P处.一辆轿车匀速直线行驶过程中,小明测得此车从A处行驶到B处所用的时间为4秒,并测得∠APO=59°,∠BPO=45°.根据以上的测量数据,请求出该轿车在这4秒内的行驶速度.(参考数据:sin59°≈0.86,cos59°≈0.52,tan59°≈1.66)

如图,AB和DE是直立在地面上的两根立柱.AB=4m,某一时刻AB在阳光下的投影BC=3m.

-
(1) 请你在图中画出此时DE在阳光下的投影.
-
(2) 在测量AB的投影时,同时测量出DE在阳光下的投影长为8m,请你计算DE的长.
一次函数y=kx+k(k≠0)和反比例函数  在同一直角坐标系中的图象大致是( )
在同一直角坐标系中的图象大致是( )
 在同一直角坐标系中的图象大致是( )
在同一直角坐标系中的图象大致是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在直角ΔABC中,已知∠C=90°,  ,求cosA=( )
,求cosA=( )
 ,求cosA=( )
,求cosA=( )
A . 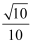 B .
B . 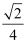 C .
C .  D .
D . 
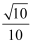 B .
B . 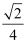 C .
C .  D .
D . 
已知  △
△  ,
,  和
和  是它们的对应中线,若
是它们的对应中线,若  ,
,  ,则
,则  与△
与△  的面积比等于等于.
的面积比等于等于.
 △
△  ,
,  和
和  是它们的对应中线,若
是它们的对应中线,若  ,
,  ,则
,则  与△
与△  的面积比等于等于.
的面积比等于等于.
如图,一扇窗户打开后可以用窗钩  将其固定,窗钩的一个端点
将其固定,窗钩的一个端点  固定在窗户底边
固定在窗户底边  上,且与转轴底端
上,且与转轴底端  之间的距离为20cm,窗钩的另一个端点
之间的距离为20cm,窗钩的另一个端点  在窗框边上的滑槽
在窗框边上的滑槽  上移动,滑槽
上移动,滑槽  的长度为17cm,
的长度为17cm,  、
、 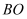 、
、 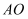 构成一个三角形.当窗钩端点
构成一个三角形.当窗钩端点  与点
与点  之间的距离是7cm的位置时(如图2),窗户打开的角
之间的距离是7cm的位置时(如图2),窗户打开的角 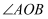 的度数为
的度数为 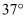 .求窗钩
.求窗钩  的长度(精确到1cm).(参考数据:
的长度(精确到1cm).(参考数据:  ,
, 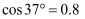 ,
,  )
)
 将其固定,窗钩的一个端点
将其固定,窗钩的一个端点  固定在窗户底边
固定在窗户底边  上,且与转轴底端
上,且与转轴底端  之间的距离为20cm,窗钩的另一个端点
之间的距离为20cm,窗钩的另一个端点  在窗框边上的滑槽
在窗框边上的滑槽  上移动,滑槽
上移动,滑槽  的长度为17cm,
的长度为17cm,  、
、 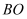 、
、 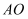 构成一个三角形.当窗钩端点
构成一个三角形.当窗钩端点  与点
与点  之间的距离是7cm的位置时(如图2),窗户打开的角
之间的距离是7cm的位置时(如图2),窗户打开的角 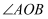 的度数为
的度数为 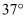 .求窗钩
.求窗钩  的长度(精确到1cm).(参考数据:
的长度(精确到1cm).(参考数据:  ,
, 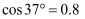 ,
,  )
) 
计算: .
.
 .
.
如图,将一副直角三角板拼放在一起得到四边形ABCD,其中∠BAC=45°,∠ACD=30°,点E为CD边上中点,连接AE,将△ADE沿AE所在直线翻折得到△  ,
,  交AC于F点,若AB=6
交AC于F点,若AB=6  .
.
 ,
,  交AC于F点,若AB=6
交AC于F点,若AB=6  .
. 
-
(1) 求CD的长;
-
(2) 求证:
 ;
;
-
(3) 设点P是线段上异于A、C的一动点,点P在何处时,DP+EP的值最小,并求出这个最小值.
如图,杂技团进行杂技表演,一名演员从跷跷板右端A处恰好弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线  的一部分,跳起的演员距点A所在y轴的水平距离为2.5米时身体离地面最高.若人梯到起跳点A的水平距离为4米,则人梯BC的高为米.
的一部分,跳起的演员距点A所在y轴的水平距离为2.5米时身体离地面最高.若人梯到起跳点A的水平距离为4米,则人梯BC的高为米.
 的一部分,跳起的演员距点A所在y轴的水平距离为2.5米时身体离地面最高.若人梯到起跳点A的水平距离为4米,则人梯BC的高为米.
的一部分,跳起的演员距点A所在y轴的水平距离为2.5米时身体离地面最高.若人梯到起跳点A的水平距离为4米,则人梯BC的高为米. 
设点O为投影中心,长度为1的线段AB平行于它在面H内的投影A′B′,投影A′B′的长度为3,且O到直线AB的距离为1.5,那么直线AB与直线A′B′的距离为 .

某商品的外包装盒的三视图如图所示,则这个包装盒的侧面积为( )

A . 150πcm2
B . 200πcm2
C . 300πcm2
D . 400πcm2
在Rt△ABC中,∠C=90°,tanA= 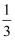 ,则cosB的值为( )
,则cosB的值为( )
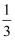 ,则cosB的值为( )
,则cosB的值为( )
A .  B .
B .  C .
C . 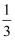 D .
D . 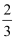
 B .
B .  C .
C . 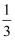 D .
D . 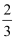
如图,图①是某电脑液晶显示器的侧面图,显示屏AO可以绕点O旋转一定的角度.研究表明:显示屏顶端A与底座B的连线AB与水平线BC垂直时(如图②),人观看屏幕最舒适.此时测得∠BAO=15°,AO=30cm,∠OBC=45°,求AB的长度.(结果精确到1cm)(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,  ≈1.414)
≈1.414)
 ≈1.414)
≈1.414) 
已知⊙O的直径AB=2,过点A的两条弦AC= , AD=
, AD= , 则∠CBD=
, 则∠CBD=
 , AD=
, AD= , 则∠CBD=
, 则∠CBD=
如图,已知  ,相似比为
,相似比为  ,且
,且  的三边长分别为a、b、c
的三边长分别为a、b、c  ,
,  的三边长分别为
的三边长分别为  、
、 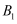 、
、  .
.
 ,相似比为
,相似比为  ,且
,且  的三边长分别为a、b、c
的三边长分别为a、b、c  ,
,  的三边长分别为
的三边长分别为  、
、 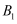 、
、  .
. 
-
(1) 若
 ,求证:
,求证:  ;
;
-
(2) 若
 ,试给出符合条件的一对
,试给出符合条件的一对  和
和  ,使得a、b、c和
,使得a、b、c和  、
、 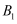 、
、  .都是正整数,并加以说明;
.都是正整数,并加以说明;
-
(3) 若
 ,
,  ,是否存在
,是否存在  和
和  使得
使得  ?请说明理由.
?请说明理由.
函数y=  的大致图象为( )
的大致图象为( )
 的大致图象为( )
的大致图象为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
最近更新
- 对于密闭容器中进行的反应N2+O22NO,下列条件能加快其反应速率的是 A.增大体积使压强减小 B.
- 阅读下面的文字,根据要求作文。 犹太经典著作《塔木德》中有一句话:和狼生活在一起,你只能学会嚎叫;和那些优秀的人接触,你
- 材料一:2010年中国上海世博会以“城市,让生活更美好”为主题。它所包含的五个分主题:城市与经济发展关系、城市与可持续发
- 下列词语中,表示气候的是 ( )①风雨交加 ②风和日丽 ③冬冷夏热
- 19世纪中期欧洲有个出版社想出版法国作家巴尔扎克的小说集《人间喜剧》。为吸引读者,出版社想为小说配一些插图,插图的风格要
- 阅读下列材料“秦王扫六合,虎视何雄哉!挥剑决浮云,诸侯尽西来。”——李白“祖舜宗尧自太平,秦皇何事苦苍生。不知祸起萧墙内
- 五四运动前后,通过发表文章,比较全面地介绍了马克思主义,在传播马克思主义方面起了重要作用的是 A.梁启超
- 为应对国际金融危机,国家采取了一系列促进房地产市场健康发展的政策。这些政策对于提振信心、活跃市场、促进住房消费和投资,实
- 温度计是根据液体的 规律制成。我们实验时,测量的沸水温度值往往低于100℃,原因是实验室气压
- 阅读下面的文字,完成1-3题。真实的沃伦·巴菲特[美]詹姆斯·奥洛克林①资本市场为&ldqu
- 下列关于酶的叙述,不正确的是( ) A.酶是活细胞产生的一类具有生物催化作用的有机物 B.酶的催化作用具有专一性和
- 依次填入下面一段文字横线处的语句,与上下文衔接最恰当的一组是( ) 发射时间定在凌晨。___________。火箭_
- 一台笔记本电脑标价125000元一台,在这里体现的货币职能是 A.价值尺度 B.流通手段
- 某同学家里有一个“,”的小灯泡。 ①该同学使用多用电表粗略测量小灯泡不工作时的电阻。请你根据实验要求,完成下列实验步骤。
- —Have you finished your composition already, Jack? —Yes, I _
- 下列可逆反应达到平衡时,增大压强和升高温度使平衡移动方向相同的是( ) A.NH4HCO3(s)NH3(g)+H2
- .我国下列省级行政区中,有两个简称的是( ) A.湖北、湖南 B.西藏、台湾 C.山西、
- 生活中包含着许多化学知识,对下列做法的解释不合理的是A.铁栏杆上涂铝粉——铝的化学性质没有铁活泼 B.食品袋内充入氮气—
- 已知函数的一部分图象如下图所示,如果,则( ) A. B. C. D.
- 如右图,在等腰梯形ABCD中,AD∥BC,AD=AB.过A作AF⊥BD,交BC于G,延长BC至E,使CE=CD.1.(



