九年级(初三)数学下学期下册试题
已知圆锥的母线长为5cm,高为4cm,则该圆锥的侧面积为cm2(结果保留π)

如图,矩形ABCD中,AB=15,BC=9,E是CD边上一点(不与点C重合),作AF⊥BE于F,CG⊥BE于G,延长CG至点C′,使C′G=CG,连接CF,AC′.

-
(1) 直接写出图中与△AFB相似的一个三角形;
-
(2) 若四边形AFCC′是平行四边形,求CE的长;
-
(3) 当CE的长为多少时,以C′,F,B为顶点的三角形是以C′F为腰的等腰三角形?
若sinA=  ,则cos(90°﹣A)=.
,则cos(90°﹣A)=.
 ,则cos(90°﹣A)=.
,则cos(90°﹣A)=.
为了学生的安全,某校决定把一段如图所示的步梯路段进行改造.已知四边形  为矩形,
为矩形,  ,其坡度为
,其坡度为  ,将步梯
,将步梯  改造为斜坡
改造为斜坡 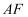 ,其坡度为
,其坡度为  ,求斜坡
,求斜坡 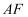 的长度.(结果精确到
的长度.(结果精确到  ,参考数据:
,参考数据:  ,
,  )
)
 为矩形,
为矩形,  ,其坡度为
,其坡度为  ,将步梯
,将步梯  改造为斜坡
改造为斜坡 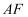 ,其坡度为
,其坡度为  ,求斜坡
,求斜坡 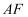 的长度.(结果精确到
的长度.(结果精确到  ,参考数据:
,参考数据:  ,
,  )
) 
如图,已知  是双曲线
是双曲线  上一点,过点
上一点,过点  作
作  轴,交双曲线
轴,交双曲线  于点
于点  ,过点
,过点  作
作  交
交  轴于点
轴于点  .连接
.连接  ,则
,则  的面积为.
的面积为.
 是双曲线
是双曲线  上一点,过点
上一点,过点  作
作  轴,交双曲线
轴,交双曲线  于点
于点  ,过点
,过点  作
作  交
交  轴于点
轴于点  .连接
.连接  ,则
,则  的面积为.
的面积为. 
如图,G是△ABC的中位线MN的中点,CG的延长线交AB于点F , 则AF:FB等于( )

A . 1:2
B . 1:3
C . 2:3
D . 3:4
如图,在△ABC中,CD⊥AB,∠ACD=45°,∠DCB=60°,CD=40,求AB.

某品牌热水器中原有水的温度为20℃,开机通电,热水器启动开始加热(此过程中水温y℃与开机时间x分钟满足一次函数关系),当加热到70℃时自动停止加热,随后水温开始下降(此时水温y℃与开机时间x分钟成反比例函数关系).当水温降至35℃时,热水器又自动以相同的功率加热至70℃,…,重复上述过程.如图,根据图象提供的信息,解答下列问题:

-
(1) 当0≤x≤25时,求水温y℃开机时间x分钟的函数表达式;
-
(2) 求图中t的值;
-
(3) 开机通电60分钟时,热水器中水的温度y约为多少摄氏度?
若反比例函数y=  的图象经过点(﹣1,﹣2),则k的值为( )
的图象经过点(﹣1,﹣2),则k的值为( )
 的图象经过点(﹣1,﹣2),则k的值为( )
的图象经过点(﹣1,﹣2),则k的值为( )
A . ﹣2
B . ﹣1
C . 1
D . 2
如图,在平面直角坐标系中,已知  中点
中点  的坐标为(4,2),以坐标原点
的坐标为(4,2),以坐标原点  为位似中心,在第三象限内,将
为位似中心,在第三象限内,将  边长放大2倍得到了
边长放大2倍得到了  ,则点
,则点  对应点
对应点  的坐标为( )
的坐标为( )
 中点
中点  的坐标为(4,2),以坐标原点
的坐标为(4,2),以坐标原点  为位似中心,在第三象限内,将
为位似中心,在第三象限内,将  边长放大2倍得到了
边长放大2倍得到了  ,则点
,则点  对应点
对应点  的坐标为( )
的坐标为( ) 
A . ( 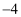 ,
,  )
B . (
)
B . (  ,
, 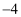 )
C . (
)
C . ( 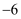 ,
, 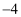 )
D . (8,4)
)
D . (8,4)
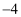 ,
,  )
B . (
)
B . (  ,
, 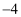 )
C . (
)
C . ( 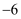 ,
, 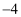 )
D . (8,4)
)
D . (8,4)
如图1,2分别是某款篮球架的实物图与示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HF与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米).
(参考数据:cos75°≈0.2588, sin75°≈0.9659,tan75°≈3.732,  ,
,  )
)


如图,点  是正方形
是正方形  内一点,
内一点,  是等边三角形,连接
是等边三角形,连接  对角线
对角线  交
交 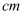 于点
于点  ,现有以下结论:①
,现有以下结论:①  ;②
;②  ;③
;③  ;④
;④  ,其中正确的结论有( )
,其中正确的结论有( )
 是正方形
是正方形  内一点,
内一点,  是等边三角形,连接
是等边三角形,连接  对角线
对角线  交
交 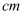 于点
于点  ,现有以下结论:①
,现有以下结论:①  ;②
;②  ;③
;③  ;④
;④  ,其中正确的结论有( )
,其中正确的结论有( ) 
A . 1
B . 2
C . 3
D . 4
如图摆放的下列几何体中,左视图是圆的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,平面直角坐标系中,点A是x轴上任意一点,BC平行于x轴,分别交y=  (x>0)、y=
(x>0)、y=  (x<0)的图象于B,C两点,若△ABC的面积为2,则k值为( )
(x<0)的图象于B,C两点,若△ABC的面积为2,则k值为( )
 (x>0)、y=
(x>0)、y=  (x<0)的图象于B,C两点,若△ABC的面积为2,则k值为( )
(x<0)的图象于B,C两点,若△ABC的面积为2,则k值为( ) 
A . ﹣1
B . 1
C .  D .
D . 
 D .
D . 
如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为45°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为110米,那么该建筑物的高度BC约为多少米?(结果保留整数,  ≈1.73)
≈1.73)
 ≈1.73)
≈1.73) 
某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端,测得仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米)
(参考数据:sin48°≈ 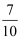 ,tan48°≈
,tan48°≈ 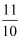 ,sin64°≈
,sin64°≈ 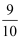 ,tan64°≈2)
,tan64°≈2)

函数y=x+m与 
 在同一坐标系内的图象可以是( )
在同一坐标系内的图象可以是( )

 在同一坐标系内的图象可以是( )
在同一坐标系内的图象可以是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,海面上产生了一股强台风.台风中心A在某沿海城市B的正西方向,小岛C位于城市B北偏东29°方向上,台风中心沿北偏东60°方向向小岛C移动,此时台合风中心距离小岛200海里.

-
(1) 过点B作
 于点P,求
于点P,求 的度数;
的度数;
-
(2) 据监测,在距离台风中心50海里范围内均会受到台风影响(假设台风在移动过程中风力保持不变).问:在台风移动过程中,沿海城市B是否会受到台风影响?请说明理由.(参考数:
 ,
,  ,
,  ,
,  )
)
如图四个几何体:其中从左面看到的形状图与从上面看到的形状图相同的几何体共有( )

A . 1个
B . 2个
C . 3个
D . 4个
如图,小丽在观察某建筑物AB.
(1)请你根据小亮在阳光下的投影,画出建筑物AB在阳光下的投影.
(2)已知小丽的身高为1.65m,在同一时刻测得小丽和建筑物AB的投影长分别为1.2m和8m,求建筑物AB的高.
最近更新
- 下列实验操作中正确的是 A.取用少量液体 B.过滤 C.闻气味 D.稀释浓硫
- 阅读下面的文字,完成7―10题。文化是庞大的集合体,可以有不同的划分标准。按社区分,中国传统文化分乡镇文化、山林文化、江
- (02年北京卷)下面是5月21日某报刊发的一则消息,请概括主要信息。(不超过60字)(3分) 5月27至28日,“
- 瑞瑞同学有一辆玩具电动车,在行驶的过程中,车上的小动物可以自由旋转,这种功能是由两个电动机带动的. 如图所示是该玩具电动
- 300 mL某浓度的NaOH溶液中含有60 g溶质。现欲配制1 mol/L的NaOH溶液,应取原溶液与蒸馏水的体积比约为
- 阅读下面的文言文,完成后面小题。 契苾何力,九岁而孤。贞观六年,与母率众千余诣沙州内属,太宗处其部于甘、凉二州,擢何力左
- 下图甲为我国建立的三个南极科考站。中山站 (69º22′S,76º22′E),长城站(62º12′S,58º57′W)
- 我们把焦点相同,且离心率互为倒数的椭圆和双曲线称为一对“相关曲线”.已知F1、F2是一对相关曲线的焦点,P是它们在第一象
- ________you don’t like him is none of my business. A. What
- 下列关于碱金属的电子结构和性质的叙述中不正确的是() A. 碱金属原子最外层都只有一个电子,在化学反应中容易失去
- 在宏观、微观和符号之间建立联系是化学学科的特点. 甲、乙、丙、丁表示四种物质,它们的部分化学式和微观示意图分别列于下表.
- 辘辘远听,____________ 。 (杜牧《阿房宫赋》)
- There____ some meat in the fridge, so you don’t need to buy
- 近年来,桂林开展了“绿色出行”(GreenTransportation)计划,向市民提供了大批量的公共自行车。学校将举办
- 如图,在平面直角坐标系中,二次函数y=ax2+mc(a≠0)的图像经过正方形ABOC的三个顶点,且ac=-2,则m的值为
- 袋子A和B中装有若干个均匀的红球和白球,从A中摸出一个红球的概率是,从B中摸出一个红球的概率为p. (Ⅰ) 从A中有
- 读“珠三角地区产业转移圈层示意图”,完成8-9题。8.珠江三角洲地区部分产业转移出去的主要原因不包括A.当地人口稠密、交
- 梭伦在诗中解释了他的目标。他谈到“euno-mia”或者说“好的政府”,把这解释为平衡公民互相冲突的利益。后来的哲学家叔
- 据报道:“目前世界上有近20亿人患有缺铁性贫血”,这里的“铁”是指( ) A铁元素 B.四氧化三铁
- 某研究性学中发病率很高。通过对该家庭中一对夫妇及其子女的调查,画出了遗传图谱。据图可以做出的判断是A.母亲肯定是纯合子,



