九年级(初三)数学下学期下册试题
如图,在第一象限内有一点A(4,1),过点A作AB⊥x轴于B点,作AC⊥y轴于C点,点N为线段AB上的一动点,过点N的反比例函数y=  交线段AC于M点,连接OM,ON,MN.
交线段AC于M点,连接OM,ON,MN.
 交线段AC于M点,连接OM,ON,MN.
交线段AC于M点,连接OM,ON,MN. 
-
(1) 若点N为AB的中点,则n的值为;
-
(2) 求线段AN的长(用含n的代数式表示);
-
(3) 求△AMN的面积等于
 时n的值.
时n的值.
如图不能折叠成正方体的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
下列几何体的主视图、俯视图和左视图都是长方形的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  D .
D . 
对于下图所示的几何体,正确的俯视图是()

A .  B .
B .  C .
C .  D .
D . 
如图,在△ABC中,EF∥BC,  =
=  ,S四边形BCFE=8,则S△ABC=( )
,S四边形BCFE=8,则S△ABC=( )
 =
=  ,S四边形BCFE=8,则S△ABC=( )
,S四边形BCFE=8,则S△ABC=( ) 
A . 9
B . 10
C . 12
D . 13
与图中的三角形相似的是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知线段a、b、c,其中c的长度是a、b长度的比例中项,若a=9cm,b=4cm,则线段c的长为( )
A . 5cm
B . 6cm
C . 18cm
D . ±6cm
计算:
-
(1) 2(x+1)2﹣8=0;
-
(2) 3x2﹣5x+1=0;
-
(3)
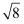 +2cos60°﹣4sin45°;
+2cos60°﹣4sin45°;
-
(4) 2﹣1﹣tan60°+(
 ﹣1)0+|1﹣
﹣1)0+|1﹣  |
|
如图,在  中,已知
中,已知  ,则下列等式成立的是
,则下列等式成立的是 

 中,已知
中,已知  ,则下列等式成立的是
,则下列等式成立的是 


A . 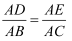 B .
B .  C .
C .  D .
D . 
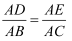 B .
B .  C .
C .  D .
D . 
已知a、b、c、d是成比例线段,即 =
= , 其中a=3cm,b=2cm,c=6cm,则线段d= cm .
, 其中a=3cm,b=2cm,c=6cm,则线段d= cm .
 =
= , 其中a=3cm,b=2cm,c=6cm,则线段d= cm .
, 其中a=3cm,b=2cm,c=6cm,则线段d= cm .
某市政府计划建设一项水利工程,工程需要运送的土石方总量为 立方米,某运输公司承担了运送土石方的任务.
立方米,某运输公司承担了运送土石方的任务.
 立方米,某运输公司承担了运送土石方的任务.
立方米,某运输公司承担了运送土石方的任务.
-
(1) 设该公司平均每天运送土石方总量为
 立方米,完成运送任务所需时间为
立方米,完成运送任务所需时间为 天.
天.①求
 关于
关于 的函数表达式.
的函数表达式.②若
 时,求
时,求 的取值范围.
的取值范围. -
(2) 若1辆卡车每天可运送土石方
 立方米,工期要求在80天内完成,公司至少要安排多少辆相同型号卡车运输?
立方米,工期要求在80天内完成,公司至少要安排多少辆相同型号卡车运输?
为倡导“低碳生活”,常选择以自行车作为代步工具.如图1所示是一辆自行车的实物图,车架档AC与CD的长分别为45cm,60cm,且它们互相垂直,座杆CE的长为20cm,车轮半径28cm,点A,C,E在同一条直线上,且∠CAB=75°,如图2

-
(1) 求车座点E到地面的距离;(结果精确到1cm)
-
(2) 求车把点D到车架档直线AB的距离.(结果精确到1cm).
两个相似三角形的面积比等于4:9,则它们对应边上的高之比等于.
已知:直角三角形的铁片ABC的两条直角边BC、AC的长分别为6和8,如图所示,分别采用(1)(2)两种方法,剪出一块正方形铁片,为使剪去正方形铁片后剩下的边角料较少,试比较哪种剪法较为合理,并说明理由.

由5个大小相同的小正方体拼成的几何体如图所示,则下列说法正确的是( )

A . 主视图的面积最小
B . 左视图的面积最小
C . 俯视图的面积最小
D . 三个视图的面积相等
已知,如图,在平面直角坐标系中,正方形ABCD,点A(0,10),点B(8,4),点C在第一象限,点P从顶点A出发,沿着正方形的边长逆时针运动一周,在OP右侧作∠OPQ=∠OAB交x轴于点Q.

-
(1) 求点C坐标.
-
(2) 当点P与点B重合时,求OQ的长.
-
(3) 在点P的整个运动过程中,当△OPQ是以PQ为腰的等腰三角形时,求OQ的长.
如图,在矩形  中,
中,  是
是  边的中点,
边的中点,  与
与  垂直,交
垂直,交  于点
于点  ,连接
,连接  ,则下列结论错误的是( )
,则下列结论错误的是( )
 中,
中,  是
是  边的中点,
边的中点,  与
与  垂直,交
垂直,交  于点
于点  ,连接
,连接  ,则下列结论错误的是( )
,则下列结论错误的是( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在 中,弦
中,弦 的长为
的长为 , 圆心到弦
, 圆心到弦 的距离为6,则
的距离为6,则 的度数为.
的度数为.
 中,弦
中,弦 的长为
的长为 , 圆心到弦
, 圆心到弦 的距离为6,则
的距离为6,则 的度数为.
的度数为.

反比例函数  的图象经过点A(﹣1,3),则k的值为( )
的图象经过点A(﹣1,3),则k的值为( )
 的图象经过点A(﹣1,3),则k的值为( )
的图象经过点A(﹣1,3),则k的值为( )
A . k=3
B . k=﹣3
C . k=6
D . k=﹣6
如果反比例函数y=  的图象经过点(﹣5,3),则k=( )
的图象经过点(﹣5,3),则k=( )
 的图象经过点(﹣5,3),则k=( )
的图象经过点(﹣5,3),则k=( )
A . 15
B . ﹣15
C . 16
D . ﹣16
最近更新
- 一打点计时器固定在倾角为θ的斜面上,一小车拖着穿过打点计时器的纸带从斜面上滑下,打出的纸带的一段如图所示.纸带上0、1、
- 2009年2月12日是伟大科学家达尔文诞生诞辰200周年,同时也是其《物种起源》出版150周年,全世界的纪念活动悄然兴起
- 2009年新中国60周年华诞,首都北京见证了新中国诞生与发展的历史依据所学知识回答下列问题。 (1)二十世纪四十年代末和
- 一个四面的所有棱长都为,四个顶点在同一球面上,则此球的表面积为 .
- 下列动物中用气囊辅助肺进行呼吸的是( )A.丹顶鹤 B.青蛙 C.扬子鳄 D
- .(10年云南玉溪15)下图是元素周期表中提供的硫元素的相关信息,对图中信息理解错误的是( )A.该元素原子的最外
- 某同学书写的试剂标签如下图所示,其中错误的是
- 已知是上的减函数,那么的取值范围是 ( ). A. B. C. D.
- 当人看到酸梅时唾液分泌会大量增加,对此现象的分析,错误的是() A. 这是一种反射活动,唾液腺的分泌物不属
- 已知双曲线=1的右焦点是F,右顶点是A,虚轴的上端点是B,·=6-4,∠BAF=150°. (1)求双曲线的方程; (2
- 阅读下面的文言文,完成文后各题。 横渠先生行状 【宋】吕大临 先生讳载,字子厚,世大梁人。少孤自立,无所不学。与焦寅游,
- 2011年6月27日,中国社科院发布《中国政治参与报告 (2011)》,可视为第二本国 家权威机构发布的中国公民政治
- 以下说法中正确的是 A.阳光射入房间内看到尘土飞扬,可以说明分子做无规则运动 B.物体放出热量,其温度一定降低 C.固体
- 在探究凸透镜成像的实验中,当烛焰、凸透镜、光屏位于如图所示的位置时,烛焰在光屏上呈现一个清晰的缩小的像,要使烛焰在光屏上
- 我国古代四大发明中,涉及到电磁现象应用的发明是( )A.指南针 B.造纸术 C.印刷术 D.火
- 下列物质中,既含离子键又含共价键的是( ) A.Na2O B.NH3 C.Ca(OH
- 如图所示的电路中,电源电压保持不变.R1为滑动变阻器,R2、R3为定值电阻.闭合开关S,将滑片P由a端向b端滑动一段距离
- 日本宣布无条件投降的时间是l945年( ) A.8月15日 B.9月2日 C
- 下图为“祁连山冰川朝向玫瑰图”,它是把祁连山总的冰川条数和面积分成100份,把其中4份作为一个长度和面积单位,按不同的方
- —Is Jissica a diligent student ? —No , but she is a lazy



