九年级(初三)数学下学期下册试题
如图,线段OA与反比例函数y  在第一象限的图象相交于点B(4,3),点B是OA的中点,AC∥x轴交反比例函数的图象于点C.
在第一象限的图象相交于点B(4,3),点B是OA的中点,AC∥x轴交反比例函数的图象于点C.
 在第一象限的图象相交于点B(4,3),点B是OA的中点,AC∥x轴交反比例函数的图象于点C.
在第一象限的图象相交于点B(4,3),点B是OA的中点,AC∥x轴交反比例函数的图象于点C.

求:
-
(1) m的值;
-
(2) 求AC的长.
计算: 

先化简,再求代数式  的值,其中a=tan60°-6sin30°.
的值,其中a=tan60°-6sin30°.
 的值,其中a=tan60°-6sin30°.
的值,其中a=tan60°-6sin30°.
如图,在3×3正方形网格中,顶点是网格线的交点的三角形叫做格点三角形,给出下列命题:
①一定存在全等的两个格点三角形
②一定存在相似且不全等的两个格点三角形
③一定存在两个格点三角形是位似图形
④一定存在周长和面积均为无理数的格点三角形
其中真命题的个数是( )

A . 4个
B . 3个
C . 2个
D . 1个
如图是反比例函数y= 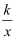 在第二象限内的图象,若图中的矩形OABC的面积为2,则k=
在第二象限内的图象,若图中的矩形OABC的面积为2,则k=
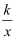 在第二象限内的图象,若图中的矩形OABC的面积为2,则k=
在第二象限内的图象,若图中的矩形OABC的面积为2,则k= 
如图所示的几何体的俯视图是( )

A .  B .
B .  C .
C .  D .
D . 
计算 +|﹣
+|﹣ |﹣(﹣2015)0+(
|﹣(﹣2015)0+( )﹣1﹣3tan60°.
)﹣1﹣3tan60°.
 +|﹣
+|﹣ |﹣(﹣2015)0+(
|﹣(﹣2015)0+( )﹣1﹣3tan60°.
)﹣1﹣3tan60°.
如图,在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a、b、c,我们把∠A的邻边与斜边的比叫做∠A的余弦,记作cosA,即cosA= . 当c=2,a=1时,求cosA.
. 当c=2,a=1时,求cosA.
 . 当c=2,a=1时,求cosA.
. 当c=2,a=1时,求cosA. 
在△ABC中,若∠A,∠B满足|sinA- |+(1-tanB)2=0,则∠C的度数是( )
|+(1-tanB)2=0,则∠C的度数是( )
 |+(1-tanB)2=0,则∠C的度数是( )
|+(1-tanB)2=0,则∠C的度数是( )
A . 45°
B . 60°
C . 75°
D . 105°
如图,以AB为直径作半圆O,点C是半圆上一点,∠ABC的平分线交⊙O于E,D为BE延长线上一点,且∠DAE=∠FAE.

-
(1) 求证:AD为⊙O切线;
-
(2) 若sin∠BAC=
 ,求tan∠AFO的值.
,求tan∠AFO的值.
已知反比例函数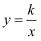 的图象经过点(a,b),则它的图象也一定经过( )
的图象经过点(a,b),则它的图象也一定经过( )
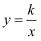 的图象经过点(a,b),则它的图象也一定经过( )
的图象经过点(a,b),则它的图象也一定经过( )
A . (-a,-b)
B . (a,-b)
C . (-a,b)
D . (0,0)
如图,在 中,
中,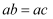 , 点D在
, 点D在 上(不与点A,C重合),只需添加一个条件即可证明
上(不与点A,C重合),只需添加一个条件即可证明 和
和 相似,这个条件可以是(写出一个即可).
相似,这个条件可以是(写出一个即可).
 中,
中,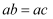 , 点D在
, 点D在 上(不与点A,C重合),只需添加一个条件即可证明
上(不与点A,C重合),只需添加一个条件即可证明 和
和 相似,这个条件可以是(写出一个即可).
相似,这个条件可以是(写出一个即可).
如图,点  是函数
是函数  图象上的一点,连接
图象上的一点,连接 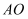 ,交函数
,交函数  的图象于点
的图象于点  ,点
,点  是
是  轴上的一点,且
轴上的一点,且  ,则
,则  的面积为.
的面积为.
 是函数
是函数  图象上的一点,连接
图象上的一点,连接 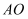 ,交函数
,交函数  的图象于点
的图象于点  ,点
,点  是
是  轴上的一点,且
轴上的一点,且  ,则
,则  的面积为.
的面积为. 
如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )

A . 美
B . 丽
C . 广
D . 安
已知反比例函数  的图像经过点
的图像经过点  ,那么
,那么  的值是.
的值是.
 的图像经过点
的图像经过点  ,那么
,那么  的值是.
的值是.如图,在平面直角坐标系中,点A(﹣6,0),点B(0,2 ),点P在第二象限内,若以点P、B、O为顶点的三角形与△AOB相似(不包括全等的情况),则点P的坐标为
),点P在第二象限内,若以点P、B、O为顶点的三角形与△AOB相似(不包括全等的情况),则点P的坐标为

如图,在同一时刻,测得小华和旗杆的影长分别为1m和6m,小华的身高约为1.6m,则旗杆的高约为m.

若双曲线 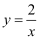 过两点(-1,y1),(-3,y2),则下列说法正确的是( )
过两点(-1,y1),(-3,y2),则下列说法正确的是( )
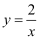 过两点(-1,y1),(-3,y2),则下列说法正确的是( )
过两点(-1,y1),(-3,y2),则下列说法正确的是( )
A . y1>y2
B . y1<y2
C . y1=y2
D . y1≥y2
如图1,等腰△ABC内接于⊙O,AC=BC,CD⊥AB于点D,F为弧AB上的一个动点,连接CF交AB于点G,P为射线AB上的一个动点,连接PF,AF.

-
(1) 求证:CF•CG=CA2;
-
(2) 如图1,若PG=PF,求证:PF为⊙O的切线;
-
(3) 在(2)的条件下,如图2,连接PC,若∠FAP=∠PCB,AB=CD=4,求
 的值.
的值.
关于反比例函数y=  ,下列说法不正确的是( )
,下列说法不正确的是( )
 ,下列说法不正确的是( )
,下列说法不正确的是( )
A . 函数图象分别位于第一、第三象限
B . 函数图象关于原点中心对称
C . 当x>0时,y随x的增大而增大
D . 当﹣8<x<﹣1时,﹣8<y<﹣1
最近更新
- 已知,,则( ) A. B. C. D.
- 2009年,我国实施较为宽松的汽车信贷政策,助推了汽车消费的增长。2010年,我国汽车产销量均突破1800万辆,位居世界
- 在Fe3O4 +4CO3Fe+4CO2的反应中,___________是氧化剂,____________是还原剂, __
- She is 13 years old and herbirthday is _____ September. A.in
- I began watching here an hour ago, butnow nothing________ y
- 二战后,美苏“冷战”开始的标志是 A.北大西洋公约组织建立 B.华沙条约组织建立 C.杜鲁门主义发表
- 某段铁路的长度为L的一根一根铁轨铺成的,如图5所示.一列火车匀速前进,车内一乘客欲测出火车运动的速度,他测得火车经铁轨缝
- 为了制定一个符合中国国情和时代特点的《国家中长期教育改革和发展规划纲要(2010——2020年)》(简称《纲要》),政府
- 最新的研究表明,一氧化氮吸入治疗法可以快速改善SARS重症患者的缺氧状况,缓解病情。病毒学研究同时证明,一氧化氮对SAR
- 我国不同主题的社区精神文明创建活动异彩纷呈:文明社区、绿色社区、平安社区、和谐社区、特色社区、精品社区、无毒社区、青年文
- ......
- Most of English learners want to know how the differences be
- 光合作用强度可以用多种指标表示,以下不适合的是 A.植物体鲜重增加量 B.植物体干重增加量
- 下图为“某月沿0°经线海平面平均气压分布图”。读图回答7~9题。 7.上述“某月”是A.1月 B.4月 C.7月
- 如图,▱ABCD的两条对角线AC,BD相交于点O. (1)图中有哪些三角形是全等的? (2)选出其中一对全等三角形进行证
- 在标准状况下,下列物质占体积最大的是()。 A. 18g H2O B.6.02×1023个氮分子
- 已知在促进生长的浓度范围内,浓度相同时,生长素类似物萘乙酸(NAA)产生的促进生长的作用大于吲哚乙酸(IAA)。为了验证
- 雅典的民主政治为人类提供了一种集体管理的新形式,它发挥了雅典公民的积极性,对经济文化的繁荣和国家的强盛起了积极作用。那么
- 根尖成熟区最明显的特点是 ( ) A.光滑呈乳白色
- Some fruit and vegetablesare________by chemical drugs.They l



