8 相似三角形的性质 知识点题库
如图,△ABC∽△A′B′C′,AB=3,A′B′=4.若S△ABC=18,则S△A′B′C′的值为( )
 B .
B .  C . 24
D . 32
C . 24
D . 32
如图1,点E为矩形ABCD边AD上一点,点P,点Q同时从点B出发,点P沿BE→ED→DC 运动到点C停止,点Q沿BC运动到点C停止,它们运动的速度都是1cm/s,设P,Q出发t秒时,△BPQ的面积为ycm2 , 已知y与t的函数关系的图形如图2(曲线OM为抛物线的一部分),则下列结论:①AD=BE=5cm;②当0<t≤5时, ;③直线NH的解析式为
;③直线NH的解析式为 ;④若△ABE与△QBP相似,则t=
;④若△ABE与△QBP相似,则t= 秒。其中正确的结论个数为( )
秒。其中正确的结论个数为( )
如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是.
①EF=  OE;②S四边形OEBF:S正方形ABCD=1:4;③BE+BF=
OE;②S四边形OEBF:S正方形ABCD=1:4;③BE+BF=  OA;④在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
OA;④在旋转过程中,当△BEF与△COF的面积之和最大时,AE=  ;⑤OG•BD=AE2+CF2 .
;⑤OG•BD=AE2+CF2 .

 的图象在第一象限内的交点为M,若△OBM的面积为1.
的图象在第一象限内的交点为M,若△OBM的面积为1.
-
(1) 求一次函数和反比例函数的表达式;
-
(2) 在x轴上是否存在点P,使AM⊥PM?若存在,求出点P的坐标;若不存在,说明理由;
-
(3) x轴上是否存在点Q,使△QBM∽△OAM?若存在,求出点Q的坐标;若不存在,说明理由.
-
(1)
如图1,若CE=CF,求证:DE=DF;

-
(2)
如图2,在∠EDF绕点D旋转的过程中:
①探究三条线段AB,CE,CF之间的数量关系,并说明理由;
②若CE=4,CF=2,求DN的长.

爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AM⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.

-
(1) 如图1,当tan∠PAB=1,c=4
 时,a=,b=;
时,a=,b=;如图2,当∠PAB=30°,c=2时,a=,b=;
-
(2) 请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
-
(3) 如图4,▱ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=3
 ,AB=3,求AF的长.
,AB=3,求AF的长.
 ,那么∠B的度数是( )
,那么∠B的度数是( )

 ,连接DE , 分别交BC , AC交于点F , G .
,连接DE , 分别交BC , AC交于点F , G . 
-
(1) 求证: BF=CF ;
-
(2) 若
 ,
,  ,求FG的长.
,求FG的长.

-
(1) 求抛物线的解析式.
-
(2) 若△AOC与△FEB相似,求a的值.
-
(3) 当PH=2时,求点P的坐标.

-
(1) 用含t的代数式表示线段DM的长度;
-
(2) 求当点Q落在BC边上时t的值;
-
(3) 设△PQM与△DEB重叠部分图形的面积为S(平方单位),当△PQM与△DEB有重叠且重叠部分图形是三角形时,求S与t的函数关系式;
-
(4) 当经过点C和△PQM中一个顶点的直线平分△PQM的内角时,直接写出此时t的值.


-
(1) 已知△ABC与△DEF(点D、E、F都是格点)成位似图形,则位似中心M的坐标是;
-
(2) △ABC外接圆半径是;
-
(3) 请在网格图中画一个格点△A1B1C1 , 使△A1B1C1∽△DEF,且相似比为1:2.
 =
=  .
. 
-
(1) 求证:△ADF∽△ACG;
-
(2) 若
 =
= 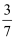 ,求
,求  的值.
的值.
 与
与  的相似比为1:3,则
的相似比为1:3,则  与
与  的面积比为( )
的面积比为( )
- 写出下列程序的运行结果.a=input(“a=”);if a>=0 m=a*a-1; print(%io(2)
- 阅读短文,判断下列句子是否符合短文内容。符合的写“A”,不符合的写“B”。Water is the most impor
- .有位史学家这样评论战国时期的“诸子百家”:“战国时代,诸子百家风行一时,各家中有顺势而活动的,想要因势利导,借助权力来
- 对某动物细胞进行荧光标记实验,如下示意图所示,其基本过程:①用某种荧光材料标记该动物细胞,细胞表面出现荧光斑点。②用激光
- 某温度下,w g某物质在足量氧气中充分燃烧,其燃烧产物立即与过量的Na2O2反应,固体质量增加w g。在①H2 ②C
- T℃时,体积均为0.5L的两个恒容密闭容器中发生可逆反应2A(g)+B(g) 2C(g) △H=-Q kJ/mol (Q
- 病人输液用的葡萄糖注射液是葡萄糖(化学式为C6H12O6)的水溶液,其标签上的部分内容如下图所示。利用标签所提供的信息,
- 已知向量a=(x+z,3),b=(2,y-z),且a⊥b,若x,y满足不等式|x|+|y|≤1,则z的取值范围为().
- 两千多年前,孔子提出了“君子和而不同”的思想。这一思想对中华文化产生了深远影响。“和而不同”反映了中华文化具有的特点是
- 今天的民众获得自由表达意见、畅所欲言、不受严密控制的观念的权力,主要得益于( ) A.罗马法系 B.
- 2017年11月1日,中国环境网报道,近日,从中科院大连化物所获悉,该所催化基础国家重点实验室王集杰博士、李灿院士等人
- 阅读下面的材料,根据要求写一篇不少于800字的文章。(60分)生活如镜,“时时勤拂拭,莫使惹尘埃。”花鸟、天气、万物皆因
- (4分)物体以5m/s的初速度沿光滑斜槽向上做直线运动,经4 s滑回原处时速度大小仍为 5 m/s,则物体的速度变化为
- 北半球夏至日到秋分日,下列现象正确的是( ) A.北极圈及其以北的极昼范围逐渐扩大B.南极圈及其以南地区的极夜范围
- V mL Al2(SO4)3溶液中含有Al3+m g,取 mL该溶液用水稀释至4V mL,则SO物质的量浓度为 () A
- (本题共16分) 已知:碱金属或碱土金属(Ⅱ族)与H2在隔绝空气加热时要以发生反应,生成离子型金属氢化物,如NaH、Ca
- 下列叙述错误的是:A.远视眼是由于晶状体太薄或眼球距离过短造成的;B.远处射来的光经过近视眼的水晶体折射,只能在视网膜后
- 在高200米的山顶上,测得山下一塔顶与塔底的俯角分别为30o、60o,则塔高为( ) A.米 B.
- 若对满足条件x+y+3=xy (x>0,y>0)的任意x、y,(x+y)2-a(x+y)+1≥0恒成立,则实数a的取值范
- 设 , 若有且仅有三个解,则实数的取值范围是( )A. B. C



