8 相似三角形的性质 知识点题库
如果两个相似三角形的对应中线的比为1:2,且它们的面积之和为30,则其中较小三角形的面积为( )
A . 6
B . 10
C . 24
D . 20
将一个三角形改成与它相似的三角形,如果面积扩大为原来的9倍,那么周长扩大为原来的( )
A . 9倍
B . 3倍
C . 81倍
D . 18倍
将直角三角形的三条边长同时扩大同一倍数,得到的三角形是( )
A . 钝角三角形
B . 锐角三角形
C . 直角三角形
D . 等腰三角形
如图,在△ABC中,D为AC边上一点,∠DBC=∠A.

-
(1) 求证:△BCD∽△ACB;
-
(2) 如果BC=
 ,AC=3,求CD的长.
,AC=3,求CD的长.
若两个相似三角形的面积比为1:4,则这两个相似三角形的周长比是.
如图,正方形ABCD的边长是16,点E在边AB上,AE=3,动点F在边BC上,且不与点B、C重合,将△EBF沿EF折叠,得到△EB′F.

-
(1) 当∠BEF=45°时,求证:CF=AE;
-
(2) 当B′D=B′C时,求BF的长;
-
(3) 求△CB′F周长的最小值.
如图,在矩形纸片ABCD中,已知AB=1,BC=  ,点E在边CD上移动,连接AE,将多边形ABCE沿直线AE翻折,得到多边形AB′C′E,点B、C的对应点分别为点B′、C′.
,点E在边CD上移动,连接AE,将多边形ABCE沿直线AE翻折,得到多边形AB′C′E,点B、C的对应点分别为点B′、C′.

-
(1) 当B′C′恰好经过点D时(如图1),求线段CE的长;
-
(2) 若B′C′分别交边AD,CD于点F,G,且∠DAE=22.5°(如图2),求△DFG的面积;
-
(3) 在点E从点C移动到点D的过程中,求点C′运动的路径长.
如图所示,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(﹣1,0)、(0,﹣3).

-
(1) 求抛物线的函数解析式;
-
(2) 点E为抛物线的顶点,点C为抛物线与x轴的另一交点,点D为y轴上一点,且DC=DE,求出点D的坐标;
-
(3) 在第二问的条件下,在直线DE上存在点P,使得以C、D、P为顶点的三角形与△DOC相似,请你直接写出所有满足条件的点P的坐标.
若两个三角形的相似比为3:4,则这两个三角形的面积比为.
已知△ABC∽△DEF,面积比为9:4,则△ABC与△DEF的对应边之比为( )
A . 3:4
B . 2:3
C . 9:16
D . 3:2
相似三角形的最短边分别是5cm和3cm,它们的面积之差为  ,那么小三角形的面积为( )
,那么小三角形的面积为( )
 ,那么小三角形的面积为( )
,那么小三角形的面积为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC上,QM在边BC上,若BC=8cm,AD=6cm,且PN=2PQ,则矩形PQMN的周长为( )

A . 14.4cm
B . 7.2cm
C . 11.52cm
D . 12.4cm
如图,已知△ABC和△PBD都是正方形网格上的格点三角形(顶点为网格线的交点),要使ΔABC∽ΔPBD,则点P的位置应落在( )


A . 点上
B . 点  上
C . 点
上
C . 点  上
D . 点
上
D . 点  上
上
 上
C . 点
上
C . 点  上
D . 点
上
D . 点  上
上
已知点G是  的重心,
的重心,  ,那么点G与边
,那么点G与边  中点之间的距离是.
中点之间的距离是.
 的重心,
的重心,  ,那么点G与边
,那么点G与边  中点之间的距离是.
中点之间的距离是.
如图,在 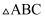 中,
中,  ,分别以
,分别以 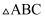 的边向外作正方形,连接EC、BF,过B作
的边向外作正方形,连接EC、BF,过B作  于M,交AC于N,下列结论:
于M,交AC于N,下列结论:
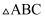 中,
中,  ,分别以
,分别以 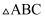 的边向外作正方形,连接EC、BF,过B作
的边向外作正方形,连接EC、BF,过B作  于M,交AC于N,下列结论:
于M,交AC于N,下列结论:  ≌
≌  ;
;  ;
;  ;
;  ,其中正确的是( )
,其中正确的是( )

A .  B .
B .  C .
C . 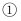 D .
D . 
 B .
B .  C .
C . 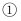 D .
D . 
如图,在矩形ABCD中,AB=3,BC=4.动点P从点A出发沿AC向终点C运动,同时动点Q从点B出发沿BA向点A运动,到达A点后立刻以原来的速度沿AB返回.点P,Q运动速度均为每秒1个单位长度,当点P到达点C时停止运动,点Q也同时停止.连结PQ,设运动时间为t(t >0)秒.


-
(1) 当点Q从B点向A点运动时(未到达A点),若△APQ ∽△ABC,求t的值;
-
(2) 伴随着P,Q两点的运动,线段PQ的垂直平分线为直线l.
①当直线l经过点A时,射线QP交AD边于点E,求AE的长;
②是否存在t的值,使得直线l经过点B?若存在,请求出所有t的值;若不存在,请说明理由.
如图,赵师傅透过平举的放大镜从正上方看水平桌面上的菱形图案的一角,那么∠A与放大镜中的∠C的大小关系是( )

A . ∠A=∠C
B . ∠A>∠C
C . ∠A<∠C
D . 无法比较
如图,已知△ABC中高AD恰好平分边BC,∠B=30°,点P是BA延长线上一点,点O是线段AD上一点且OP=OC,下面的结论:

①AC=AB;②∠APO+∠DCO=30°;
③△OPC是等边三角形; ④AC=AO+AP.
其中正确的为( )
A . ①②③
B . ①②④
C . ①③④
D . ①②③④
两个相似三角形的面积比为1:9,则它们的周长比为.
下列命题是真命题的是( )
A . 平行四边形的对角线相等
B . 相似三角形对应周长的比等于相似比的平方
C . 圆内接四边形的对角互补
D . 三角形的内心是三边的垂直平分线的交点
最近更新
- 空气是一种宝贵的自然资源.下列措施中,不利于提高空气质量的是() A.开发新能源代替化石燃料 B.改进汽车尾气的净化技术
- 地理信息技术现在已经应用于资源清查、城乡规划、灾害监测、环境管理、宏观决策等许多方面。下图是“某地城乡规划图”,此图是一
- 如图,在Rt△ABC中, ∠C=90,AB=5,AC=3,则的值是 A.B.C.D.
- C3N4是一种新型材料,它的硬度比金刚石还高,可做切割工具.在C3N4中,C的化合价为+4,则N的化合价是() A.+5
- 下列地区中,既是我国最主要的工业区,也是我国主要的农业基地是() A.江汉平原 B.珠江三角洲 C.洞庭
- 张华的胸围差是9厘米,李强的胸围差是12厘米,这说明 A. 张华比李强瘦弱 B.
- 现有两个边长不等的正方形,如图所示,且Aa、Bb、Cc、Dd间距相等。在AB、AC、CD、DB的中点分别放等量的正电荷或
- 在四边形ABCD中,若=a,=b,且|a+b|=|a-b|,则四边形的形状是_________________.
- 一简谐横波在x轴上传播,波源振动周期T=0.1 s,在某一时刻的波形如图11-1所示,且此时a点向下运动,则( )
- 要恢复和建设西北地区的生态环境,就必须:
- log3(lg x)=1.
- 下列选项中与林则徐“海纳百川,有容乃大”的名句所包含的文化生活道理一致的是() A.实现文化创新,需要博采众长 B.要以
- 设F1,F2分别是双曲线-=1(a>0,b>0)的左、右焦点,若双曲线右支上存在一点P,使=0(O为坐标原点
- “惜秦皇汉武,……唐宗宋祖……”。提及的汉武帝,他统治的核心思想是 A.儒家思想 B.道家思想
- 在下面语段的空白处,填上恰当的一句是( ) 六月,并不是好时候,没有春光,没有雪,没有秋意。那几天有的是
- 室温下向10 mL 0.1 mol/L的醋酸溶液中加水稀释并达到新平衡后,下列说法正确的是() A.溶液中导电粒子的数目
- 已知:如图,ABC中,AB=AC,BD和CE为ABC的高,BD和CE相交于点O。求证:OB=OC.
- 乙醇分子中各化学键如下图所示,下列选项对乙醇在各反应中断键情况的说明错误的是A、和金属钠作用时,键①断裂B、和浓H2SO
- Wu Dong runs faster than _________in this class.A. the other
- 16世纪末,伽利略通过比萨斜塔的自由落体试验推翻了亚里士多德关于物体的降落速度与物体的重量成正比的说法。这一事例说明 A



