8 相似三角形的性质 知识点题库
在同一时刻,身高1.6m的小强的影长是1.2m,旗杆的影长是15m,则旗杆高为( )
A . 16m
B . 18m
C . 20m
D . 22m
在下列命题中,真命题是( ).
A . 两个钝角三角形一定相似
B . 两个等腰三角形一定相似
C . 两个直角三角形一定相似
D . 两个等边三角形一定相似
下列命题中,正确的是( )
A . 如果一条直线截三角形两边的延长线所得的对应线段成比例,那么这条直线一定平行于三角形的第三边;
B . 不同向量的单位向量的长度都相等,方向也都相同;
C . 相似三角形的中线的比等于相似比;
D . 一般来说,一条线段的黄金分割点有两个.
△ABC的三边长分别为5,12,13,与它相似的△DEF的最小边长为15,则△DEF的周长为
若两个相似三角形的面积之比为1:2,则它们的周长之比为( )
A . 1:2
B . 1:4
C . 1:3
D . 1: 

已知矩形ABCD中,AD=6,AB=12,P为边CD上的动点,过A点作AQ⊥AP,交CB的延长线于点Q,交AB于点E,若DP=x,CQ=y,

-
(1) 试写出y与x的函数关系式.
-
(2) 当x为何值时,△APE为等腰直角三角形?
-
(3) 直接写出P点由D向C运动过程中,PQ的中点F运动的路径的长?
 的三边长分别为
的三边长分别为  ,
,  ,
,  ,与它相似的
,与它相似的  的最小边长为
的最小边长为  ,则
,则  的周长为.
的周长为.
如图,BC平分∠ABD,AB=4,BD=6,当BC=时,△ABC∽△CBD.

如图,矩形ABCD中,AB=4,BC=m(m>1),点E是AD边上一定点,且AE=1.

-
(1) 当m=3时,AB上存在点F,使△AEF与△BCF相似,求AF的长度.
-
(2) 如图②,当m=3.5时.用直尺和圆规在AB上作出所有使△AEF与△BCF相似的点F.(不写作法,保留作图痕迹)
-
(3) 对于每一个确定的m的值,AB上存在几个点F,使得△AEF与△BCF相似?
如图,△ABC内接于⊙O,BD⊥AC于点E,连接AD,OF⊥AD于点F,∠D=45°.若OF=1,则BE的长为.

如图,在 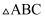 中,
中,  ,点E在边BC上移动(点E不与点B、C重合),满足
,点E在边BC上移动(点E不与点B、C重合),满足  ,且点D、F分别在边AB、AC上.
,且点D、F分别在边AB、AC上.
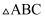 中,
中,  ,点E在边BC上移动(点E不与点B、C重合),满足
,点E在边BC上移动(点E不与点B、C重合),满足  ,且点D、F分别在边AB、AC上.
,且点D、F分别在边AB、AC上. 
-
(1) 求证:
 ;
;
-
(2) 当点E移动到BC的中点时,求证:FE平分
 .
.
如图,在平面直角坐标系内,Rt△ABC的点A在第一象限,点B与点A关于原点对称,∠C=90°.AC与  轴交于点D,点E在
轴交于点D,点E在  轴上,CD=2AD. 若AD平分∠OAE,△ADE的面积为1,则△ABC的面积为( )
轴上,CD=2AD. 若AD平分∠OAE,△ADE的面积为1,则△ABC的面积为( )
 轴交于点D,点E在
轴交于点D,点E在  轴上,CD=2AD. 若AD平分∠OAE,△ADE的面积为1,则△ABC的面积为( )
轴上,CD=2AD. 若AD平分∠OAE,△ADE的面积为1,则△ABC的面积为( ) 
A . 6
B . 9
C . 12
D . 15
通过一个3倍的放大镜看一个△ABC , 下面说法正确的是( )
A . △ABC放大后,∠A是原来的3倍
B . △ABC放大后周长是原来的3倍
C . △ABC放大后,面积是原来的3倍
D . 以上都不对
如果两个相似三角形的相似比为2:3,那么这两个三角形的面积比为( )
A . 2:3
B .  :
:  C . 4:9
D . 9:4
C . 4:9
D . 9:4
 :
:  C . 4:9
D . 9:4
C . 4:9
D . 9:4
已知  ∽
∽  ,相似比为3:1,若
,相似比为3:1,若  的面积为5,则
的面积为5,则  的面积为 .
的面积为 .
 ∽
∽  ,相似比为3:1,若
,相似比为3:1,若  的面积为5,则
的面积为5,则  的面积为 .
的面积为 .
如图,正方形ABCD的边长为2,  ,
,  线段MN的两端在CD,AD上滑动,当
线段MN的两端在CD,AD上滑动,当  与以D,M,N为顶点的三角形相似时,DM的长为( )
与以D,M,N为顶点的三角形相似时,DM的长为( )
 ,
,  线段MN的两端在CD,AD上滑动,当
线段MN的两端在CD,AD上滑动,当  与以D,M,N为顶点的三角形相似时,DM的长为( )
与以D,M,N为顶点的三角形相似时,DM的长为( ) 
A .  B .
B .  或
或  C .
C .  D .
D .  或
或 
 B .
B .  或
或  C .
C .  D .
D .  或
或 
如图,在  中,点
中,点  分别是
分别是  的中点,连接
的中点,连接  ,四边形
,四边形  的面积记作
的面积记作 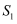 ;点
;点  分别是
分别是  的中点,连接
的中点,连接  ,四边形
,四边形  的面积记作
的面积记作  …,按此规律进行下去,若
…,按此规律进行下去,若  ,则
,则  ;
;  .(
.(  为正整数)
为正整数)
 中,点
中,点  分别是
分别是  的中点,连接
的中点,连接  ,四边形
,四边形  的面积记作
的面积记作 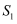 ;点
;点  分别是
分别是  的中点,连接
的中点,连接  ,四边形
,四边形  的面积记作
的面积记作  …,按此规律进行下去,若
…,按此规律进行下去,若  ,则
,则  ;
;  .(
.(  为正整数)
为正整数) 
如图,  ,
,  ∠BAD
∠BAD
 ,
,  ∠BAD
∠BAD 
-
(1) 在AC上方求作求作一点E,使得△ACE∽△ABD(要求:尺规作图,保留作图痕迹,不写作法)
-
(2) 在(1)的条件下,连接DE,若
 ,
,  ,求证:
,求证: 
如图所示的正方形网格中,每个小正方形的边长均为1,A、B、C、E、F均在格点上.若△ABC∽△DFE,则△DFE的面积是.

下列说法正确的是( )
A . 对角线相等的四边形是矩形.
B . 相似三角形的面积的比等于相似比.
C . 方差越大,数据的波动越大;方差越小,数据的波动越小.
D . 过一点有且只有一条直线与已知直线平行.
最近更新
- 过去30多年中国的发展使许多与中国合作的国家广为受益。向世界传递“正能量”需要我国( )①坚定维护自身利益,保持自身利
- 下列属于植物芳香油理化性质的是() ①具有较强的挥发性 ②易溶于水 ③易溶于有机溶剂 ④具有特殊植物香味 A.①②③
- 动物在生态系统中有重要作用,因为动物( )A.是食物的唯一来源 B能固定二氧化碳C
- 阅读右边的程序框图,运行相应的程序,若输入的值为-4,则输出的值为 A.,0.5
- 右图表示雄果蝇细胞分裂过程中DNA含量的变化。下列叙述中,正确的是 A.若图1表示减数分裂,则图1的CD段表示同源染色体
- 已知:如图,∠A0B的两边 0A、0B均为平面反光镜,∠A0B=.若平行于OB的光线经点Q反射到P,则∠QPB=(
- 问题探究:某社区道路年久失修,下雨天污水横流;卫生脏乱差;社区居民打麻将赌博成风;社区治安差,经常有失窃、打架斗殴现象发
- 已知函数,则关于的方程给出下列四个命题: ①存在实数,使得方程恰有1个实根;②存在实数,使得方程恰有2个不相等的实根;
- 一个交流电压的瞬时值表达式为u=15sin100πt V,将该交流电加在一电阻上时,产生的电功率为25 W,那么这个电阻
- 据了解,在发达国家,工资一般会占企业运营成本50%左右,而在中国则不到10%。发达国家劳动报酬在国民收入中所占的比重一般
- 已知是圆内过点的最短弦,则=( )
- 现有5.6g的生铁与足量的稀硫酸完全反应,产生氢气的质量是A.等于0.2g B.小于0.2g
- As you know, it is my duty to ________ my younger sisters fr
- 跨国公司在全球范围内寻找最优区位,应( ) A.选择在经济实力强的地区和国家 B.选择在经济实力薄弱的地区和国家
- 下列离子方程式书写正确的是A. 铝片放入NaOH溶液中:2Al+2OH-=2AlO2-+H2↑B. 碳酸钙溶于醋酸中:C
- 你认为下面哪种行为不是自信的表现 ( )A.遇到问题向老
- 12细胞的结构和功能是相适应的,下列叙述中正确的是() A.蛋白质合成旺盛的细胞中,其核仁较大,染色体数目较多B.细胞膜
- 函数与在同一平面直角坐标系下的图像大致是
- 鲁尔区传统的工业部门大多属于( ) A.资金密集型工业
- 寒冷的味道 (黄明山)寒冷离我们越来越远了。有人说,地球变得越来越热了。还说有一种厄尔尼诺现象。对此,我说不出个子丑寅



