8 相似三角形的性质 知识点题库
已知△ABC∽△DEF,∠A=∠D,∠C=∠F且AB:DE=1:2,则EF:BC=.
【探究证明】
-
(1)
某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.
如图1,矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H.求证:
 =
=  ;
;【结论应用】

-
(2)
如图2,在满足(1)的条件下,又AM⊥BN,点M,N分别在边BC,CD上,若
 =
= 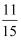 ,则
,则  的值为;
的值为;【联系拓展】

-
(3)
如图3,四边形ABCD中,∠ABC=90°,AB=AD=10,BC=CD=5,AM⊥DN,点M,N分别在边BC,AB上,求
 的值.
的值.
如图①,在△ABC中,AB=AC,BC=acm,∠B=30°.动点P以1cm/s的速度从点B出发,沿折线B﹣A﹣C运动到点C时停止运动.设点P出发x s时,△PBC的面积为y cm2 . 已知y与x的函数图象如图②所示.请根据图中信息,解答下列问题:

-
(1) 试判断△DOE的形状,并说明理由;
-
(2) 当a为何值时,△DOE与△ABC相似?
如图,甲、乙两人分别从A(1,  )、B(6,0)两点同时出发,点O为坐标原点,甲沿AO方向、乙沿BO方向均以4km/h的速度行驶,th后,甲到达M点,乙到达N点.
)、B(6,0)两点同时出发,点O为坐标原点,甲沿AO方向、乙沿BO方向均以4km/h的速度行驶,th后,甲到达M点,乙到达N点.
 )、B(6,0)两点同时出发,点O为坐标原点,甲沿AO方向、乙沿BO方向均以4km/h的速度行驶,th后,甲到达M点,乙到达N点.
)、B(6,0)两点同时出发,点O为坐标原点,甲沿AO方向、乙沿BO方向均以4km/h的速度行驶,th后,甲到达M点,乙到达N点. 
-
(1) 请说明甲、乙两人到达O点前,MN与AB不可能平行;
-
(2) 当t为何值时,△OMN∽△OBA;
-
(3) 甲、乙两人之间的距离为MN的长,设s=MN2 , 求s与t之间的函数关系式,并求甲、乙两人之间距离的最小值.
若△ABC~△A′B′C′,面积比为1:4,则△ABC与△A′B′C′的相似比为( )
A . 16:1
B . 1:16
C . 2:1
D . 1:2
如图,将△ABC绕点B按逆时针方向旋转得到△EBD,点E、点D分别与点A、点C对应,且点D在边AC上,边DE交边AB于点F,△BDC∽△ABC.已知BC= 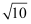 ,AC=5,那么△DBF的面积等于.
,AC=5,那么△DBF的面积等于.
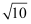 ,AC=5,那么△DBF的面积等于.
,AC=5,那么△DBF的面积等于. 
如图,抛物线y=  x2+bx+c与x轴交于A、B两点,与y轴交于点C,其对称轴交抛物线于点D,交x轴于点E,已知OB=OC=6.
x2+bx+c与x轴交于A、B两点,与y轴交于点C,其对称轴交抛物线于点D,交x轴于点E,已知OB=OC=6.

-
(1) 求抛物线的解析式及点D的坐标;
-
(2) 连接BD,F为抛物线上一动点,当∠FAB=∠EDB时,求点F的坐标;
-
(3) 平行于x轴的直线交抛物线于M、N两点,以线段MN为对角线作菱形MPNQ,当点P在x轴上,且PQ=
 MN时,求菱形对角线MN的长.
MN时,求菱形对角线MN的长.
在Rt△ABC中,∠ACB=90°,点D在边AC上,DE⊥B于点E,连CE.
-
(1)
如图1,已知AC=BC,AD=2CD,

①△ADE与△ABC面积之比;
②求tan∠ECB的值;
-
(2)
如图2,已知
 =
=  =k,求tan∠ECB的值(用含k的代数式表示).
=k,求tan∠ECB的值(用含k的代数式表示).
如图,在  中,
中, 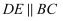 ,
, 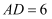 ,
,  ,则
,则  的值为( ).
的值为( ).
 中,
中, 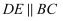 ,
, 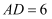 ,
,  ,则
,则  的值为( ).
的值为( ).
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,DE∥BC,CD与BE相交于点O,若  ,则
,则  的值为( )
的值为( )
 ,则
,则  的值为( )
的值为( ) 
A .  B .
B .  C .
C . 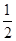 D .
D . 
如图,  中,
中,  ,
,  ,
,  ,
,  是
是  边的中点,
边的中点,  是
是  边上一动点(点
边上一动点(点  不与
不与  、
、  重合),若以
重合),若以  、
、  、
、  为顶点的三角形与
为顶点的三角形与  相似,则线段
相似,则线段  .
.
 中,
中,  ,
,  ,
,  ,
,  是
是  边的中点,
边的中点,  是
是  边上一动点(点
边上一动点(点  不与
不与  、
、  重合),若以
重合),若以  、
、  、
、  为顶点的三角形与
为顶点的三角形与  相似,则线段
相似,则线段  .
. 
把Rt△ABC和Rt△DEF按如图①摆放(点C与E重合),点B、C(E)、F在同一条直线上.已知:∠ACB=∠EDF=90°,∠DEF=45°,AC=8,BC=6,EF=10.如图②,△DEF从图①的位置出发,以每秒1个单位的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点A出发,以每秒1个单位的速度沿AB向点B匀速移动;当点P移动到点B时,点P停止移动,△DEF也随之停止移动.DE与AC交于点Q,连接PQ,设移动时间为t(s).

-
(1) △DEF在平移的过程中,AP=CE=(用含t的代数式表示);当点D落在Rt△ABC的边AC上时,求t的值.
-
(2) 在移动过程中,当0<t≤5时,连接PE,
①设四边形APEQ的面积为y,求y与t之间的函数关系式并试探究y的最大值;
②是否存在△PQE为直角三角形?若存在,请直接写出t的值;若不存在,请说明理由.
如图,在一斜边长30cm的直角三角形木板(即Rt△ACB)中截取一个正方形CDEF, 点D在边BC上,点E在斜边AB上,点F在边AC上,若AF:AC=1:3,则这块木板截取正方形CDEF后,剩余部分的面积为( )

A . 200cm2
B . 170cm2
C . 150cm2
D . 100 cm2
如图,在△ABC中,DE∥BC,EF∥AB.

-
(1) 求证:△ADE∽△EFC;
-
(2) 如果AB=6,AD=4,求
 的值.
的值.
如图,是由6  6个边长为1的小正方形网格组成,每个小正方形的顶点称为格点,△ABC的三个顶点A,B,C均在格点上,请仅用无刻度的直尺,按下列要求画图.
6个边长为1的小正方形网格组成,每个小正方形的顶点称为格点,△ABC的三个顶点A,B,C均在格点上,请仅用无刻度的直尺,按下列要求画图.
 6个边长为1的小正方形网格组成,每个小正方形的顶点称为格点,△ABC的三个顶点A,B,C均在格点上,请仅用无刻度的直尺,按下列要求画图.
6个边长为1的小正方形网格组成,每个小正方形的顶点称为格点,△ABC的三个顶点A,B,C均在格点上,请仅用无刻度的直尺,按下列要求画图. 
-
(1) 在图1中找一个格点D ,使以点A、B、C、D为顶点的四边形是平行四边形(画出一种情况即可)
-
(2) 在图2中仅用无刻度的直尺,把线段AB三等分(保留画图痕迹,不写画法)
如图,在平面直角坐标系  中,直线
中,直线  与
与  轴交于点
轴交于点  ,与
,与  轴交于点
轴交于点  抛物线
抛物线 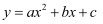 的对称轴是直线
的对称轴是直线  与
与  轴的交点为点
轴的交点为点  且经过点
且经过点  两点.
两点.
 中,直线
中,直线  与
与  轴交于点
轴交于点  ,与
,与  轴交于点
轴交于点  抛物线
抛物线 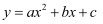 的对称轴是直线
的对称轴是直线  与
与  轴的交点为点
轴的交点为点  且经过点
且经过点  两点.
两点. 
-
(1) 求抛物线的解析式;
-
(2) 点
 为抛物线对称轴上一动点,当
为抛物线对称轴上一动点,当  的值最小时,请你求出点
的值最小时,请你求出点  的坐标;
的坐标;
-
(3) 抛物线上是否存在点
 ,过点
,过点  作
作  轴于点
轴于点  使得以点
使得以点  为顶点的三角形与
为顶点的三角形与  相似?若存在,请直接写出点
相似?若存在,请直接写出点  的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
如图,点D,E分别在△ABC的边AC,AB上,△ADE∽△ABC,M,N分别是DE,BC的中点,若  =
=  ,则
,则  =.
=.
 =
=  ,则
,则  =.
=.

如图,△ABC∽△ACD , 相似比为2,则S△BDC:S△DAC为( )

A . 4:1
B . 3:1
C . 2:1
D . 1:1
如果两个相似三角形的对应边之比为2:5,其中一个三角形的一个内角的角平分线长为7,则另一个三角形对应角平分线的长为( )
A .  B .
B . 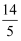 C .
C .  或
或 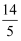 D . 无法确定
D . 无法确定
 B .
B . 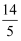 C .
C .  或
或 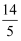 D . 无法确定
D . 无法确定
如图所示,抛物线与x轴交于A、B两点,与y轴交于点C,且 ,
,  ,
,  , 抛物线的对称轴与直线BC交于点M,与x轴交于点N.
, 抛物线的对称轴与直线BC交于点M,与x轴交于点N.
 ,
,  ,
,  , 抛物线的对称轴与直线BC交于点M,与x轴交于点N.
, 抛物线的对称轴与直线BC交于点M,与x轴交于点N.
-
(1) 求抛物线的解析式;
-
(2) 若点P是对称轴上的一个动点,是否存在以P、C、M为顶点的三角形与
 相似?若存在,求出点P的坐标,若不存在,请说明理由.
相似?若存在,求出点P的坐标,若不存在,请说明理由.
-
(3) D为CO的中点,一个动点G从D点出发,先到达x轴上的点E,再走到抛物线对称轴上的点F,最后返回到点C.要使动点G走过的路程最短,请找出点E、F的位置,写出坐标,并求出最短路程.
最近更新
- 阅读下面这首诗,然后回答问题(共3分)春望杜甫国破山河在,城春草木深。感时花溅泪,恨别鸟惊心。烽火连三月,家书抵万金。白
- 已知铍(Be)的原子序数为4,下列对铍及其化合物的叙述中,正确的是 ( )A、铍的原子半径大于硼的原
- 侧棱长为1的正三棱锥四个顶点在一个球面上,球心在正三棱锥的底面上,则该球的表面积为( )A.π
- 向沸水中滴加几滴饱和氯化铁溶液并继续煮沸至溶液呈红褐色时停止加热,此时当光束通过该红褐色液体时,从侧面可观察到一条光亮的
- 将基因定位于染色体上的科学家是 A.沃森和克里克 B.摩尔根 C.孟德尔 D.卡尔
- 西欧奴隶制度终结的标志是() A、公元395年,帝国分裂 B、公元1世纪,基督教
- 下列生命活动过程中高尔基体参与的是 A.植物细胞壁的形成 B.分解葡萄糖产生ATP C.
- 18世纪的英国因拥有广大的殖民地而号称“日不落帝国”,其中,被誉为“英王王冠上的一颗最明亮的宝石”指的是下列哪个国家?(
- 下列关于简谐振动和简谐机械波的说法正确的是( ) A.弹簧振子的周期与振幅有关 B.横波在介质中的传播速度由介质本身的
- He is easy to be homesick so I’ afraid whether he can ______
- 下列填入文中括号内的语句,衔接最恰当的一项是( )研究人员希望最新发现能为治疗沙门氏菌感染提供新思路。目前,治疗沙门氏菌
- 一种口服液有大、小盒两种包装,3大盒、4小盒共装108瓶,2大盒、3小盒共装76瓶.大盒与小盒每盒各装多少瓶?
- .Three university departments have been _______ $ 600,000 to
- The tramp in the film was loved for his optimism and determi
- 某同学在“研究动滑轮特点”的实验时进行了正确的操作,并记录了数据,分析数据后发现,结果与课本上“使用动滑轮省力一半”不符
- 已知等腰三角形的两条边长分别是2和4,则它的周长是( ) A.8 B. 8或10 C.
- 农民消费不足一直是制约我国内需扩大的瓶颈之一。国家自2008年12月1日起推行新的“家电下乡”试点,农户购买“家电下乡”
- 人类大量开采使用煤炭、石油、天然气等矿物燃料,将使地壳中减少的元素是( ) A.碳元素
- 综合性学习。(7分) 亲爱的同学,你们班要举行“微笑着面对生活”综合性学习活动,请你来参与。 (1)请你为本次活动设计一
- 下列叙述中正确的是( )A.除零族元素外,短周期元素的最高化合价在数值上都等于该元素所属的族序数B.除短周期外,其他



