8 相似三角形的性质 知识点题库
已知△ABC∽△DEF,若△ABC与△DEF的面积比为9:1,则△ABC与△DEF对应角的角平分线之比为.
若△ABC~△DEF,相似比为3:2,则对应高的比为( )
A . 3:2
B . 3:5
C . 9:4
D . 4:9
如图,已知△ABC∽△DEF,AB:DE=1:2,则下列等式一定成立的是( )

A .  =
=  B .
B .  =
=  C .
C .  =
=  D .
D .  =
= 
 =
=  B .
B .  =
=  C .
C .  =
=  D .
D .  =
= 
若△ABC∽△DEF,相似比为2:3,则S△ABC:S△DEF=.
如图1,在平面直角坐标系中,抛物线y=ax2+bx+3交x轴于A(﹣1,0)和B(5,0)两点,交y轴于点C,点D是线段OB上一动点,连接CD,将线段CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴于H,交抛物线于点M,过点C作CF⊥l于F.

-
(1) 求抛物线解析式;
-
(2)
如图2,当点F恰好在抛物线上时(与点M重合)

①求点F的坐标;
②求线段OD的长;
③试探究在直线l上,是否存在点G,使∠EDG=45°?若存在,请直接写出点G的坐标;若不存在,请说明理由.
-
(3) 在点D的运动过程中,连接CM,若△COD∽△CFM,请直接写出线段OD的长.
如图,直线y=  x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
 x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
-
(1) 求抛物线F1所表示的二次函数的表达式及顶点Q的坐标;
-
(2) 在抛物线上是否存在点P,使△BPC的内心在y轴上,若存在,求出点P的坐标,若不存在写出理由;
-
(3) 直线y=kx﹣6与y轴交于点N,与直线AC的交点为M,当△MNC与△AOC相似时,求点M坐标.
如图,已知P为△ABC内一点,过P点分别作直线平行于△ABC的各边,形成小三角形的面积S1、S2、S3 , 分别为4、9、49,则△ABC的面积为.

已知△ABC~△DEF, BC边上的高与EF边上的高之比为2:3,则△ABC与△DEF的面积的比为.
如图,△ABC中,∠ACB>∠ABC .

-
(1) 用直尺和圆规在∠ACB的内部作射线CM , 使∠ACM=∠ABC(不要求写作法,保留作图痕迹);
-
(2) 若(1)中的射线CM交AB于点D , AB=9,AC=6,求AD的长.
 与
与 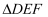 的相似比为
的相似比为  ,则
,则  与
与 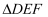 的周长比为( )
的周长比为( )
A . 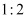 B .
B .  C .
C .  D .
D . 
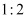 B .
B .  C .
C .  D .
D . 
图是5×5的网格图,每个小正方形的边长为1,请按要求作格点图形(图形的每个顶点都在格点上)

-
(1) 在图①中以线段PQ为一边作一个等腰直角三角形;
-
(2) 在图②中,作△DEF相似于△ABC,且△ABC与△DEF的相似比是1:
 .
.
如图,  中,
中, 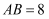 ,
,  ,
,  ,点
,点  在
在  内,且
内,且  平分
平分 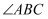 ,
, 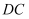 平分
平分  ,过点D作直线
,过点D作直线  ,分别交
,分别交  、
、  于点P、Q,若
于点P、Q,若  与
与  相似,则线段
相似,则线段  的长为( )
的长为( )
 中,
中, 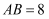 ,
,  ,
,  ,点
,点  在
在  内,且
内,且  平分
平分  ,
,  平分
平分  ,过点D作直线
,过点D作直线  ,分别交
,分别交  、
、  于点P、Q,若
于点P、Q,若  与
与  相似,则线段
相似,则线段  的长为( )
的长为( ) 
A . 5
B .  C . 5或
C . 5或  D . 6
D . 6
 C . 5或
C . 5或  D . 6
D . 6
如图,在正方形ABCD中,E,F分别是边AD,CD上的点,AE=ED,DF=  FC,连结EF交BC的延长线于点G.
FC,连结EF交BC的延长线于点G.
 FC,连结EF交BC的延长线于点G.
FC,连结EF交BC的延长线于点G. 
-
(1) 试说明:△ABE∽△DEF;
-
(2) 若正方形的边长为4,求BG的长.
若△ABC∼△DEF,相似比为3:2,则△ABC与△DEF的面积比为( )
A . 3:2
B . 9:4
C . 2:3
D . 4:9
如图,  平分
平分  且
且  ,则当
,则当  时,
时,  .
.
 平分
平分  且
且  ,则当
,则当  时,
时,  .
. 
在边长为1的正方形  中,
中,  是
是  的中点,
的中点,  ,
,  为垂足.求
为垂足.求 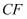 的长.
的长.
 中,
中,  是
是  的中点,
的中点,  ,
,  为垂足.求
为垂足.求 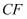 的长.
的长. 
已知一次函数  的图象与反比例函数
的图象与反比例函数  的图象在第一象限交于点
的图象在第一象限交于点  ,与
,与  轴交于点
轴交于点  ,与
,与  轴交于点
轴交于点  ,若
,若  ,且
,且  .
.
 的图象与反比例函数
的图象与反比例函数  的图象在第一象限交于点
的图象在第一象限交于点  ,与
,与  轴交于点
轴交于点  ,与
,与  轴交于点
轴交于点  ,若
,若  ,且
,且  .
. 
-
(1) 求反比例函数与一次函数的解析式;
-
(2) 直接写出
 的解集;
的解集;
-
(3) 若点
 为
为  轴上一点,求使
轴上一点,求使  的点
的点  的坐标.
的坐标.
如图,△ABC中,∠C=90°,AC=4cm,BC=3cm,动点P从点B出发以1cm/s速度向点C移动,同时动点Q从C出发以2cm/s的速度向点A移动,其中一个点到终点另一个点也随之停止.设它们的运动时间为t.

-
(1) 根据题意知:CQ=,CP=;(用含t的代数式表示);
-
(2) 运动几秒时,△CPQ与△CBA相似?
若  ,
,  ,
,  的面积为
的面积为  ,则
,则  的面积为
的面积为 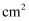 .
.
 ,
,  ,
,  的面积为
的面积为  ,则
,则  的面积为
的面积为 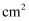 .
.
如图,已知 , 若
, 若 ,
,  ,
,  , 则AE的长是.
, 则AE的长是.
 , 若
, 若 ,
,  ,
,  , 则AE的长是.
, 则AE的长是.
最近更新
- 在等体积的pH值相等盐酸与醋酸溶液中,各加水稀释100倍,结果盐酸与醋酸的pH值_________(填“相等”或“不等”
- ------I have just had my watch repaired. ------How much did
- 在一个新鲜萝卜中挖一凹槽,在凹槽中放入浓盐水.一段时间后,萝卜变软,凹槽中水分增多.下列图示的实验与此实验原理差异最大的
- 下列这组图片与1992年后城市国有企业改革的哪项内容相关?( )A.改革管理体制,把所有权与经营权分开 B.改革所有
- 对于任意的直线l与平面a,在平面a内必有直线m,使m与l
- 阅读下文,完成14—17题。(16分) 苦 瓜 肖复兴 原来我家有个小院,院里可以种些花草和蔬菜。
- 12.补写出下列句子中的空缺部分。 (1)《诗经·氓》中用比兴手法写弃妇面容憔悴与被弃的痛苦的句子是:
- 一个长螺线管中通有电流,把一个带电粒子沿中轴线射入(若不计重力影响),粒子将在管中 A、做圆周运动B、沿轴线来回运
- 根据句意,从方框中选择恰当的单词或短语填空。allow, too many, wrong,guess, work ou
- 如图,有一半径为R的半圆形曲面MPQ,质量为2m的A球与质量为m的B球, 用轻质绳连接后挂在圆柱曲面边缘.现将A球从边缘
- It is high time for us to take measures to protect these old
- 下列各句中,没有语病的一句是 () A.为了总结开展“研究性学
- 圣琵琶传闻 有书生欲游吴地,道经江西,因风阻泊船,闲步入林,过①一僧院。僧已他出,房门外,小廊数间,傍有笔砚。书生攻②画
- I wonder _________Eddie has gone to Singapore.A.how longB.ho
- 我国对可呼吸的钠-二氧化碳电池的研究取得突破性进展,该电池的总反应式为: 4Na+3CO22Na2CO3+C,其工作原理
- 下列关于蛋白质和氨基酸的叙述,正确的是() A.具有生物催化作用的酶都是由氨基酸组成的 B.高等动物能合成生命活动所需的
- 14.阅读下面这首词,完成题目。 南柯子·忆旧 仲 殊 十里青山远,潮平路带沙。数声啼鸟怨年华,又是凄凉时候在天涯。
- 依次填入下面一段文字横线处的语句,与上下文衔接最恰当的一组是 发射窗口定在凌晨。___________。火箭______
- (2009.海南月考)下列有关村民自治的观点中,正确的是
- 新发明改变了我们的生活,同时出现了很多新的职业,下列职业按出现先后排序正确的是 A、电话接线员—火车司机—空姐—



