8 相似三角形的性质 知识点题库
如图1所示,若△ABC∽△DEF,则∠E的度数为( )
A . 28°
B . 32°
C . 42°
D . 52°
若两个相似多边形的面积之比为1:4,则它们的周长之比为( )
A . 1:4
B . 2:1
C . 1:2
D . 4:1
如图,在正方形ABCD中,E是BC上的一点,连结AE,作BF⊥AE,垂足为H,交CD于F,作CG∥AE,交BF于G.
求证:(1)CG=BH,
(2)FC2=BF·GF,
(3) =
= .
.
若两个相似三角形的周长比为1:3,则面积比为( )
A . 1:3
B . 3:1
C . 1:9
D . 9:1
如图,在直角坐标系中,  ,边
,边  、
、 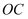 都在
都在  轴的正半轴上,点
轴的正半轴上,点  的坐标为
的坐标为  ,
,  ,
,  .反比例函数
.反比例函数  的图象经过点
的图象经过点  ,交
,交  边于点
边于点  .则
.则  的值为.
的值为.
 ,边
,边  、
、 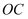 都在
都在  轴的正半轴上,点
轴的正半轴上,点  的坐标为
的坐标为  ,
,  ,
,  .反比例函数
.反比例函数  的图象经过点
的图象经过点  ,交
,交  边于点
边于点  .则
.则  的值为.
的值为. 
已知矩形ABCD中,E是BC的中点,DF⊥AE于点F.

-
(1) 如图1,若
 ,求AE·AF的值;
,求AE·AF的值;
-
(2) 如图2,连接AC交DF于点G,若
 ,求cos∠FCE的值;
,求cos∠FCE的值;
-
(3) 如图3,延长DF交AB于点G,若G点恰好为AB的中点,连接FC,过A作AK∥FC交FD于K,设△ADK的面积为S1 , △CDF的面积为S2 , 则
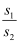 的值为.
的值为.
如图,已知矩形ABCD的边长AB=3cm,BC=6cm,某一时刻,动点M从点A出发沿AB方向以1cm/s的速度向点B匀速运动;同时,动点N从点D沿DA方向以2cm/s的速度向点A匀速运动.

-
(1) 经过多少时间,△AMN的面积等于矩形ABCD面积的
 ?
?
-
(2) 是否存在时刻t,使A、M、N为顶点的三角形与△ACD相似?若存在,求t的值;若不存在,请说明理由.
如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在图的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,求小桥所在圆的半径.

如图,在⊿ABC中,AB=BC,以BC为直径的⊙O交AC于点D,过D作DE⊥AB,DF⊥BC,垂足分别为E、F,

-
(1) 求证:
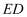 是⊙O的切线;
是⊙O的切线;
-
(2) 求证:
 ;
;
-
(3) 若
 ,
,  ,求⊙O的直径.
,求⊙O的直径.
如图,在平面直角坐标系中,已知A(1,0),D(3,0),△ABC与△DEF位似,原点O是位似中心,若△ABC的面积为5,则△DEF的面积为.

如图,n个全等的等腰三角形的底边在同一条直线上,底角顶点依次重合.连接第一个三角形的底角顶点 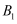 和第
和第  个三角形的顶角顶点
个三角形的顶角顶点  交
交  于点
于点  ,则
,则  .
.
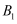 和第
和第  个三角形的顶角顶点
个三角形的顶角顶点  交
交  于点
于点  ,则
,则  .
.

当两个相似三角形的相似比为时,这两个相似三角形-定是-对全等三角形。
如图,  中,
中,  ,
,  ,
,  ,D是
,D是  边的中点,P是
边的中点,P是  边上一动点(点P不与B、C重合),若以D、C、P为顶点的三角形与
边上一动点(点P不与B、C重合),若以D、C、P为顶点的三角形与  相似,则线段
相似,则线段  .
.
 中,
中,  ,
,  ,
,  ,D是
,D是  边的中点,P是
边的中点,P是  边上一动点(点P不与B、C重合),若以D、C、P为顶点的三角形与
边上一动点(点P不与B、C重合),若以D、C、P为顶点的三角形与  相似,则线段
相似,则线段  .
. 
若△ABC∽△A’B’C’,且△ABC与△A’B’C’的面积之比为1:4,则相似比为.
两个相似三角形的相似比为1:2,则它们面积的比为( )
A . 1:4
B . 1:2
C . 1:  D . 4:1
D . 4:1
 D . 4:1
D . 4:1
如图,在正方形网格上有两个相似三角形△ABC和△DEF,则∠BAC的度数为.

如图,已知△ABC和△EDC是以点C为位似中心的位似图形,且△ABC和△EDC的位似比为1:2,△ABC面积为2,则△EDC的面积是( )

A . 2
B . 8
C . 16
D . 32
如图,  与
与  是位似图形,点
是位似图形,点  为位似中心,若
为位似中心,若  ,则
,则  与
与  的面积比为.
的面积比为.
 与
与  是位似图形,点
是位似图形,点  为位似中心,若
为位似中心,若  ,则
,则  与
与  的面积比为.
的面积比为. 
如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF=  DC,连接EF并延长交BC的延长线于点G.
DC,连接EF并延长交BC的延长线于点G.
 DC,连接EF并延长交BC的延长线于点G.
DC,连接EF并延长交BC的延长线于点G. 
-
(1) 求证:△ABE∽△DEF;
-
(2) 若正方形的边长为4,求BG的长.
如图,在△ABC中,AC=4.

-
(1) 在AC上求作一点D,连接BD,使得△ABD∽△ACB;(要求:尺规作图,不写作法,保留作图痕迹)
-
(2) 点M,N分别是BD、BC中点,若AD=1,求
 的值.
的值.
最近更新
- 下列语句中,加点的词语使用最恰当的一项是() A. 传说,屈原死后被一条大鱼驮回秭归,终于从流放之地回归楚国,这一切听起
- 如图,用平行于斜面的推力使物体静止于倾角为θ的固定斜面上,下列表述正确的是 A.斜面对物体的摩擦力一定沿斜面向下 B.斜
- 化合物AX3和单质X2在一定条件下反应可生成化合物AX5。回答下列问题: (1)已知AX3的熔点和沸点分别为-93.6
- 央行决定,自2015年10月24日起,下调金融机构人民币贷款和存款基准利率0.25个百分点;自同日起,下调金融机构人民币
- 根据化合价由高到低的顺序,在HClO4、 KClO3、 HClO2、( )、Cl2的排列中,括号内应填入下列物质中的
- 下列叙述正确的是() A. 硫酸钡难溶于水,在水溶液中不能导电,所以硫酸钡不是电解质 B. 电解质的电离一定要在水分子作
- Every time the train goes ____ the village, all the houses
- 下列物质中,不在核糖体上合成的是 A.麦芽糖酶 B.核糖核酸 C.肌球蛋白
- 关于文艺复兴运动,初三(3)班的同学展开了激烈讨论,你认为谁的看法是正确的? A.小李认为是一次复古运动 B.小王认为是
- 下面的文句,是陈毅的纪念鲁迅逝世十四周年写的一幅对联,请将其顺序重新整理,把序号填在横线上。 ①岂仅文坛闯将②要打叭儿落
- 如图所示,、两种单色光,平行地射到平板玻璃上,经平板玻璃后射出的光线分别为、。下列说法正确的是 A.光线的折射
- 22.在下面一段文字横线处补写恰当的语句,使整段文字语意完整连贯,内容贴切,逻辑严密。每处不超过l5个字。(5分) 字的
- 中国国家地震灾害紧急救援队曾多次走出国门执行救援任务,他们的出色表现展示和提高了中国的国家形象。利用救援外交这种公共外交
- 设函数对的一切实数均有。则等于_________
- 放射性在技术上有很多应用,不同的放射源可用于不同的目的。下表列出一些放射性同位素的半衰期和可利用的射线。若它们间空气中烟
- 19.重金属离子有毒性。实验室有甲、乙两种废液,均有一定毒性,甲废液经化验呈碱性,主要有毒离子为Ba2+离子,如将甲、乙
- 2011年10月15日至18日党的十七届六中全会在北京举行,会议审议通过了《中共中央关于深化文化体制改革、推动社会主义
- 将额定电压相同的两个灯泡L1、L2串联后接入电路中,如图所示。接通电路后发现L1要亮一些,则下列判断正确的是( )
- 作文。50分请以“游”为题写一篇文章。要求:①将题目补充完整;②必须写游记;③要有自己的体验和感悟,不得抄袭;④不少于5
- 关于细胞学说的建立过程,科学家与其观点不相符的是( ) A.虎克观察木栓组织,并命名为细胞B.列文虎克观察红细胞、



