8 相似三角形的性质 知识点题库
如图,∠ABD=∠BCD=90 ,AD=10,BD=6.如果两个三角形相似,则CD的长为 ( )
,AD=10,BD=6.如果两个三角形相似,则CD的长为 ( )
A . 3.6
B . 4.8
C . 4.8或3.6
D . 无法确定
平面直角坐标中,已知点O(0,0),A(0,2),B(1,0),点P是反比例函数y=﹣ 图象上的一个动点,过点P作PQ⊥x轴,垂足为Q.若以点O、P、Q为顶点的三角形与△OAB相似,则相应的点P共有( )
图象上的一个动点,过点P作PQ⊥x轴,垂足为Q.若以点O、P、Q为顶点的三角形与△OAB相似,则相应的点P共有( )

A . 1个
B . 2个
C . 3个
D . 4个
已知△ABC∽△DEF , 且它们的面积之比为4:9,则它们的相似比为.
已知两个三角形相似,对应中线之比为1:4,那么对应周长之比为( )
A . 1:2
B . 1:16
C . 1:4
D . 无法确定
如果两个相似三角形对应边的比为2:3,那么这两个相似三角形面积的比是( )
A . 2:3
B .  :
:  C . 4:9
D . 8:27
C . 4:9
D . 8:27
 :
:  C . 4:9
D . 8:27
C . 4:9
D . 8:27
已知△ABC∽△A′B′C′,如果它们的相似比为3:2,那么它们的面积比应是( )
A . 3:2
B . 2:3
C . 4:9
D . 9:4
如图,在反比例函数y=  的图象上有一动点
的图象上有一动点  ,连接
,连接 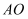 并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数
并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数  的图象上运动,
的图象上运动,  ,则关于
,则关于  的解为.
的解为.

两个相似三角形面积之比为2:7,较大三角形一边上的高为  ,则较小三角形的对应边上的高为.
,则较小三角形的对应边上的高为.
 ,则较小三角形的对应边上的高为.
,则较小三角形的对应边上的高为.
如图,矩形纸片ABCD中,AB=4,AD=3,折叠纸片使AD边与对角线BD重合,折痕为DG,记与点A重合的点为A′,则  A′BG的面积与该矩形面积的比为( )
A′BG的面积与该矩形面积的比为( )
 A′BG的面积与该矩形面积的比为( )
A′BG的面积与该矩形面积的比为( )
A . 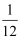 B .
B .  C .
C . 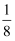 D .
D . 
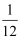 B .
B .  C .
C . 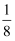 D .
D . 
如图,已知直线  与x轴相交于点A,与直线
与x轴相交于点A,与直线  相交于点P.动点E从原点O出发,以每秒2个单位的速度沿着O→P→A的路线向点A匀速运动,同时动点F从原点O出发,以每秒2个单位的速度沿着射线OA的方向运动,当点E到达终点A时点F随即停止运动,设运动时间为t秒,当动点E、F所在的直线将△OPA的面积分成1∶2的两部分时,t的值为。
相交于点P.动点E从原点O出发,以每秒2个单位的速度沿着O→P→A的路线向点A匀速运动,同时动点F从原点O出发,以每秒2个单位的速度沿着射线OA的方向运动,当点E到达终点A时点F随即停止运动,设运动时间为t秒,当动点E、F所在的直线将△OPA的面积分成1∶2的两部分时,t的值为。
 与x轴相交于点A,与直线
与x轴相交于点A,与直线  相交于点P.动点E从原点O出发,以每秒2个单位的速度沿着O→P→A的路线向点A匀速运动,同时动点F从原点O出发,以每秒2个单位的速度沿着射线OA的方向运动,当点E到达终点A时点F随即停止运动,设运动时间为t秒,当动点E、F所在的直线将△OPA的面积分成1∶2的两部分时,t的值为。
相交于点P.动点E从原点O出发,以每秒2个单位的速度沿着O→P→A的路线向点A匀速运动,同时动点F从原点O出发,以每秒2个单位的速度沿着射线OA的方向运动,当点E到达终点A时点F随即停止运动,设运动时间为t秒,当动点E、F所在的直线将△OPA的面积分成1∶2的两部分时,t的值为。 
已知:如图,⊙O和⊙A相交于C、D,圆心A在⊙O上,过A的直线与CD、⊙A、⊙O分别交于F、E、B。

求证:
-
(1) △AFC∽△ACB
-
(2)

如图,将菱形纸片ABCD折叠使点A恰好落在菱形的对称中心O处,折痕为EF,再次折叠图形,使点C恰好落在EF的中点G处,折痕为MN.若菱形ABCD的边长为2,∠A=120°,则MN的长度为( )

A . 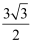 B . 2
C .
B . 2
C . 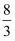 D .
D . 
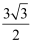 B . 2
C .
B . 2
C . 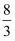 D .
D . 
如图,在平行四边形ABCD中,EF∥AB,DE:EA=2:3,EF=4,则CD的长为( )

A .  B . 8
C . 10
D . 16
B . 8
C . 10
D . 16
 B . 8
C . 10
D . 16
B . 8
C . 10
D . 16
如图,已知点A,点C在反比例函数y=  上(k>0,x>0)的图象上,AB⊥x轴于点B,连结OC交AB于点D,若CD=2OD,则△BDC与△ADO的面积比为( )
上(k>0,x>0)的图象上,AB⊥x轴于点B,连结OC交AB于点D,若CD=2OD,则△BDC与△ADO的面积比为( )
 上(k>0,x>0)的图象上,AB⊥x轴于点B,连结OC交AB于点D,若CD=2OD,则△BDC与△ADO的面积比为( )
上(k>0,x>0)的图象上,AB⊥x轴于点B,连结OC交AB于点D,若CD=2OD,则△BDC与△ADO的面积比为( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端在BC、CD上,若△ADE∽△CMN,求CM的长.

已知△ABC∽△DEF,若△ABC与△DEF的相似比为  ,则△ABC与△DEF对应中线的比为( )
,则△ABC与△DEF对应中线的比为( )
 ,则△ABC与△DEF对应中线的比为( )
,则△ABC与△DEF对应中线的比为( )
A .  B .
B .  C .
C . 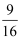 D .
D . 
 B .
B .  C .
C . 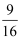 D .
D . 
已知  ,
,  的面积为6,周长为
的面积为6,周长为  周长的一半,则
周长的一半,则  的面积等于( )
的面积等于( )
 ,
,  的面积为6,周长为
的面积为6,周长为  周长的一半,则
周长的一半,则  的面积等于( )
的面积等于( )
A . 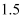 B .
B .  C .
C .  D .
D . 
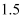 B .
B .  C .
C .  D .
D . 
要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为5cm,6cm和9cm,另一个三角形的最短边长为4cm,则它的最长边为( )
A . 4.8cm
B . 4cm
C . 4.5cm
D . 7.2cm
若相似三角形的相似比为1:4,则面积比为( )
A . 1:16
B . 16:1
C . 1:4
D . 1:2
如图所示,已知AD∥BC,∠ABC=90°,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC相似,则AP=.

最近更新
- 取一块金属钠,放在燃烧匙里加热,下列对实验现象的描述正确的是() ①金属先熔化 ②在空气中燃烧,产生黄色火花 ③燃烧后得
- 反比例函数(k≠0)的图象过点(2,-2),则此函数的图象在直角坐标系中的 A.第二、四象限 B.
- 单词辨认(共10题,每题1分,共10分)
- 下图是高中生物有关实验过程,其中操作和叙述正确的是A.①图甲是用低倍显微镜观察某视野中的图像,如要看清洋葱根尖细胞有丝分
- 25. The article is too long, please cut _____ some unimporta
- 不等式的解集是 。
- 假设你叫李华,在2008年暑假期间成为了北京奥运会的一名志愿者,请你用英语给美国的笔友Tom写一封100字左右的信,谈谈
- 风湿性心脏病、系统性红斑狼疮等一类疾病是 A.病原体感染机体而引发的疾病,有传染性
- 下列关于水的组成正确的说法是( ) A.由氢元素和氧元素组成 B.由氢气和氧气组成 C.由
- 根据句意及首字母,写出单词,使句子意思完整 1.My m________ birthday isDecember 13t
- 在“家电”身上似乎也可以看到人类自己的影子。依照下面示例的构想方式,写一段以“家电”讽喻人类的文字(写出两条)。 【示例
- 下列有关神经调节与体液调节的关系的叙述,错误的是( ) A.神经调节的作用时间短暂,体液调节的作用时间比较长 B.神经
- 阅读下面文言文,完成9-12题。朱晖字文季,南阳宛人也。晖早孤,年十三,王莽败,天下乱,与外氏家属从田闲奔入宛城。道遇群
- 甜菜根细胞的液泡中有花青素,使块根为红色。将块根切成小块放在蒸馏水中,水无明显的颜色变化,但用盐酸处理后再放人蒸馏水中,
- 太阳能热水器是把太阳能转化为内能的设备之一.某品牌太阳能热水器每小时平均接受4.2×106J的太阳能,在5小时的有效照射
- 下图为显微镜观察中的两个视野,其中细胞甲为主要观察对象,由视野(1)到视野(2)时,操作过程的正确顺序是 ①转
- (2012北京西城期末)如图所示,一单匝矩形金属线圈ABCD在匀强磁场中绕转轴OO匀速转动。转轴OO过AD边和BC边的中
- D......
- 某地位于45°S,150°E,有关该地的正确叙述是 A.西半球 B.北寒带 C.四季变化比较
- He is going to give a lecture, but when and where _____ yet.



