8 相似三角形的性质 知识点题库
如图,正方形ABCD中,M为BC上一点,且BM= BC.△AMN为等腰直角三角形,斜边AN与CD交于点F,延长AN与BC的延长线交于点E,连接MF、CN,作NG⊥BE,垂足为G,下列结论:①△ABM≌△MGN;②△CNG为等腰直角三角形;③MN=EN;④S△ABM=S△CEN;⑤BM+DF=MF.其中正确的个数为( )
BC.△AMN为等腰直角三角形,斜边AN与CD交于点F,延长AN与BC的延长线交于点E,连接MF、CN,作NG⊥BE,垂足为G,下列结论:①△ABM≌△MGN;②△CNG为等腰直角三角形;③MN=EN;④S△ABM=S△CEN;⑤BM+DF=MF.其中正确的个数为( )

A . 2个
B . 3个
C . 4个
D . 5个
若两个相似三角形的周长比为2:3,则它们的面积比是.
如图,Rt△ABC∽Rt△DEF , ∠A=35°,则∠E的度数为( ).

A . 35°
B . 45°
C . 55°
D . 65°
在Rt三角形ABC中,∠ACB=90°,∠A=30° CD⊥AB于点D,那么△ACD与△BCD的面积之比为.
在△ABC中,P为边AB上一点.

-
(1) 如图1,若∠ACP=∠B,求证:AC2=AP•AB;
-
(2) 若M为CP的中点,AC=2.
①如图2,若∠PBM=∠ACP,AB=3,求BP的长;
②如图3,若∠ABC=45°,∠A=∠BMP=60°,直接写出BP的长.
若△ABC∽△DEF,  =2,△ABC面积为8,则△DEF的面积为( )
=2,△ABC面积为8,则△DEF的面积为( )
 =2,△ABC面积为8,则△DEF的面积为( )
=2,△ABC面积为8,则△DEF的面积为( )
A . 1
B . 2
C . 4
D . 8
如图,  是等边三角形,点
是等边三角形,点  在同一条直线上,且
在同一条直线上,且  .
.
 是等边三角形,点
是等边三角形,点  在同一条直线上,且
在同一条直线上,且  .
.
-
(1) 请直接写出图中相似的三角形;
-
(2) 探究
 之间的关系,并说明理由.
之间的关系,并说明理由.
下列命题是真命题的是( )
A . 两直线平行,同位角相等
B . 相似三角形的面积比等于相似比
C . 菱形的对角线相等
D . 相等的两个角是对顶角
如图,△ABC的边BC在直线l上,AD是△ABC的高,∠ABC=45°,BC=6cm,AB=2  cm.点P从点B出发沿BC方向以1cm/s速度向点C运动,当点P到点C时,停止运动.PQ⊥BC,PQ交AB或AC于点Q,以PQ为一边向右侧作矩形PQRS,PS=2PQ.矩形PQRS与△ABC的重叠部分的面积为S(cm2),点P的运动时间为t(s).回答下列问题:
cm.点P从点B出发沿BC方向以1cm/s速度向点C运动,当点P到点C时,停止运动.PQ⊥BC,PQ交AB或AC于点Q,以PQ为一边向右侧作矩形PQRS,PS=2PQ.矩形PQRS与△ABC的重叠部分的面积为S(cm2),点P的运动时间为t(s).回答下列问题:
 cm.点P从点B出发沿BC方向以1cm/s速度向点C运动,当点P到点C时,停止运动.PQ⊥BC,PQ交AB或AC于点Q,以PQ为一边向右侧作矩形PQRS,PS=2PQ.矩形PQRS与△ABC的重叠部分的面积为S(cm2),点P的运动时间为t(s).回答下列问题:
cm.点P从点B出发沿BC方向以1cm/s速度向点C运动,当点P到点C时,停止运动.PQ⊥BC,PQ交AB或AC于点Q,以PQ为一边向右侧作矩形PQRS,PS=2PQ.矩形PQRS与△ABC的重叠部分的面积为S(cm2),点P的运动时间为t(s).回答下列问题:
-
(1) AD=cm;
-
(2) 当点R在边AC上时,求t的值;
-
(3) 求S与t之间的函数关系式.
在△ABC中,AB=9,AC=6.点M在边AB上,且AM=3,点N在AC边上.当AN=时,△AMN与原三角形相似.

如图,在矩形ABCD中,已知AB=24,BC=12,点E沿BC边从点B开始向点C以每秒2个单位长度的速度运动;点F沿CD边从点C开始向点D以每秒4个单位长度的速度运动,如果E、F同时出发,用t(0≤t≤6)秒表示运动的时间,当t为何值时,以点E、C、F为顶点的三角形与△ACD相似?

如图,点A在反比例函数y=- 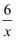 (x<0)的图象上,点B在反比例函数y=
(x<0)的图象上,点B在反比例函数y=  (x>0)的图象上,且∠AOB=90°.则tan∠OBA的值等于( )
(x>0)的图象上,且∠AOB=90°.则tan∠OBA的值等于( )
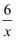 (x<0)的图象上,点B在反比例函数y=
(x<0)的图象上,点B在反比例函数y=  (x>0)的图象上,且∠AOB=90°.则tan∠OBA的值等于( )
(x>0)的图象上,且∠AOB=90°.则tan∠OBA的值等于( ) 
A . 2
B . 3
C .  D .
D . 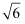
 D .
D . 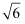
如图,在平面直角坐标系  中,
中,  三个顶点坐标分别为
三个顶点坐标分别为  ,
,  ,
,  .
.
 中,
中,  三个顶点坐标分别为
三个顶点坐标分别为  ,
,  ,
,  .
. 
-
(1) ①请画出
 关于
关于  轴对称的图形
轴对称的图形  ;
; ②将
 的三个顶点的横坐标与纵坐标同时乘
的三个顶点的横坐标与纵坐标同时乘 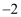 ,得到对应的点
,得到对应的点  、
、  、
、  ,请画出
,请画出 
 ;
; -
(2) 求
 与
与  的面积比,即
的面积比,即  :
:  =(不写解答过程,直接写出结果).
=(不写解答过程,直接写出结果).
若△ABC∽△DEF,相似比为5:4,则对应中线的比为( )
A . 5:4
B .  :2
C . 25:16
D . 16:25
:2
C . 25:16
D . 16:25
 :2
C . 25:16
D . 16:25
:2
C . 25:16
D . 16:25
如图,已知△ABC和点A'.

-
(1) 以点A'为顶点求作△A'B'C',使△A'B'C'∽△ABC,S△A'B'C'=4S△ABC.
(要求:尺规作图,保留作图痕迹,不写作法);
-
(2) 在(1)的条件下,若∠A=55°,∠B'=95°,求∠C.
如图,在平行四边形ABCD中,AD=BD=5,AB=6,E为AB的中点,F为CD上一点,连接EF交BD于点G , 若S△FDG:S△EDG=2:3,则EF的长是( )

A .  B . 2
B . 2  C . 2
C . 2 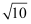 D . 5
D . 5
 B . 2
B . 2  C . 2
C . 2 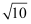 D . 5
D . 5
如图,方格纸中的每个小正方形的边长都是1,  是格点三角形(顶点在方格顶点处).
是格点三角形(顶点在方格顶点处).
 是格点三角形(顶点在方格顶点处).
是格点三角形(顶点在方格顶点处). 
-
(1) 在图1中画出一个格点
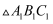 ,使得
,使得 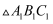 与
与  相似,周长之比为2:1;
相似,周长之比为2:1;
-
(2) 在图2中画出一个格点
 ,使得
,使得  与
与  相似,面积之比为2:1.
相似,面积之比为2:1.
如图,在平面直角坐标系中,抛物线  :
:  经过点
经过点  和
和  .
.
 :
:  经过点
经过点  和
和  .
. 
-
(1) 求抛物线
 的对称轴.
的对称轴.
-
(2) 当
 时,将抛物线
时,将抛物线  向左平移2个单位,再向下平移1个单位,得到抛物线
向左平移2个单位,再向下平移1个单位,得到抛物线  .
. ①求抛物线
 的解析式.
的解析式.②设抛物线
 与
与  轴交于
轴交于  ,
,  两点(点
两点(点  在点
在点  的右侧),与
的右侧),与  轴交于点
轴交于点  ,连接
,连接  .点
.点  为第一象限内抛物线
为第一象限内抛物线  上一动点,过点
上一动点,过点  作
作  于点
于点  .设点
.设点  的横坐标为
的横坐标为  .是否存在点
.是否存在点  ,使得以点
,使得以点  ,
,  ,
,  为顶点的三角形与
为顶点的三角形与  相似,若存在,求出
相似,若存在,求出  的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
如图,直线  分别交y轴、x轴于点A、B,其中
分别交y轴、x轴于点A、B,其中  、
、  的长是方程
的长是方程  的两根(
的两根(  ),将直线
),将直线  绕点O逆时针旋转
绕点O逆时针旋转 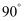 后与x轴、y轴分别交于点C、D,点P是该直线
后与x轴、y轴分别交于点C、D,点P是该直线  与双曲线在第一象限内的一个交点,
与双曲线在第一象限内的一个交点,  ⊥x轴于E,且
⊥x轴于E,且  .
.
 分别交y轴、x轴于点A、B,其中
分别交y轴、x轴于点A、B,其中  、
、  的长是方程
的长是方程  的两根(
的两根(  ),将直线
),将直线  绕点O逆时针旋转
绕点O逆时针旋转 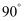 后与x轴、y轴分别交于点C、D,点P是该直线
后与x轴、y轴分别交于点C、D,点P是该直线  与双曲线在第一象限内的一个交点,
与双曲线在第一象限内的一个交点,  ⊥x轴于E,且
⊥x轴于E,且  .
. 
-
(1) 直线
 的解析式;
的解析式;
-
(2) 求点P的坐标;
-
(3) 设点Q与点P在同一个反比例函数的图象上,且点Q在直线
 的右侧,作
的右侧,作  ⊥x轴于点F,当
⊥x轴于点F,当  与
与  相似时,求点Q的横坐标.
相似时,求点Q的横坐标.
如图,已知在Rt△ABC中,∠ACB=90°,AC=8,BC=16,D是AC上的一点,CD=3,点P从B点出发沿射线BC方向以每秒2个单位的速度向右运动.设点P的运动时间为t秒,连接AP.

-
(1) 当t=3秒时,求AP的长度(结果保留根号);
-
(2) 填空:在运动过程中,当t=秒时,△ABP为等腰三角形;
-
(3) 过点D做DE⊥AP于点E.在点P的运动过程中,当t为何值时,能使DE=CD.
最近更新
- 某校化学兴趣小组同学发现,长期使用的热水壶底部有一层水垢,水垢的主要成分是碳酸钙和氢氧化镁。他们为了测定水垢中碳酸钙的含
- 一条弦把圆分为2∶3的两部分,那么这条弦所对的圆周角度数为
- 若圆锥侧面积为,高为,则其底面半径为 .
- 下列使用胶头滴管的操作方法正确的是
- The changes in computer will in the near future.
- 如图,在矩形ABCD中,AB=4,∠DCA=30°,点F是对角线AC上的一个动点,连接DF,以DF为斜边作∠DFE=30
- .一个三角形的3个外角的度数之比为2:3:4,则与之相应的3个内角的度数之比为( )A 4:3:2
- A元素的原子结构示意图为: A元素在化学反应中容易 电子变成________离子,属_____
- 基因型为AaBbCc的个体,测交后代的类型及比例是:Aabbcc占21%,AaBbCc占4%,AaBbcc占21%,Aa
- 如果让你担任历史纪实片《1911年的北京东交民巷》的导演,在反映当时的北京东交民巷时,不应该出现的画面是( )
- 在一密闭容器中,放入镍粉并充入一定量的CO气体,一定条件下发生可逆反应: Ni(s) + 4CO(g) Ni(CO)4
- 已知氯磺酸化学式为ClSO3H,能在水中完全电离出H+和ClSO3﹣;甲酸化学式为HCOOH,能在水中部分电离出H+和H
- 实数、在数轴上的位置如图3所示,则化简的结果为( )A.- B. C. D.
- 下列关于我国古代农耕经济基本特点的表述错误的是A以种植业为主、家畜饲养业为辅B精耕细作的生产模式 C刀耕火种、简单协作
- 小刚为探究“导体电阻大小与温度的关系”,选用不同型号的铅笔芯进行了如下实验:步骤一:将H型铅笔芯接入电路,闭合开关,测量
- 最新科技报道,美国夏威夷联合天文中心的科学家发现了新型氢粒子,这种新粒子是由3个氢原子核(只含质子)和2个电子构成的,对
- 江苏省连云港新海高级中学10-11学年高二上学期期中考试(历史· 无内容
- 某校历史学习小组要考察我国最早的原始人类生活的遗址,他们应该去( ) A.北京周口店 B.云
- 阅读下面的文字完成后面问题: 管仲的经济思想中,最为奇特的一项是鼓励消费,他甚至倡导奢侈,这在古往今来的治国者中可谓仅见
- 填入下文横线处的句子,与上下文衔接恰当的一项是 ( ) 海面上的巨浪猛烈地撞击着岸边的岩石。它那愤怒的咆哮声有时像



