8 相似三角形的性质 知识点题库
Rt△ABC的两条直角边分别为3 cm、4 cm,与它相似的Rt△A'B'C'的斜边为20 cm,那么Rt△A'B'C'的周长为( )
A . 48cm
B . 28cm
C . 12cm
D . 10cm
如图,E是正方形ABCD的边BC延长线上一点,且BC=CE,若CE=5cm,则CF的长为( )
A .  cm
B . 3cm
C .
cm
B . 3cm
C . 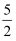 cm
D . 5cm
cm
D . 5cm
 cm
B . 3cm
C .
cm
B . 3cm
C . 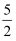 cm
D . 5cm
cm
D . 5cm
若△ABC∽△A′B′C′,∠A=40°,∠B=60°,则∠C′等于 ( )
A . 20°;
B . 40°;
C . 60°;
D . 80°.
两个相似三角形的面积比是9:16,则这两个三角形的相似比和周长的比分别为( )
A . 9:16;3:4
B . 3:4;9:16
C . 9:4;9:16
D . 3:4;3:4
如图,D为△ABC边AB上一点,且CD分△ABC为两个相似比为1: 的一对相似三角形;(不妨如图假设左小右大),求:
的一对相似三角形;(不妨如图假设左小右大),求:
 的一对相似三角形;(不妨如图假设左小右大),求:
的一对相似三角形;(不妨如图假设左小右大),求:(1)△BCD与△ACD的面积比;
(2)△ABC的各内角度数.

已知△ABC∽△DEF,△ABC的周长为1,△DEF的周长为3,则△ABC与△DEF的面积之比为.
如图,△ABC中,D为BC 上一点,∠BAD=∠C,AB=6, BD=4,求CD的长.

如图,在平行四边形ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使△CBF∽△CDE,则BF的长是( )

A . 5
B . 8.2
C . 6.4
D . 1.8
如图,平行于BC的直线DE把△ABC分成面积相等的两部分,则  的值为( )
的值为( )
 的值为( )
的值为( ) 
A . 1
B .  C .
C .  D .
D . 
已知:如图,在  中,
中,  ,
,  ,
, 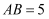 ,
,  是斜边
是斜边  的中点,以
的中点,以  为顶点,作
为顶点,作  ,
,  的两边交边
的两边交边  于点
于点  、
、  (点
(点  不与点
不与点  重合)
重合)
 中,
中,  ,
,  ,
, 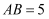 ,
,  是斜边
是斜边  的中点,以
的中点,以  为顶点,作
为顶点,作  ,
,  的两边交边
的两边交边  于点
于点  、
、  (点
(点  不与点
不与点  重合)
重合) 
-
(1) 当
 时,求
时,求 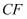 的长度;
的长度;
-
(2) 当
 绕点
绕点  转动时,设
转动时,设  ,
,  ,求
,求  关于
关于  的函数解析式,并写出
的函数解析式,并写出  的取值范围.
的取值范围.
-
(3) 联结
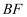 ,是否存在点
,是否存在点  ,使△
,使△  与△
与△  相似?若存在,请求出此时
相似?若存在,请求出此时 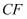 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.
如图1,△ABC内接于圆O,连接AO,延长AO交BC于点D,AD⊥BC.

-
(1) 求证:AB=AC;
-
(2) 如图2,在圆O上取一点E,连接BE、CE,过点A作AF⊥BE于点F,求证:EF+CE=BF;
-
(3) 如图3在(2)的条件下,在BE上取一点G,连接AG、CG,若
 ∠AGB+∠ABC=90°,∠AGC=∠BGC,AG=6,BG=5,求EF的长.
∠AGB+∠ABC=90°,∠AGC=∠BGC,AG=6,BG=5,求EF的长.
如图,已知等边三角形  中,点
中,点  分别在边
分别在边  上,把
上,把  沿直线
沿直线  翻折使点
翻折使点  落在
落在 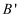 处,
处,  、
、  分别交边
分别交边  于点
于点  、
、  ,若
,若  ,则
,则  度数为.
度数为.
 中,点
中,点  分别在边
分别在边  上,把
上,把  沿直线
沿直线  翻折使点
翻折使点  落在
落在 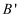 处,
处,  、
、  分别交边
分别交边  于点
于点  、
、  ,若
,若  ,则
,则  度数为.
度数为. 
如图,  中,
中,  是
是 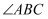 的平分线,
的平分线, 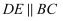 ,
,  ,
,  ,求
,求  的长.
的长.
 中,
中,  是
是 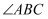 的平分线,
的平分线, 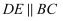 ,
,  ,
,  ,求
,求  的长.
的长. 
若  ,且面积比为
,且面积比为  ,则其对应边上的高的比( )
,则其对应边上的高的比( )
 ,且面积比为
,且面积比为  ,则其对应边上的高的比( )
,则其对应边上的高的比( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,抛物线  与
与  轴交于A、B(3,0)两点,与
轴交于A、B(3,0)两点,与  轴交于点C(0,-3),抛物线的顶点为D.
轴交于点C(0,-3),抛物线的顶点为D.
 与
与  轴交于A、B(3,0)两点,与
轴交于A、B(3,0)两点,与  轴交于点C(0,-3),抛物线的顶点为D.
轴交于点C(0,-3),抛物线的顶点为D. 
-
(1) 求抛物线的解析式;
-
(2) 点P在抛物线的对称轴上,点Q在
 轴上,若以点P、Q、B、C为顶点,BC为边的四边形为平行四边形,请直接写出点P、Q的坐标;
轴上,若以点P、Q、B、C为顶点,BC为边的四边形为平行四边形,请直接写出点P、Q的坐标;
-
(3) 已知点M是
 轴上的动点,过点M作
轴上的动点,过点M作  的垂线交抛物线于点G,是否存在这样的点M,使得以点A、M、G为顶点的三角形与△BCD相似,若存在,请求出点M的坐标;若不存在,请说明理由.
的垂线交抛物线于点G,是否存在这样的点M,使得以点A、M、G为顶点的三角形与△BCD相似,若存在,请求出点M的坐标;若不存在,请说明理由.
已知△ABC与ΔA'B'C'相似,并且点A与点A'、点B与点B'、点C与点C'是对应顶点,其中∠A=80°,∠B'=60°,则∠C=度.
△ABC中,AB=6,BC=10,CA=12,另一个和它相似的三角形最长的一边是36,则最短的一边是( )
A . 12
B . 18
C . 20
D . 27
如图所示,在△ABC中,AB=8,AC=6,P是AC的中点,过 P点的直线交 AB于点Q,若以A、P、Q为顶点的三角形和以A、B、C为顶点的三角形相似,则AQ的长为.

已知  ,且相似比为
,且相似比为 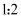 ,则
,则  与
与  的周长比为( )
的周长比为( )
 ,且相似比为
,且相似比为 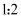 ,则
,则  与
与  的周长比为( )
的周长比为( )
A .  B .
B .  C .
C . 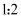 D .
D . 
 B .
B .  C .
C . 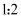 D .
D . 
已知 ∽
∽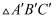 ,
,  和
和 是它们的对应角平分线,若
是它们的对应角平分线,若 ,
,  , 则
, 则 与
与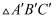 的面积比是( )
的面积比是( )
 ∽
∽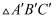 ,
,  和
和 是它们的对应角平分线,若
是它们的对应角平分线,若 ,
,  , 则
, 则 与
与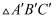 的面积比是( )
的面积比是( )
A .  :
: B .
B .  :
: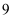 C .
C .  :
: D .
D . 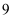 ;
;
 :
: B .
B .  :
: C .
C .  :
: D .
D . 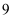 ;
;
最近更新
- 关于闭合电路,下列说法中正确的是:A.电源短路时,放电电流为无限大 B.电源短路时,内电压等于电源电动势C.用电
- 东突恐怖势力企图分裂新疆的行径不得人心。下列史实中最能充分说明新疆地区是我国不可分割的一部分的是 A.张骞出使西域
- 思念亲友,我们曾如岑参“故园东望路漫漫,___________________”;也曾如李白“此夜曲中闻折柳,_____
- ——What do you think made Mary so upset? —— ______ her new MP
- 小黄患急性炎症到医院就医,通过验血发现其血液中 A.白细胞增多 B.红细胞增多 C.血小
- 25.下列细胞中最可能为浆细胞的是
- --- Zhao Rui, it’s said that many famous singers will come t
- 用词的引申意义造句。 例:五千年的古国文化,从你这儿发源。 澎湃—— 扮演——
- 我家有女初长成 尤今 在上海的一家餐馆里。 负责为我们上菜的那位女侍,年轻得像是树上的一片嫩叶。
- 三峡水利枢纽工程是长江流域治理开发的关键工程,建成后将是中国规模最大的水利工程。枢纽控制流域面积1.0×106km2,占
- 从下面这则材料中提炼一个论点。 有关人士指出,诺贝尔奖一直是我们的一个心痛,我们呼唤了那么多年,为什么呼唤
- 下列关于氧气(O2)的说法不科学的是() A、常用带火星的木条来检验空气中的O2 B、硫在O2里燃烧产生明
- 思想高尚的人,不会做偷鸡摸狗之事;思想龌龊的人,不可能成就惊天动地的事业。播种一种观念就收获一种行为,播种一种行为就收获
- 锂离子电池已经成为第一代实用化的蓄电池,该电池具有能量密度大、电压高的特性.锂离子电池放电时的电极反应式为: 负极反应:
- 在我国古代著名的数学专著《九章算术》里有—段叙述:今有良马与驽马发长安至齐,齐去长 安一千一百二十五里,良马初日行一百零
- 两物块A、B用轻弹簧相连,质量均为2 kg,初始时弹簧处于原长,A、B两物块都以v=6 m/s的速度在光滑的水平地面上运
- (三)阅读下面一段文言文,完成13~16题。(每小题3分,共12分) 潘荣,字尊用,龙溪人。正统十三年进士。犒师广东,还
- 沟通两大洋,连结两大洲的海峡是 ( ) A.马六甲海峡 B.英吉利海峡
- Nobody could______it when the bull broke into the shop and a
- 在进行英语听力测试时,各考场的有线扬声器是同时开播,也是同时停播的.它们的连接方式是______联,原因是它们_____



