8 相似三角形的性质 知识点题库
如图,在△ABC中,AB=AC=2,∠BAC=20°.动点P、Q分别在直线BC上运动,且始终保持∠PAQ=100°.设BP=x,CQ=y,则y与x之间的函数关系用图象大致可以表示为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若两个相似三角形的面积比为4:1,那么这两个三角形的对应边的比为( )
A . 4:1
B . 1:4
C . 2:1
D . 16:1
已知:如图,D是BC上一点,△ABC∽△ADE,求证:∠1=∠2=∠3.

如图,矩形ABCD中,AB=3,AD=4,E为AB上一点,AE=1,M为射线AD上一动点,AM=a(a为大于0的常数),直线EM与直线CD交于点F,过点M作MG⊥EM,交直线BC于点G.

-
(1) 若M为边AD中点,求证△EFG是等腰三角形;
-
(2) 若点G与点C重合,求线段MG的长;
-
(3) 请用含a的代数式表示△EFG的面积S,并指出S的最小整数值.
已知△ABC中,D为AB边上任意一点,DF∥AC交BC于F,AE∥BC,∠CDE=∠ABC=∠ACB=α.
-
(1)
如图1,当α=60°时,求证:△DCE是等边三角形;

-
(2)
如图2,当α=45°时,求证:①
 =
=  ;②CE⊥DE.
;②CE⊥DE.
-
(3)
如图3,当α为任意锐角时,请直接写出线段CE与DE的数量关系是:
 =.
=.
如图,矩形OABC的两边在坐标轴上,点A的坐标为(10,0),抛物线y=ax2+bx+4过点B,C两点,且与x轴的一个交点为D(﹣2,0),点P是线段CB上的动点,设CP=t(0<t<10).

-
(1) 请直接写出B、C两点的坐标及抛物线的解析式;
-
(2) 过点P作PE⊥BC,交抛物线于点E,连接BE,当t为何值时,∠PBE=∠OCD?
-
(3) 点Q是x轴上的动点,过点P作PM∥BQ,交CQ于点M,作PN∥CQ,交BQ于点N,当四边形PMQN为正方形时,请求出t的值.
若相似△ABC与△DEF的相似比为1:3,则△ABC与△DEF的面积比为( )
A . 1:3
B . 1:9
C . 3:1
D . 1: 

在△ABC中,E是AB上一点,AE=2,BE=3,AC=4,在AC上取一点D,使△ADE与△ABC相似,则AD的长为.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.

-
(1) 求证:∠DAF=∠CDE;
-
(2) 求证:△ADF∽△DEC;
-
(3) 若AE=6,AD=8,AB=7,求AF的长.
如图,在平面直角坐标系中,矩形OABC的两边分别在x轴和y轴上,OA=10厘米,OC=6厘米,现有两动点P,Q分别从O,A同时出发,点P在线段OA上沿OA方向作匀速运动,点Q在线段AB上沿AB方向作匀速运动,已知点P的运动速度为1厘米/秒.

-
(1) 设点Q的运动速度为0.5厘米/秒,运动时间为t秒,
①当△CPQ的面积最小时,求点Q的坐标;
②当△COP和△PAQ相似时,求点Q的坐标.
-
(2) 设点Q的运动速度为a厘米/秒,问是否存在a的值,使得△OCP∽△PAQ∽CBQ?若存在,请求出a的值,并写出此时点Q的坐标;若不存在,请说明理由.
如图1,已知在平面直角坐标系中,点O为坐标原点,点A在  轴负半轴上,直线
轴负半轴上,直线  与
与  轴、
轴、  轴分别交于B、C两点,四边形ABCD为平行四边形,且AC=BC,点P为△ACD内一点,连接AP、BP且∠APB=90°.
轴分别交于B、C两点,四边形ABCD为平行四边形,且AC=BC,点P为△ACD内一点,连接AP、BP且∠APB=90°.
 轴负半轴上,直线
轴负半轴上,直线  与
与  轴、
轴、  轴分别交于B、C两点,四边形ABCD为平行四边形,且AC=BC,点P为△ACD内一点,连接AP、BP且∠APB=90°.
轴分别交于B、C两点,四边形ABCD为平行四边形,且AC=BC,点P为△ACD内一点,连接AP、BP且∠APB=90°. 
-
(1) 求证:∠PAC=∠PBC;
-
(2) 如图2,点E在线段BP上,点F在线段AP上,且AF=BE,∠AEF=45°,求
 的值;
的值;
-
(3) 在(2)的条件下,当PE=BE时,求点P的坐标.
如图,△ABC与△A'B'C'是位似图形,点O是位似中心,若OA=2AA',S△ABC=8,则S△A'B'C'=.

两相似三角形的相似比为  ,它们的面积之差为15,则面积之和是( )
,它们的面积之差为15,则面积之和是( )
 ,它们的面积之差为15,则面积之和是( )
,它们的面积之差为15,则面积之和是( )
A . 39
B . 75
C . 76
D . 40
如图中两三角形相似,则x=.

如图,△ABC与△DEF位似,位似中心为点O,且BC:EF=3:2,则S△ABC:S△DEF=.

泰勒斯是古希腊时期的思想家,科学家,哲学家,他最早提出了命题的证明.泰勒斯曾通过测量同一时刻标杆的影长,标杆的高度。金字塔的影长,推算出金字塔的高度。这种测量原理,就是我们所学的( )

A . 图形的平移
B . 图形的旋转
C . 图形的轴对称
D . 图形的相似
要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为4厘米,6厘米和9厘米,另一个三角形的最长边是18厘米,则它的最短边是( )
A . 2厘米
B . 4厘米
C . 8厘米
D . 12厘米
若两个相似三角形的面积之比为1∶9,则它们对应角平分线之比为( )
A .  B . 3
C .
B . 3
C .  D .
D . 
 B . 3
C .
B . 3
C .  D .
D . 
已知△ABC∽△A′B′C′,AD和A′D′是对应高,且AD:A′D′=2,则△ABC与△A′B′C′的周长比是.
如图,在平面直角坐标系中,△ABC与△DEF是以坐标原点O为位似中心的位似图形,若A(﹣2,0),D(3,0),且BC=3,则线段EF的长度为( )

A . 2
B . 4
C . 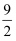 D . 6
D . 6
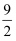 D . 6
D . 6
最近更新
- 在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图1所示 若将运动员按成绩由好到差编为1-35号,再用
- 下列说法中,正确的是 A.日用铝制品表面覆盖着氧化膜,对内部金属起保护作用 B.钢铁设备与外加直流电源的正极相连
- 等差数列{an},a1,a2025是的极值点,则=( ) A.2 B.3 C.4 D.5
- 写出从五个元素a、b、c、d、e中任取三个元素的所有组合,并求出其组合数.
- You be hungry;you had a big cake only an hour ago.
- 函数的图像关于直线对称,则= ▲
- 人体内物质的运输主要依靠 A.运动系统 B.泌尿系统 C.血液循环系统
- 下列关于遗嘱继承的说法正确的是 ①它是我国公民实现遗产继承的唯一方式②它不受继承顺序的限制,被继承人为保证遗嘱的视线,可
- “马克思说过,科学技术是生产力,事实证明这讲得很对。依我看,科学技术是第一生产力。”最能体现这一说法的是 A.“铁人”王
- (2006四川高考理综,4 )用基因工程技术可使大肠杆菌合成人的蛋白质。下列叙述不正确的是() A.常用相同的限制性内
- 下列图形中不是轴对称图形的是( ).
- 园艺师能将一株仙人掌培育成具有多种形状、开多种颜色花朵的仙人掌类植物,能达到上述目的的技术是( ) A.组织培养
- 下列实验操作正确的是( )
- 下列各图所示变化中属于化学变化的是( ) A. 对玻璃片呼气 B. 蜡烛燃烧 C. 湿衣晾干
- 阅读下面三句话,按要求回答问题。 ①柏拉图说:“征服自己需要更大的勇气,其胜利也是所有胜利中最光荣的胜利。” ②卢梭则谈
- ---- Are these _______ bags? ---- Yes, ______ ar
- 美国历史学家费正清在《伟大的中国革命》一书中表达了这样的观点:“鸦片战争的发生意味着中国拒绝在外交平等和对等贸易的基础上
- 生物膜在结构和功能上具有一定的联系。高尔基体具有极性,靠近细胞核的一面称为形成面,接近细胞膜的一面称为成熟面。从形成面到
- (1) 念天地之悠悠,___________________!(陈子昂《登幽州台歌》)(2)______________
- 《清平乐.村居》最能表现童真、童趣的句子是 ,



