九年级(初三)数学下学期下册试题
如图,在⊙O中,弦AB的长为 , 圆心到弦AB的距离为1,则∠BOC的度数为.
, 圆心到弦AB的距离为1,则∠BOC的度数为.
 , 圆心到弦AB的距离为1,则∠BOC的度数为.
, 圆心到弦AB的距离为1,则∠BOC的度数为.

如图, 是
是 的直径,
的直径,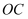 是半径,连接
是半径,连接 ,
,  . 延长
. 延长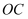 至点
至点 , 使
, 使 , 过点
, 过点 作
作 交
交 的延长线于点
的延长线于点 .
.
 是
是 的直径,
的直径,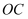 是半径,连接
是半径,连接 ,
,  . 延长
. 延长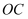 至点
至点 , 使
, 使 , 过点
, 过点 作
作 交
交 的延长线于点
的延长线于点 .
. 
-
(1) 求证:
 是
是 的切线;
的切线;
-
(2) 若
 ,
,  , 求
, 求 半径的长.
半径的长.
由若干个相同的小正方体搭成的一个几何体的俯视图如图所示,小正方形中的数字表示该位置的小正方体的个数,则这个几何体的主视图是( )

A .  B .
B .  C .
C .  D .
D . 
 C .
C . 如图,是由一些相同的小正方体搭成的几何体的三视图,搭成这个几何体的小正方体的个数有( )
A . 2个
B . 3个
C . 4个
D . 6个
在研究相似问题时,甲、乙同学的观点如下:

对于两人的观点,下列说法正确的是( )
A . 两人都对
B . 两人都不对
C . 甲对,乙不对
D . 甲不对,乙对
如图,在平面直角坐标系xOy中,双曲线y=  与直线y=﹣2x+2交于点A(﹣1,a).
与直线y=﹣2x+2交于点A(﹣1,a).
 与直线y=﹣2x+2交于点A(﹣1,a).
与直线y=﹣2x+2交于点A(﹣1,a).
-
(1) 求a,m的值;
-
(2) 求该双曲线与直线y=﹣2x+2另一个交点B的坐标.
下图是由4个相同的小正方体组成的立体图形,这个立体图形的主视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,点  在
在  轴正半轴上,点
轴正半轴上,点  是反比例函数图象上的一点,且
是反比例函数图象上的一点,且  .过点
.过点  作
作  轴交反比例函数图象于点
轴交反比例函数图象于点  .
.
 在
在  轴正半轴上,点
轴正半轴上,点  是反比例函数图象上的一点,且
是反比例函数图象上的一点,且  .过点
.过点  作
作  轴交反比例函数图象于点
轴交反比例函数图象于点  .
. 
-
(1) 求反比例函数的表达式;
-
(2) 求点
 的坐标.
的坐标.
已知点P(1,-3)在反比例函数y=  (k≠0)的图象上,则k的值是( )
(k≠0)的图象上,则k的值是( )
 (k≠0)的图象上,则k的值是( )
(k≠0)的图象上,则k的值是( )
A . 3
B . -3
C .  D .
D . 
 D .
D . 
在相同时刻的物高与影长成比例,如果高为1.5米的测竿的影长为3米,那么影长为30米的旗杆的高是 ( )
A . 20米
B . 18米
C . 16米
D . 15米
已知△ABC在平面直角坐标系中的位置如图所示.
(1)将△ABC绕圆点O旋转180°得到△A1B1C1 , 请你在图中画出△A1B1C1;
(2)写出点A1的坐标;
(3)求△A1B1C1的面积.
如图所示,在平面直角坐标系xOy中,在直线x=1处放置反光镜Ⅰ,在y轴处放置一个需开缺口的挡板Ⅱ,缺口为线段AB,其中点A(0,1),点B在点A上方,在直线x=﹣2处放置一个挡板Ⅲ,从点O发出的光线经反光镜Ⅰ反射后,通过缺口AB照射在挡板Ⅲ上,若需在挡板Ⅲ形成长度为2的光线,则在挡板Ⅱ需开缺口AB的长度为.

如图所示,在天水至宝鸡(天宝)高速公路建设中需要确定某条隧道AB的长度,已知在离地面2700米高度C处的飞机上,测量人员测得正前方AB两点处的俯角分别是60°和30°,求隧道AB的长.(结果保留根号)

如图,在△ABC中,点D在BC边上,连接AD,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是( )

A .  =
=  B .
B .  =
=  C .
C .  =
=  D .
D .  =
= 
 =
=  B .
B .  =
=  C .
C .  =
=  D .
D .  =
= 
如图,已知在平面直角坐标系中,  是坐标原点,点
是坐标原点,点  在反比例函数
在反比例函数  的图象上.一次函数
的图象上.一次函数  的图象经过点
的图象经过点  ,且与反比例函数图象的另一交点为
,且与反比例函数图象的另一交点为  .
.
 是坐标原点,点
是坐标原点,点  在反比例函数
在反比例函数  的图象上.一次函数
的图象上.一次函数  的图象经过点
的图象经过点  ,且与反比例函数图象的另一交点为
,且与反比例函数图象的另一交点为  .
. 
-
(1) 求反比例函数和一次函数的解析式;
-
(2) 根据图象直接写出
 时,
时,  的取值范围.
的取值范围.
下列图象中是反比例函数y=﹣ 图象的是( )
图象的是( )
 图象的是( )
图象的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
解方程或计算化简:
-
(1) 解方程:x2+6x=0
-
(2) 计算化简:(
 )﹣2﹣8cos60°﹣(
)﹣2﹣8cos60°﹣(  )0
)0
计算:(﹣1)2019  sin60°﹣(﹣3).
sin60°﹣(﹣3).
 sin60°﹣(﹣3).
sin60°﹣(﹣3).
一个高为8cm的圆柱,如果它的高增加3cm,那么它的表面积就增加18.84cm2 , 原圆柱的体积是().
已知反比例函数y=  的图象的一支位于第一象限.
的图象的一支位于第一象限.
 的图象的一支位于第一象限.
的图象的一支位于第一象限. 
-
(1) 判断该函数图象的另一支所在的象限,并求m的取值范围;
-
(2) 如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,若△OAB的面积为6,求m的值.
最近更新
- 正九边形的一个外角等于 .
- 在复平面内,复数(是虚数单位)对应的点位于 ( ) A.第一象限 B.第二象限 C.第三象限 D.
- —Have children eaten anything? —Yes. __________had a b
- 若曲线:与曲线:有四个不同的交点,则实数m的取值范围是 A.(,) B.(,0)∪(0,)
- “低碳生活”是指生活作息时所耗用的能量要尽量少,减低二氧化碳排放量,保护环境。下列做法符合“低碳生活”理念的是A.节约
- 如图所示,两线圈绕在同一软铁芯的两端并组成水平放置的光滑导轨,两金属棒PQ、MN可自由移动.当PQ在外力作用下运动时,M
- 下列关于纬线和纬度的叙述中,正确的是
- 已知函数满足,当时,,则( ) A.或 B.或 C
- 有相同条件下的三个反应:①2A-+B2 = 2B-+A2 ②2C-+A2 = 2A-+C2 ③2B-+D2 = 2D-
- 我国境内的远古人类已自觉或不自觉地使用多种能源,下列哪种能源是他们不曾使用的 () A.天然风
- 如图,在矩形ABCD中,AB=m(m是大于0的常数),BC=8,E为线段BC上的动点(不与B、C重合).连结DE,作EF
- 维也纳中国新春音乐会于2007年2月3日在奥地利维也纳的金色大厅举行,中国京剧与西方的交响乐交相辉映。中国艺术团选择京剧
- 若抛物线的焦点与椭圆的上焦点重合, 1)求抛物线方程. 2)若是过抛物线焦点的动弦,直线是抛物线两条分别切于的切线,求的
- 孟德尔的两对相对性状的遗传实验中,具有l:1:l:l比例的是. ①Fl产生配子类型的比例②F2表现型的比例③Fl
- 下列事件,使华盛顿体系受到巨大冲击的是 ( )A.国民政府发起改订新约运动
- “立子以嫡不以长,立嫡以长不以贤”(《春秋·公羊传》),这句话反映了西周时期的 A.禅让制 B.分封
- I spoke that slowly but I didn’t __________my meaning ______
- 下列句中加点词的古今意义相同的一项是 A.乃封甘罗,以为上卿 B.今者张唐欲称疾不肯行 C.左右欲刃相如 D.去咸阳七里
- 如图是我市新宁崀山八角寨美景:峰峦浓雾缭绕,若隐若现,令人心旷神怡。其中雾的形成是 A.汽化现象 B.
- 下列说法正确的是



