九年级(初三)数学下学期下册试题
已知反比例函数  的图象经过点(2,-2),则k的值为
的图象经过点(2,-2),则k的值为
 的图象经过点(2,-2),则k的值为
的图象经过点(2,-2),则k的值为
A . 4
B .  C . -4
D . -2
C . -4
D . -2
 C . -4
D . -2
C . -4
D . -2
小聪设计奖杯,从抛物线形状上获得灵感,在平面直角坐标系中画出截面示意图,如图1,杯体ACB是抛物线的一部分,抛物线的顶点C在y轴上,杯口直径 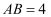 ,且点A,B关于y轴对称,杯脚高
,且点A,B关于y轴对称,杯脚高  ,杯高
,杯高  ,杯底MN在x轴上.
,杯底MN在x轴上.
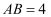 ,且点A,B关于y轴对称,杯脚高
,且点A,B关于y轴对称,杯脚高  ,杯高
,杯高  ,杯底MN在x轴上.
,杯底MN在x轴上.

-
(1) 求杯体ACB所在抛物线的函数表达式(不必写出x的取值范围).
-
(2) 为使奖杯更加美观,小敏提出了改进方案,如图2,杯体
 所在抛物线形状不变,杯口直径
所在抛物线形状不变,杯口直径  ,杯脚高CO不变,杯深
,杯脚高CO不变,杯深  与杯高
与杯高  之比为0.6,求
之比为0.6,求  的长.
的长.
如图,AD与BC相交于E,点F在BD上,且AB∥EF∥CD,若EF=2,CD=3,则AB的长为.

如右图所示的工件的主视图是( )

A .  B .
B .  C .
C .  D .
D . 
阜阳文峰塔,位于安徽阜阳城中心干道颍州路附近,于康熙三十五年(1796)建文峰塔,以振兴阜阳文风,小王在A处测得塔顶D的仰角为60°,在B处测得塔顶D的仰角为45°,其中A、C两点分别位于B、D两点正下方,且A、C两点在同一水平线上,已知AB高为13.5米,求中江塔CD的高度.(结果精确到个位)

如图,在平面直角坐标系中,点A在第二象限内,点B在x轴上,∠AOB=30°,AB=BO,反比例函数y=  (x<0)的图象经过点A,若S△ABO=
(x<0)的图象经过点A,若S△ABO=  ,则k的值为.
,则k的值为.
 (x<0)的图象经过点A,若S△ABO=
(x<0)的图象经过点A,若S△ABO=  ,则k的值为.
,则k的值为. 
计算:
-
(1)
 cos30°+
cos30°+  sin45°;
sin45°;
-
(2) 6tan230°﹣
 sin 60°﹣2sin 45°.
sin 60°﹣2sin 45°.
先化简,再求代数式  的值,其中x=cos30°.
的值,其中x=cos30°.
 的值,其中x=cos30°.
的值,其中x=cos30°.
当棱长为20的正方体的某个面平行于投影面时,这个面的正投影的面积为( )
A . 20
B . 300
C . 400
D . 600
下列函数中,y关于x的反比例函数是( )
A . x(y+2)=1
B . y= 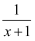 C . y=
C . y=  D . y=﹣
D . y=﹣ 
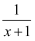 C . y=
C . y=  D . y=﹣
D . y=﹣ 
已知反比例函数y=  (k≠0)的图象经过点(﹣2,8).求这个反比例函数的解析式.
(k≠0)的图象经过点(﹣2,8).求这个反比例函数的解析式.
 (k≠0)的图象经过点(﹣2,8).求这个反比例函数的解析式.
(k≠0)的图象经过点(﹣2,8).求这个反比例函数的解析式.
计算:  ﹣cos45°+(1﹣
﹣cos45°+(1﹣  )2 .
)2 .
 ﹣cos45°+(1﹣
﹣cos45°+(1﹣  )2 .
)2 .
某工厂现有原材料100吨,每天平均用去x吨,这批原材料能用y天,则y与x之间的函数表达式为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图所示,课外活动中,小明在离旗杆AB的10米C处,用测角仪测得旗杆顶部A的仰角  ,已知测角仪器的高CD=1. 5米,求旗杆AB的高.(精确到0.1米)(供选用的数据:
,已知测角仪器的高CD=1. 5米,求旗杆AB的高.(精确到0.1米)(供选用的数据:  ,
,  ,
,  )
)
 ,已知测角仪器的高CD=1. 5米,求旗杆AB的高.(精确到0.1米)(供选用的数据:
,已知测角仪器的高CD=1. 5米,求旗杆AB的高.(精确到0.1米)(供选用的数据:  ,
,  ,
,  )
) 
在下列的四个几何体中,同一几何体的主视图与俯视图相同的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如果矩形的面积为6cm2 , 那么它的长ycm与宽xcm之间的函数图象大致为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图所示,已知  为反比例函数
为反比例函数 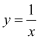 图象上的两点,动点
图象上的两点,动点  在
在  轴正半轴上运动,当
轴正半轴上运动,当  的值最大时,连结
的值最大时,连结  ,
,  的面积是 ( )
的面积是 ( )
 为反比例函数
为反比例函数 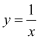 图象上的两点,动点
图象上的两点,动点  在
在  轴正半轴上运动,当
轴正半轴上运动,当  的值最大时,连结
的值最大时,连结  ,
,  的面积是 ( )
的面积是 ( ) 
A .  B . 1
C .
B . 1
C .  D .
D . 
 B . 1
C .
B . 1
C .  D .
D . 
下列各组中的四条线段是成比例线段的是( )
A . 4cm,4cm,5cm,6cm
B . 1cm,2cm,3cm,5cm
C . 3cm,4cm,5cm,6cm
D . 1cm,2cm,2cm,4cm
胜利塔是某市标志性建筑物之一,如图,为了测得胜利塔的高度AB,在D处用高度为1.3 m的测角仪CD测得胜利塔的顶端A的仰角为30°,再前进113 m到达F处,又测得胜利塔的顶端A的仰角为60°,求胜利塔的高度AB.(  ≈1.73,结果精确到0.1m)
≈1.73,结果精确到0.1m)
 ≈1.73,结果精确到0.1m)
≈1.73,结果精确到0.1m) 
如图,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东20°方向,然后向西走35米到达C点,测得点B在点C的北偏东45°方向.

-
(1) 求
 的度数;
的度数;
-
(2) 求这段河的宽度约为多少米.
(参考数据:
 ,
,  ,
,  )
)
最近更新
- 关于原子、分子的说法中,错误的是() A.分子、原子都能直接构成物质 B.分子是保持物质化学性质的最小粒子 C.原子的质
- A group of soldiers were watched ________ toward to the fron
- 某学校研究小组利用叶面积相等的A、B两种植物的叶片分别进行了以下两组实验(假设两组实验在相同且适宜的温度下进行,忽略光照
- He _____ his engagement justbefore the wedding. A. br
- 实验是学习自然科学最有效方法。化学实验中常常会出现意外情况,这是提升我们学科素养的良好机会,要根据具体情况区别对待,善于
- 函数是定义在R上的奇函数,并且当时,,那么,= .
- A Narrow Escape Shortly after the war, my brother and I were
- The rainbow _____ as the sun came fully out from behind the
- 有一无色未知溶液中检验出有Ba2+、Ag+,同时又测得其酸性很强。下列离子中,还需要作进一步的化学实验才能确定是否大量存
- 氨气溶于水得到氨水,氯气溶于水得到氯水,下列关于新制的氨水、氯水的描述正确的是
- (07年湖北卷理)(12分)如图,在三棱锥中,底面,,是的中点,且,.(I)求证:平面;(II)当角变化时,求直线与平面
- They look forward ________ a chance to receivefurther educat
- 现有一个标有“6V,0.5A”的小灯泡,但只有一个电压为10V的电源,为使小灯泡正常发光,应 联接一个
- 已知函数f(x)=ax3+3x2-x+1,问是否存在实数a,使得f(x)在(0,4)上单调递减?若存在,求出a的范围;若
- 阅读下列一段文字,完成(1)-(4)题。 成长的历程镌刻着太多的怀想,红了樱桃,绿了芭蕉。在月光似水的夜晚,我们静听心灵
- 在南方谈话中指出“社会主义要赢得与资本主义相比较的优势,就必须大胆吸收和借鉴人类社会创造的一切文明成果。”在这一思想指导
- 右图为某细胞结构示意图,下列选项中的变化都会在该细胞中发生的是()A.氨基酸→胰岛素;ATP→ADP+Pi B.氨基酸→
- -3+(—1)÷+(—5)
- 如图所示,将带电棒移近两个不带电的导体球,两个导体球开始时互相接触且对地绝缘,下述几种方法中能使两球都带电的是
- 写出一个过点(0,3),且函数值y随自变量x的增大而减小的一次函数关系式: .(填上一个答案即可)



