九年级(初三)数学：上学期上册　　 下学期下册

九年级(初三)数学下学期下册试题

已知抛物线y=ax2+bx+c与x轴交于A（1，0），B（3，0），与y轴交于C（0，﹣2），顶点为D，点E的坐标为（0，﹣1），该抛物线于BE交于另一点F，连接BC

（1）求该抛物线的解析式；
（2）若点H（1，y）在BC上，连接FH，求△FHB的面积；
（3）一动点M从点D出发，以每秒1个单位的速度沿平行于y轴方向向上运动，连接OM，BM，设运动时间为t秒（t＞0），点M在运动过程中，当t为何值时，∠OMB=90°？
（4）在x轴上方的抛物线上，是否存在点P，使得∠PBF被BA平分？若存在，直接写出点P的坐标；若不存在，请说明利由．

已知反比例函数y= 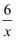$\text{[math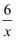]}$ ，当1＜x＜3时，y的最小整数值是（　　）

A . 3 B . 4 C . 5 D . 6

如图，平面直角坐标系中，正方形ABCD的顶点B，C在x轴上，反比例函数 $\text{[math]}$ （x>0）的图象经过点A（1，3），交CD于点E.

（1）求该反比例函数的解析式：
（2）求△BCE的面积.

如图，某轮船以每小时30海里的速度向正东方向航行，上午8：00，测得小岛 $\text{[math]}$ 在轮船的北偏东45°方向；上午10：00，测得小岛 $\text{[math]}$ 在轮船的北偏西30°方向，则轮船在航行中离小岛最近的距离约为海里（结果保留根号）.

下列结论中正确的是（）

A . 有两条边长是3和4的两个直角三角形相似 B . 一个角对应相等的两个等腰三角形相似 C . 两边对应成比例且一个角对应相等的两个三角形相似 D . 有一个角为60°的两个等腰三角形相似

计算： $\text{[math]}$

已知反比例函数y= $\text{[math]}$ ，当1＜x＜3时，y的取值范围是（　　）

A . 0＜y＜l B . 1＜y＜2 C . 2＜y＜6 D . y＞6

下面关于两个图形相似的判断：①两个等腰三角形相似；②两个等边三角形相似；③两个等腰直角三角形相似；④两个正方形相似；⑤两个等腰梯形相似．其中正确的个数是（）

A . 1 B . 2 C . 3 D . 4

△ABC中，已知∠A=30°，AB=2，AC=4，则△ABC的面积是（　　）

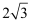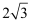A . $\text{[math]}$ B . 4 C . $\text{[math]}$ D . 2

如图是由6个相同的正方形拼成的图形，请你将其中一个正方形移动到合适的位置，使它与另5个正方形能拼成一个正方体的表面展开图．（请在图中将要移动的那个正方形涂黑，并画出移动后的正方形）．

在△ABC中，AB=6cm，点P在AB上，且∠ACP=∠B，若点P是AB的三等分点，则AC的长是．

如图是一个台阶形的零件，两个台阶的高度和宽度都相等，则它的三视图是（）

A .

B .

C .

D .

用计算器求下列格式的值（结果精确到0.0001）．

（1）tan63°27′；

（2）cos18°59′27″；

（3）sin67°38′24″．

如图，在平面直角坐标系中，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，以 $\text{[math]}$ 为直角边作 $\text{[math]}$ ，并使 $\text{[math]}$ ，再以 $\text{[math]}$ 为直角边作 $\text{[math]}$ ，并使 $\text{[math]}$ ，再以 $\text{[math]}$ 为直角边作 $\text{[math]}$ ，并使 $\text{[math]}$ …按此规律进行下去，则点 $\text{[math]}$ 的坐标为.

如图，以点 $\text{[math]}$ 为位似中心，把 $\text{[math]}$ 放大2倍得到 $\text{[math]}$ '，① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三点在同一直线上.则以上四种说法正确的是．