九年级(初三)数学下学期下册试题
如图,已知△ABC内接于⊙O,AB=AC=8,将弧AB沿弦AB翻折后恰好经过弦AC的中点D,则弦BC的长为 ,⊙O的半径为 .

如图,矩形的长和宽分别是4和3,等腰三角形的底和高分别是3和4,如果此三角形的底和矩形的宽重合,并且沿矩形两条宽的中点所在的直线自右向左匀速运动至等腰三角形的底与另一宽重合.设矩形与等腰三角形重叠部分(阴影部分)的面积为y,重叠部分图形的高为x,那么y关于x的函数图象大致应为( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,点A在双曲线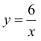 上,
上, ,过A作
,过A作 ,垂足为C,OA的垂直平分线交OC于B,且,则
,垂足为C,OA的垂直平分线交OC于B,且,则 的周长为( )
的周长为( )

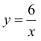 上,
上, ,过A作
,过A作 ,垂足为C,OA的垂直平分线交OC于B,且,则
,垂足为C,OA的垂直平分线交OC于B,且,则 的周长为( )
的周长为( )
A . 6.5
B . 5.5
C . 5
D . 4
如图,△ABC中,D、E两点分别在BC、AC上,且AD平分∠BAC,若∠ABE=∠C,BE与AD相交于点F.则图中相似三角形的对数是( )

A . 1
B . 2
C . 3
D . 4
一个圆锥的侧面积是底面积的4倍,则圆锥侧面展开图的扇形的圆心角是( )
A . 60°
B . 90°
C . 120°
D . 180°
已知四边形ABCD与四边形A1B1C1D1相似,且A1B1:B1C1:C1D1:D1A1=7:8:11:14,若四边形ABCD的周长为40,求四边形ABCD各边的长.
 位似于
位似于  ,它们的周长比为
,它们的周长比为  ,已知位似中心O到A的距离为3,那么O到D的距离为( )
,已知位似中心O到A的距离为3,那么O到D的距离为( )
A . 4
B . 4.5
C . 6
D . 9
如图,两条宽度都是1的纸条,交叉重叠放在一起,且夹角为α,则重叠部分的面积为( )


A .  B .
B .  C . tanα
D . 1
C . tanα
D . 1
 B .
B .  C . tanα
D . 1
C . tanα
D . 1
已知反比例函数  ,在x>0时,y随x的增大而增大,则k的取值范围是
,在x>0时,y随x的增大而增大,则k的取值范围是
 ,在x>0时,y随x的增大而增大,则k的取值范围是
,在x>0时,y随x的增大而增大,则k的取值范围是
如图,在▱ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.

-
(1) 求证:四边形ABEF是菱形;
-
(2) 若AB=4,AD=6,∠ABC=60°,求tan∠ADP的值.
小明家所在居民楼的对面有一座大厦AB=74米,为测量这座居民楼与大厦之间的水平距离CD的长度,小明从自己家的窗户C处测得∠DCA=37°,∠DCB=48°(DC平行于地面).求小明家所在居民楼与大厦的距离CD的长度.
(参考数据:sin37°  ,tan37°
,tan37°  ,sin48°
,sin48°  ,tan48°
,tan48°  )
)

如图,在平面直角坐标系中,直线 分别与反比例函数
分别与反比例函数 的图象交于点A、B,与y轴交于点C,若
的图象交于点A、B,与y轴交于点C,若 , 则m的值可以是( )
, 则m的值可以是( )
 分别与反比例函数
分别与反比例函数 的图象交于点A、B,与y轴交于点C,若
的图象交于点A、B,与y轴交于点C,若 , 则m的值可以是( )
, 则m的值可以是( )

A . 2.1
B . -1.8
C . -2.1
D . -3.4
计算: 

在下面四个立体图形中,从左面看与从正面看所得到的平面图形不相同的是( )
A .  正方体
B .
正方体
B .  长方体
C .
长方体
C .  球
D .
球
D .  圆锥
圆锥
 正方体
B .
正方体
B .  球
D .
球
D .  圆锥
圆锥
△ABC中,∠A , ∠B都是锐角,且sinA=  ,cosB=
,cosB=  ,则△ABC的形状是( )
,则△ABC的形状是( )
 ,cosB=
,cosB=  ,则△ABC的形状是( )
,则△ABC的形状是( )
A . 直角三角形
B . 钝角三角形
C . 锐角三角形
D . 锐角三角形或钝角三角形
如图,在△ABC中,AC=4,CD=2,BC=8,点D在BC边上.

-
(1) 判断△ABC与△DAC是否相似?请说明理由.
-
(2) 当AD=3时,求AB的长.
如图,  中,
中,  ,
,  ,点D、E分别在AC、CB上,
,点D、E分别在AC、CB上,  ,AE与BD交于点O,连OC,则OC的长是.
,AE与BD交于点O,连OC,则OC的长是.

画出下列几何体的三视图

如图1,抛物线y=  x2+bx+c与x轴负半轴交于点A,与x轴正半轴交于点B,与y轴的负半轴交于点C,OC=OB=10。
x2+bx+c与x轴负半轴交于点A,与x轴正半轴交于点B,与y轴的负半轴交于点C,OC=OB=10。
 x2+bx+c与x轴负半轴交于点A,与x轴正半轴交于点B,与y轴的负半轴交于点C,OC=OB=10。
x2+bx+c与x轴负半轴交于点A,与x轴正半轴交于点B,与y轴的负半轴交于点C,OC=OB=10。

-
(1) 求抛物线的表达式;
-
(2) 点P、Q在第四象限内抛物线上,点P在点Q下方,连接CP,CQ,∠OCP+∠OCQ=180°,设点Q的横坐标为m,点P的横坐标为n,求m与n的函数关系式;
-
(3) 如图2,在(2)的条件下,连接AP交CO于点D,过点Q作QE⊥AB于点E,连接BQ,DE,是否存在点P,使∠AED=2∠EQB,若存在,求出点P的坐标;若不存在,请说明理由。
如图,在⊙O中,AB为直径,P为AB上一点,PA=1,PB=m(m为常数,且m>0).过点P的弦CD⊥AB,Q为  上一动点(与点B不重合),AH⊥QD,垂足为H.连接AD、BQ.
上一动点(与点B不重合),AH⊥QD,垂足为H.连接AD、BQ.
 上一动点(与点B不重合),AH⊥QD,垂足为H.连接AD、BQ.
上一动点(与点B不重合),AH⊥QD,垂足为H.连接AD、BQ. 
-
(1) 若m=3.
①求证:∠OAD=60°;
②求
 的值;
的值; -
(2) 用含m的代数式表示
 ,请直接写出结果;
,请直接写出结果;
-
(3) 存在一个大小确定的⊙O,对于点Q的任意位置,都有BQ2﹣2DH2+PB2的值是一个定值,求此时∠Q的度数.
最近更新
- —How can I get to Guangzhou within five hours? —There
- 小明利用如图所示的电路来测定小灯泡的电功率.已知小灯泡的额定电压为2.5V,所用的滑动变阻器标有“15Ω、1.5 A”字
- E,F是等腰直角斜边AB上的三等分点,则A. B. C. D.
- 下列句子标点符号的使用,正确的一句是A、我们没有想到的是:马加爵的泪水竟然远比死者的鲜血更让人觉得沉重;而他的忏悔与自白
- 2015年9月19日第九届合肥文博会开幕.开幕前夕,我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销.经过
- 货币在执行价值尺度的职能时,货币是() A、价值不变的特殊商品 B、现实的货币 C、一种价值符号 D、想象的货币
- 19世纪初,英国有钱人以坐蒸汽轮船游览伦敦泰晤士河为时尚,而呼啸而过的火车也取代了旧时的马车。实现这一切的关键在于 A.
- 假药亮菌甲素注射液,其溶剂二甘醇进入人体后导致急性肾衰竭,临床上用血液透析治疗。血透机工作原理如图,所用的透析管膜应具有
- 短周期主族元素A、B、C、D的原子序数依次增大,其中C为金属元素,C的最外层电子数和A相等;C、D两元素原子的质子数之和
- 工业上利用下列反应:TiO2+SiSiO2+Ti,制取钛,该反应中的氧化剂是 A.TiO2
- 我国东部季风区气候夏季共同的特点是( ) A.炎热干燥 B.雨热同期 C.低温少
- 下列句子中有语病的一项是( )(2分) A.阅读优秀的文学作品,既能增长知识,又能丰富情感。 B.“春
- 如图所示,在一根水平直杆上套着a、b两个轻质小环,在环下用两根等长的细轻绳拴着一个重物。把两环分开放置,静止时,杆对a环
- 将质量为0.5kg的小球以20m/s的初速度竖直向上抛出.不计空气阻力,取10m/s2.以下判断正确的是A.小球从抛
- 唯物辩证法与形而上学的根本分歧是( ) A.联系的观点与孤立的观点的对立 B.发展的观点与静止的观点的对立 C.全面的
- — Could you tell me ________? — “Rome was not builtin a day.
- 褶皱全是压力作用形成,断层全是由拉力作用形成的。
- 化学就在我们身边,现有①稀盐酸;②小苏打;③熟石灰;④石墨;⑤甲烷;⑥生石灰中,从中选择适当的物质按下列要求填空(填序号
- 18.阅读下面的材料,根据要求写一篇不少于800字的文章。 有人在飞机上发现这样一个现象:同样是30岁到40岁年纪的旅客
- 有人设计了锌溴可充式电池并给出充电与放电的化学方程式Zn + Br2 ==== Zn2+ + 2Br-, 但是他忘记标出



