九年级(初三)数学下学期下册试题
若圆锥的底面半径为3cm,高是4cm,则它的侧面展开图的面积为.
邓州杏山地质公园位于河南省邓州市西南约50公里处,紧邻丹江口水库南水北调渠首,面积32.5平方公里.公园地质景观及自然景观为原始状态,是一座集岩溶地貌、典型底层剖面和地质构造为主,水体为辅、人文和生态相互辉映的综合性公园(如图1).双休日期间,小明携带测量工具随妈妈到杏山地质公园游览,为测量杏山主峰的高度,如图2,小明在坡角为  的斜坡C处测得峰顶A的仰角为
的斜坡C处测得峰顶A的仰角为  ,沿斜坡CD走
,沿斜坡CD走  到平坦地面上点D处,测得峰顶A的仰角为
到平坦地面上点D处,测得峰顶A的仰角为  .
.
 的斜坡C处测得峰顶A的仰角为
的斜坡C处测得峰顶A的仰角为  ,沿斜坡CD走
,沿斜坡CD走  到平坦地面上点D处,测得峰顶A的仰角为
到平坦地面上点D处,测得峰顶A的仰角为  .
. 

-
(1) 求主峰到地面的高度AB(结果保留整数,参考数据
 )
)
-
(2) 妈妈借助手机某项功能得到杏山主峰海拔为
 ,所测水平地面的海拔为
,所测水平地面的海拔为  ,请你算出小明测量主峰高度的误差,并帮助他提一条减小误差的方法.
,请你算出小明测量主峰高度的误差,并帮助他提一条减小误差的方法.
如图,过双曲线y=  上的A、B两点分别向x轴、y轴作垂线,垂足分别为C、E、D、F,AC、BF相交于点G,矩形ADFG和矩形BECG的面积分别为S1、S2 , 若S阴影=1,则S1+S2=.
上的A、B两点分别向x轴、y轴作垂线,垂足分别为C、E、D、F,AC、BF相交于点G,矩形ADFG和矩形BECG的面积分别为S1、S2 , 若S阴影=1,则S1+S2=.
 上的A、B两点分别向x轴、y轴作垂线,垂足分别为C、E、D、F,AC、BF相交于点G,矩形ADFG和矩形BECG的面积分别为S1、S2 , 若S阴影=1,则S1+S2=.
上的A、B两点分别向x轴、y轴作垂线,垂足分别为C、E、D、F,AC、BF相交于点G,矩形ADFG和矩形BECG的面积分别为S1、S2 , 若S阴影=1,则S1+S2=. 
如图,要测量某山的高度  ,小明先在山脚
,小明先在山脚  点测得山顶
点测得山顶  的仰角为
的仰角为  ,然后沿坡度为
,然后沿坡度为  的斜坡走100米到达
的斜坡走100米到达  点,在
点,在  点测得山顶
点测得山顶  的仰角为
的仰角为  ,求这座山的高度
,求这座山的高度  .(结果保留整数)(参考数据:
.(结果保留整数)(参考数据:  ,
, 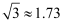 )
)
 ,小明先在山脚
,小明先在山脚  点测得山顶
点测得山顶  的仰角为
的仰角为  ,然后沿坡度为
,然后沿坡度为  的斜坡走100米到达
的斜坡走100米到达  点,在
点,在  点测得山顶
点测得山顶  的仰角为
的仰角为  ,求这座山的高度
,求这座山的高度  .(结果保留整数)(参考数据:
.(结果保留整数)(参考数据:  ,
, 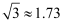 )
) 
如图是一个几何体的主视图,则该几何体是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图所示的几何体的俯视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
由5个大小相同的正方体组成的几何体如图所示,从正面看到的图形是( )

A .  B .
B .  C .
C .  D .
D . 
计算tan1°•tan2°•tan3°•…•tan88°•tan89°= .
阅读材料:
关于三角函数还有如下的公式:
Sin(α±β)=sinαcosβ±cosαsinβ
tan(α±β)= 
利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值,
例:tan15°=tan(45°﹣30°)
= 
= 
= 
根据以上阅读材料,请选择适当的公式解答下面的问题
-
(1) 计算sin15°;
-
(2) 我县体育场有一移动公司的信号塔,小明想利用所学的数学知识来测量该塔的高度,小华站在离塔底A距离7米的C处,测得塔顶的仰角为75°,小华的眼睛离地面的距离DC为1.62米,请帮助小华求出该信号塔的高度.(精确到0.1米,参考数据:
 ≈1.414)
≈1.414) 
定义一个新的运算:a⊕b= , 则运算x⊕2的最小值为( )
, 则运算x⊕2的最小值为( )
 , 则运算x⊕2的最小值为( )
, 则运算x⊕2的最小值为( )
A . ﹣3
B . ﹣2
C . 2
D . 3
如图是反比例函数y= 的图象,下列说法正确的是( )
的图象,下列说法正确的是( )

A . 常数m<﹣1
B . 在每个象限内,y随x的增大而增大
C . 若A(﹣1,h),B(2,k)在图象上,则h<k
D . 若P(x,y)在图象上,则P′(﹣x,y)也在图象上
如图,A.B是双曲线y=  上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若△ADO的面积为1,D为OB的中点,则k的值为.
上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若△ADO的面积为1,D为OB的中点,则k的值为.
 上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若△ADO的面积为1,D为OB的中点,则k的值为.
上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若△ADO的面积为1,D为OB的中点,则k的值为.
如图,一位测量人员,要测量池塘的宽度  的长,他过
的长,他过  两点画两条相交于点
两点画两条相交于点  的射线,在射线上取两点
的射线,在射线上取两点  ,使
,使  ,若测得
,若测得  米,他能求出
米,他能求出  之间的距离吗?若能,请你帮他算出来;若不能,请你帮他设计一个可行方案.
之间的距离吗?若能,请你帮他算出来;若不能,请你帮他设计一个可行方案.
 的长,他过
的长,他过  两点画两条相交于点
两点画两条相交于点  的射线,在射线上取两点
的射线,在射线上取两点  ,使
,使  ,若测得
,若测得  米,他能求出
米,他能求出  之间的距离吗?若能,请你帮他算出来;若不能,请你帮他设计一个可行方案.
之间的距离吗?若能,请你帮他算出来;若不能,请你帮他设计一个可行方案.
计算:2sin60°+tan45°=.
下面两个图形一定相似的是( )
A . 两个等腰三角形
B . 矩形
C . 菱形
D . 正方形
如图,在反比例函数y=  的图象上有一动点
的图象上有一动点  ,连接
,连接 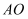 并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数
并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数  的图象上运动,
的图象上运动,  ,则关于
,则关于  的解为.
的解为.

如图,在6×8的正方形网格中,共有48个边长为1 的小正方形.A,B,C,D,E都是正方形网格上的格点.连接DE,DB交AC于点P、Q,则PQ的值是( )

A .  B .
B . 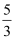 C .
C .  D .
D . 
 B .
B . 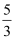 C .
C .  D .
D . 
如图,已知矩形OABC中,OA=2,AB=4,双曲线  (k>0)与矩形两边AB、BC分别交于E、F.
(k>0)与矩形两边AB、BC分别交于E、F.

-
(1) 若E是AB的中点,求F点的坐标;
-
(2) 若将△BEF沿直线EF对折,B点落在x轴上的D点,作EG⊥OC,垂足为G,证明△EGD∽△DCF,并求k的值.
一直角三角形中,斜边与一直角边的比是13:12,最小角为α,则sinα=,cosα=,tanα=.
如图,在 中,
中, ,
,  ,
,  ,
,  , 点
, 点 在
在 上运动,连接
上运动,连接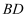 , 把
, 把 沿
沿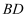 折叠得到
折叠得到 ,
,  交
交 于点
于点 ,
,  , 则图中阴影部分的面积是( )
, 则图中阴影部分的面积是( )
 中,
中, ,
,  ,
,  ,
,  , 点
, 点 在
在 上运动,连接
上运动,连接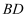 , 把
, 把 沿
沿 折叠得到
折叠得到 ,
,  交
交 于点
于点 ,
,  , 则图中阴影部分的面积是( )
, 则图中阴影部分的面积是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
最近更新
- (08年南海市模拟)(16分)如图所示,光滑水平面上有A、B、C三个物块,其质量分别为mA = 2.0kg,mB = 1
- 阅读下面的文字,完成下题。 由青蒿素产业化带来的双创启示 草容 屠呦呦荣获诺奖,是对她个人的奖励,也是对青蒿素产业化的褒
- 已知函数的定义域,部分对应值如下表,的导函数的图像如图所示。x ﹣1 0 2 4 5 f(x) 1 2 1 2 1
- 自来水消毒过程中通常会发生如下化学反应,其反应的微观过程可用下图表示: ( 表示氯原子, 表示氧原子, 表示氢
- -- What do you think of David ? -- There are some thing
- 2009年4月以来,从墨西哥蔓延开来的流感,最初被诊断为猪流感。后来,世界卫生组织等权威机构研究发现,这种流感病毒实际包
- 下列叙述正确的是() A.单体的质量之和一定等于所生成的高聚物的质量 B.单体为一种物质时,则单体只能发生加聚反应 C.
- 甲、乙、丙、丁四名同学在一次投掷实心球训练中,在相同条件下各投掷10次,他们成绩的平均数与方差如下表:甲 乙 丙 丁 平
- 自养型微生物与异养型微生物的培养基的主要差别是 A.碳源 B.氮源 C. 碳源和氮源
- Jumping out of ____airplane at ten thousand feet is quite __
- 下图是“某国人口自然增长率随时间变化示意图”目前人口增长特点与②时期相符合的国家是
- 比较阅读甲、乙两个文段,完成1-6题 【甲】故天将降大任于是人也,必先苦其心志,劳其筋骨,饿其体肤,空乏其身,行拂乱其所
- —Can you give some advice on what I said just now? ---Sorry.
- 孟德尔在研究豌豆一对相对性状的遗传时,设计的对现象解释的验证实验称为( ) A.测交 B.杂交 C.自交 D.正交
- 取等质量的A、B金属,分别投入溶质质量分数相同的足量的盐酸中,生成氢气的质量(m) 与时间(t)的关系如图。(已知A、B
- 关于化学键的下列叙述中正确的是( )A.离子化合物不可能含共价键 B.共价化合物可能含离子键C.离
- 26.—You look quite tired. —I __________ the project here in
- 如图,直线与x轴交于点A,与y轴交于点B,点C是射线BA上的一个动点. ⑴求sin∠OAB的值; ⑵当△OAC是以OA为
- 以乙烯为原料合成化合物C的流程如下所示:(1)反应①⑤的反应类型分别为▲ 、▲ 。 (2)写出反应③和⑤的化学方程式
- (2009年广东理基)与植物顶端优势有关的植物激素是() A.生长素



