九年级(初三)数学下学期下册试题
某公司大门出口处有一自动感应栏杆,点A是栏杆转动的支点,当车辆经过时,栏杆AE会自动升起,某天早上,栏杆发生故障,在某个位置突然卡住,这时测得栏杆升起的角度∠BAE=127°,已知AB⊥BC,支架AB高1.2米,大门BC打开的宽度为2米,这时一辆长宽高分别为(4600mm、1700mm、1400mm)的汽车能否顺利通过?(栏杆宽度,汽车反光镜忽略不计,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.)

计算: 

如图,在矩形ABCD中,把∠A沿DF折叠,点A恰好落在矩形的对称中心E处,则tan∠ADF=

如图,以原点O为位似中心,把△OAB放大后得到△OCD,求△OAB与△OCD的相似比.

在Rt△ABC中,如果  ,那么
,那么  表示
表示 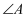 的( )
的( )
 ,那么
,那么  表示
表示 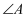 的( )
的( )
A . 正弦
B . 正切
C . 余弦
D . 余切
如图,直线  与x轴交于点M,与y轴交于点A,过点A作
与x轴交于点M,与y轴交于点A,过点A作  ,交x轴于点B,以AB为边在AB的右侧作正方形ABCA1 , 延长A1C交x轴于点B1 , 以A1B1为边在A1B1的右侧作正方形A1B1C1A2…按照此规律继续作下去,再将每个正方形分割成四个全等的直角三角形和一个小正方形,每个小正方形的每条边都与其中的一条坐标轴平行,正方形ABCA1 , A1B1C1A2 , …,
,交x轴于点B,以AB为边在AB的右侧作正方形ABCA1 , 延长A1C交x轴于点B1 , 以A1B1为边在A1B1的右侧作正方形A1B1C1A2…按照此规律继续作下去,再将每个正方形分割成四个全等的直角三角形和一个小正方形,每个小正方形的每条边都与其中的一条坐标轴平行,正方形ABCA1 , A1B1C1A2 , …,  中的阴影部分的面积分别为S1 , S2 , …,Sn , 则Sn可表示为.
中的阴影部分的面积分别为S1 , S2 , …,Sn , 则Sn可表示为.
 与x轴交于点M,与y轴交于点A,过点A作
与x轴交于点M,与y轴交于点A,过点A作  ,交x轴于点B,以AB为边在AB的右侧作正方形ABCA1 , 延长A1C交x轴于点B1 , 以A1B1为边在A1B1的右侧作正方形A1B1C1A2…按照此规律继续作下去,再将每个正方形分割成四个全等的直角三角形和一个小正方形,每个小正方形的每条边都与其中的一条坐标轴平行,正方形ABCA1 , A1B1C1A2 , …,
,交x轴于点B,以AB为边在AB的右侧作正方形ABCA1 , 延长A1C交x轴于点B1 , 以A1B1为边在A1B1的右侧作正方形A1B1C1A2…按照此规律继续作下去,再将每个正方形分割成四个全等的直角三角形和一个小正方形,每个小正方形的每条边都与其中的一条坐标轴平行,正方形ABCA1 , A1B1C1A2 , …,  中的阴影部分的面积分别为S1 , S2 , …,Sn , 则Sn可表示为.
中的阴影部分的面积分别为S1 , S2 , …,Sn , 则Sn可表示为. 
如图,D是  边
边  延长线上一点,添加一个条件后,仍然不能使
延长线上一点,添加一个条件后,仍然不能使  的是( )
的是( )
 边
边  延长线上一点,添加一个条件后,仍然不能使
延长线上一点,添加一个条件后,仍然不能使  的是( )
的是( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若双曲线  位于第二、四象限,则k的取值范围是( )
位于第二、四象限,则k的取值范围是( )
 位于第二、四象限,则k的取值范围是( )
位于第二、四象限,则k的取值范围是( )
A . k<1
B . k≥1
C . k>1
D . k≠1
如图,司机发现前方十字路口有红灯,立即减速,在B处踩刹车,此时测得司机看正前方人行道的边缘上A处的俯角为30°,汽车滑行到达C处时停车,此时测得司机看A处的俯角为60°.已知汽车刹车后滑行距离BC的长度为3米,求司机眼睛P与地面的距离.(结果保留根号)

如图,DE∥FG∥BC,若DB=4FB,则EG与GC的关系是( )

A . EG=4GC
B . EG=3GC
C . EG=  GC
D . EG=2GC
GC
D . EG=2GC
 GC
D . EG=2GC
GC
D . EG=2GC
一张圆形纸片裁剪后正好能做三个一样的无底圆锥纸帽(无余料,接缝不计),若圆锥的高为4cm,则每个圆锥的侧面积是.
若圆锥的侧面展开图是一个半径为a的半圆,则圆锥的高为( )
A . a
B .  a
C . 3a
D .
a
C . 3a
D .  a
a
 a
C . 3a
D .
a
C . 3a
D .  a
a
如图1是一款可调节儿童书桌椅,图2是它的示意图.座位  宽度为
宽度为  其竖直高度
其竖直高度  为
为  为桌面板
为桌面板  的中点,某儿童坐在座位上眼睛F距离水平地面的高度为
的中点,某儿童坐在座位上眼睛F距离水平地面的高度为  研究表明:当桌面板与竖直方向夹角
研究表明:当桌面板与竖直方向夹角  视线
视线  与桌面板所呈锐角
与桌面板所呈锐角  时最舒适,问此时OD高度应调节为多少?(参考数据:
时最舒适,问此时OD高度应调节为多少?(参考数据: 
 ,
,  结果精确到
结果精确到  )
)
 宽度为
宽度为  其竖直高度
其竖直高度  为
为  为桌面板
为桌面板  的中点,某儿童坐在座位上眼睛F距离水平地面的高度为
的中点,某儿童坐在座位上眼睛F距离水平地面的高度为  研究表明:当桌面板与竖直方向夹角
研究表明:当桌面板与竖直方向夹角  视线
视线  与桌面板所呈锐角
与桌面板所呈锐角  时最舒适,问此时OD高度应调节为多少?(参考数据:
时最舒适,问此时OD高度应调节为多少?(参考数据: 
 ,
,  结果精确到
结果精确到  )
) 
如图,∠A=∠B=90°,AB=7,AD=2,BC=3,在边AB上取点P,使得△PAD与△PBC相似,则这样的P点共有( )

A . 1个
B . 2个
C . 3个
D . 4个
计算  .
.
 .
.
计算:
-
(1) 2sin60°tan30°+cos230°-tan45°.
-
(2) (2x﹣3)2﹣2(2x﹣3)﹣3=0.
计算题
-
(1) 计算:(cos230°+sin230°)×tan60°
-
(2) 解方程:x2﹣2
 x﹣1=0.
x﹣1=0.
如图,在四边形ABCD中,DC∥AB,AD=5,CD=3,sinA=sinB=  ,动点P自A点出发,沿着边AB向点B匀速运动,同时动点Q自点A出发,沿着边AD﹣DC﹣CB匀速运动,速度均为每秒1个单位,当其中一个动点到达终点时,它们同时停止运动,设点P运动t(秒)时,△APQ的面积为s,则s关于t的函数图象是( )
,动点P自A点出发,沿着边AB向点B匀速运动,同时动点Q自点A出发,沿着边AD﹣DC﹣CB匀速运动,速度均为每秒1个单位,当其中一个动点到达终点时,它们同时停止运动,设点P运动t(秒)时,△APQ的面积为s,则s关于t的函数图象是( )
 ,动点P自A点出发,沿着边AB向点B匀速运动,同时动点Q自点A出发,沿着边AD﹣DC﹣CB匀速运动,速度均为每秒1个单位,当其中一个动点到达终点时,它们同时停止运动,设点P运动t(秒)时,△APQ的面积为s,则s关于t的函数图象是( )
,动点P自A点出发,沿着边AB向点B匀速运动,同时动点Q自点A出发,沿着边AD﹣DC﹣CB匀速运动,速度均为每秒1个单位,当其中一个动点到达终点时,它们同时停止运动,设点P运动t(秒)时,△APQ的面积为s,则s关于t的函数图象是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
圆锥底面半径为  ,母线长为
,母线长为 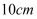 ,则圆锥的侧面积为cm2 .
,则圆锥的侧面积为cm2 .
 ,母线长为
,母线长为 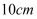 ,则圆锥的侧面积为cm2 .
,则圆锥的侧面积为cm2 .
如图是由10个大小相同的小立方体搭建的几何体,其中每个小立方体的棱长为1厘米.

-
(1) 请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图;
-
(2) 若现在你手头还有一些相同的小正方体,如果保持俯视图和左视图不变,最多可以再添加个小正方体(直接填空).
最近更新
- 如图为恩格尔曼为研究光合作用所设计的实验及其结果,对此分析不正确的是()A.图示实验环境不能看做一个小型生态系统 B.水
- Don't ______ the windows open---it's inviting thieves to ent
- 下列运算中,结果是的是( ) A. B. C. D.
- 用配方法解方程,下列配方正确的是( ) A、 B、 C、 D、
- 按要求默写。(共8小题,每题1分,共8分)【小题1】____________________ ,中间小谢又清发。
- 具有下列电子排布式的原子中,半径最大的为( )A.1s22s22p63s1
- 右图是某短大衣标签的部分内容,下列有关认识不正确的是 A. 短大衣是由两种材料制成的 B. 羊毛和涤纶均属于有机高分子
- 下图为近代“帽业专家”盛锡福帽店的产品商标。某历史文献有如下记载:“失去辫子,人们一时难以适应这种变化,于是,时兴起戴帽
- . The boy wanted to ride his bicycle in the street, but his
- 函数的定义域为:
- 18世纪的法国爆发了世界瞩目的启蒙运动,启蒙大师们高举自由、平等、人权和理性的旗帜,向封建专制制度和宗教神学发动了猛烈的
- 已知f(x)=a1x+a2x2+…+anxn(n为正偶数)且{an}为等差数列,f(1)=n2,f(-1)=n,试比较与
- 根据下列实验操作和现象所得到的结论正确的是( ) 选项 实验操作和现象 结论 A 室温下,向明矾溶液中加入足量的浓
- 如图7所示,闭合开关S,当滑动变阻器的滑片P向左移动时,下列说法正确的是
- 近几年,我国北京、上海、广州等地引进了十多台“γ刀”,成为治疗脑肿瘤的最佳仪器.用“γ刀”治疗不用麻醉,时间短,效果佳,
- (2010萧山).(8分)为创建全国“环保节能模范城市”,新建的小区将普遍安装太阳能路灯。如图甲所示是某型号太阳能路灯,
- 25℃时,若体积为Va、pH=a的某一元强酸与体积Vb、pH=b的某一元强碱混合,恰好中和,且已知Va<Vb和a=
- 在家中,小明取少量的下列物质分别放入水中,充分搅拌,其中能形成溶液的是 A.蔗糖 B.面粉
- 下列各种反射中,与其他反射不属于同一类型的是( ) A.马戏团的小狗做算术 B.鹦鹉对
- 一物体受到三个共点力的作用,它们的大小分别为F1=3N、F2=5N、F3=10N,则它们的合力大小不可能是( )(A)



