下列形状能和正八边形组合在起进行密铺的是（  ）

如图，点E是四边形ABCD的对角线BD上一点，且∠BAC＝∠BDC＝∠DAE.

①试说明BE·AD＝CD·AE；

如图△ABC中，∠C=90°，AC=8cm，AB的垂直平分线MN交AC于D，连接BD，若cos∠BDC= ，则BC的长为．

如图，由三个相同小立方体组成的几何图形的左视图是(     )

某几何体的三视图如图，则该几何体是（   ）

如图，将一个圆柱体放置在长方体上，其中圆柱体的底面直径与长方体的宽相平，则该几何体的左视图是（　　）

下列线段中，能成比例的是（   ）

如图是一个正方体的表面展开图，则这个正方体是（   ）

如图，矩形ABCD是一道门的门框，将一条长为1米的木棒的一端放在门框AB上的点E处，将木棒靠在左边门框AD上时，另一端落在点G处，保持一端在点E不动，将木棒靠在右边门框BC时，另一端落在点F处．测得∠AGE=30°，∠EFB=45°，则与门框的宽度AB最接近的长度为(    )(参考： ≈1.414， ≈1.732)

 

如图，在平面直角坐标系xOy中，△OAB如图放置，点A的坐标为（3，4），点P是AB边上的一点，过点P的反比例函数 与OA边交于点E，连接OP．

如图，在Rt△ABC中，∠C=90°，∠B=30°，AB=8，则BC的长是（  ）

点D、E分别在等边△ABC的边AB、BC上，将△BDE沿直线DE翻折，使点B落在B₁处，DB₁、EB₁分别交边AC于点F、G．若∠ADF=80°，则∠CGE=．

如图，直线 ， 被三条平行线所截，若 ， ， ，则 的长为（  ）

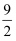
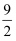
制作一种产品，需先将材料加热达到60℃后，再进行操作．设该材料温度为 （℃），从加热开始计算的时间为 （分钟）．据了解，该材料加热时，温度 与时间 成一次函数关系；停止加热进行操作时，温度 与时间 成反比例关系（如图8所示）．已知该材料在操作加工前的温度为15℃，加热5分钟后温度达到60℃．

如图是某超市地下停车场入口的设计图，请根据图中数据计算CE的长度．（结果保留小数点后两位；参考数据：sin22°=0.3746，cos22°=0.9272，tan22°=0.4040）

将一个棱长为1的正方体水平放于桌面（始终保持正方体的一个面落在桌面上），则该正方体正视图面积的最大值为（  ）

计算： ．

如图，身高1.8米的小石从一盏路灯下B处向前走了8米到达点C处时，发现自己在地面上的影子CE长是2米，则路灯的高AB为米.

如图，一棵松树AB挺立在斜坡CB的顶端，斜坡CB长为52米，坡度为i＝12：5，小张从与点C相距60米的点D处向上爬12米到达观景台DE的顶端点E，在此测得松树顶端点A的仰角为39°，则松树的高度AB约为（       ）（参考数据：sin39°≈0.63，cos39°≈0.78，tan39°≈0.81）

如图，已知Rt△ABC中，∠C=90°，BC=3，AC=4，则sinA的值为（      ）